Contrainte thermique 02 : liaison quasi rigide et deux treillis

Déterminez les contraintes thermiques qui se développent lorsque la température d'un membre augmente.

Description du cas

Une liaison quasi-rigide pivote autour d'un trou à son extrémité droite. Le lien se trouve au-dessus d'une tige de laiton cylindrique. Une tige d'acier cylindrique s'ancre vers le bas à gauche du segment. La température de la tige du laiton est augmentée de 20 °C (température sans contrainte de l'ensemble) à 50 °C. L'expansion thermique résultante entraîne une contrainte de traction dans la tige de maintien en acier. La tige de laiton n'étant pas libre de s'étendre sans entrave, une contrainte de compression axiale se développe dans ce cas. Nous allons comparer cette contrainte axiale à la solution théorique.

Les éléments rigides ne sont pas disponibles dans le type d'analyse en question. Par conséquent, le comportement quasi rigide est obtenu en rendant la liaison relativement grande et en réglant la rigidité du matériau sur la valeur maximale prise en charge. Dans le schéma qui suit, toutes les cotes sont en millimètres.

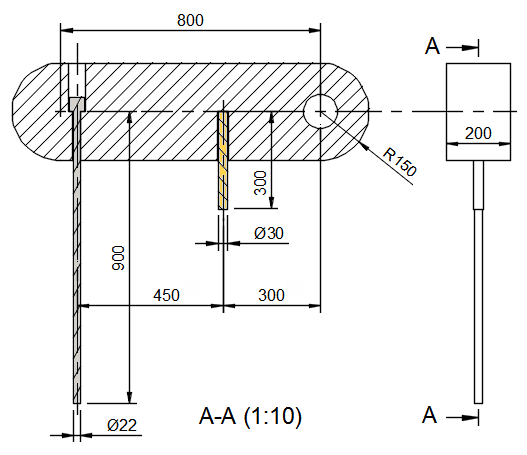
diagramme de contrainte thermique

Cotes (mm)

Lien : 1100 x 300 x 200 au total
Tige de laiton : 30 de diamètre x 300 de long
Tige d'acier : 22 de diamètre x 900 de long (sans la tête)

Type et paramètres de l'étude

Type d'étude : contrainte thermique
Température de référence sans contrainte : 20° C

Paramètres de maillage

Type de maillage = Solide, Tétraédrique
Taille du maillage = 30 mm, absolu
Ordre d'élément = parabolique
Affinement du maillage adaptatif : aucun
Contrôles du maillage local :
- Trou pivot dans le lien : taille de maillage de 15 mm
- Tige d'acier et faces de perçage associées dans le lien : taille de maillage de 5 mm
- Tige de laiton et faces de perçage associées dans le lien : taille de maillage de 7 mm

Propriétés du matériau

Propriété	Lien	Tige de laiton	Tige d'acier
Module d'élasticité [MPa]	1,3 x 10⁶	105,000	200,000
Coefficient de Poisson	0.3	0.31	0.3
Coefficient d'expansion thermique (/°C)	1,2 x 10^-5	1,88 x 10^-5	1,2 x 10^-5

Remarque : les coefficients de dilatation thermique de la tige et du lien en acier n'ont pas vraiment d'importance, car ces pièces ne subissent pas de changement de température.

Contraintes

Trou pivot dans le lien : contrainte de blocage (directions radiale et axiale)
Extrémité inférieure de la tige d'acier : fixe
Extrémité inférieure de la tige de laiton : contrainte Y uniquement
Face cylindrique de la tige de laiton : Contrainte de blocage (direction tangentielle uniquement)

Remarque : cette contrainte empêche la tige de tourner autour de n'importe quel axe, mais permet une croissance radiale due à une dilatation thermique. Par conséquent, la tige est statiquement stable et les contraintes thermiques artificielles ne sont pas provoquées par le schéma de contrainte.

Charges thermiques

Lien et tige d'acier (corps entier de chaque corps) : température appliquée de 20° C
Tige de laiton (corps entier) : température appliquée de 50° C

Paramètres de contact

Les trous dans la liaison des deux tiges sont dimensionnés pour le dégagement. Par conséquent, le contact se produit uniquement à deux emplacements :

Entre l'extrémité supérieure de la tige de laiton et l'extrémité du perçage borgne associé dans le lien.
Entre le bas de la tête de la tige d'acier et le bas du lamage associé dans le lien.

Les paramètres des deux jeux de composants en contact sont les suivants :

Type de contact : séparation
Type de pénétration : symétrique
Conductance thermique : 1 x 10-6 W / (m2·K)

Remarque : les trois corps reçoivent une température appliquée, afin de rendre la tige du laiton plus chaude et de garantir que les températures des deux autres pièces restent à leurs valeurs sans contrainte. Pour réduire le flux de chaleur à l'endroit où les composants se rencontrent, une conductance thermique nulle est souhaitable. Toutefois, une valeur de conductance nulle entraîne l'échec de la solution. Par conséquent, nous spécifions une valeur de conductance très petite.

Solution théorique

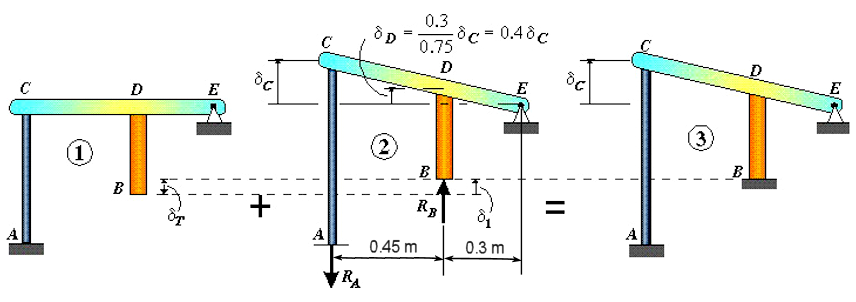
diagramme de la théorie des contraintes thermiques

En prenant en compte le diagramme précédent, nous avons les relations suivantes de la référence Beer and Johnston :

Σ = 0 RA * (0,75 m) - RB * (0,3 m) = 0 RA = 0,4 RB

Déformations

La méthode de superposition est utilisée. Lorsque l'élévation de la température du cylindre est supprimée, le point B descend sur une distance de déplacement. La réaction RB entraîne un déplacement δ1 de la même magnitude que δT afin que le déplacement final du point B soit égal à zéro.

En raison d'une augmentation de la température de 30° C (50° C - 20° C), la longueur de la tige du laiton, lorsqu'elle n'est pas contrainte, augmente par les cartes graphiques selon l'équation suivante :

δT = L(ΔT)= (0,3 m)(30° C)(1,88 x 10-5/° C) = 0,0001692 m

Nous notons que δD = 0,4 δC et que δ1 = δD + δB-D, où δB-D représente le changement de longueur de la tige de laiton.

δC = RAL / (AE)

Étant donné que pour la tige de l'acier, L = 0,9 m, A = πD2/4, D = 0,03 m et E = 105 x 109 Pa :

δC = 4 RA(0,9 m) / [π(0,03 m)2(105 x 109 Pa)] = 11,83797097 x 10-9 RA δD = 0,4 δC = 0,4 (11,83797097 x 10-9 RA) = 4,73518839 x 10-9 RA δB-D = RBL / (AE)

Étant donné que pour la tige du laiton, L = 0,3 m, A = πD2/4, D = 0,022 m et E = 105 x 109 Pa :

δB-D = 4 RB(0,9 m) / [π(0,03 m)2(105 x 109 Pa)] = 4,04203030 x 10-9 RB

Étant donné que RA = 0,4 RB :

δ1 = δD + δB-D = [4,73518839 x 10-9 (0.4 RB) + 4,04203030 x 10-9 RB] = 5,936105657 x 10-9 RB

Mais, δT = δ1 :

0,0001692 m = 5,936105657 x 10-9 RB RB = 28 503,536 N

Contrainte dans la tige de laiton

σB = RB/A = 4 (28 503,536 N) / [π (0,03 m)2] = 40 324 254 Pa

Par conséquent, σB = 40,324254 MPa

Comparaison des résultats

La contrainte dans la tige de laiton est essentiellement axiale. Toutefois, la représentation de la tige, ainsi que la façon dont elle est contrainte, permettent de produire des déflexions de flexion et des contraintes de pliage. Ce comportement n'est pas connu dans une vraie barre, qui est la base de la solution théorique. Pour éviter d'inclure les effets de flexion dans la comparaison, sélectionnez un point le long de l'axe neutre de la tige (où la contrainte de pliage est nulle). En outre, nous ne voulons pas vérifier les contraintes à proximité d'une contrainte ou d'une zone de contact, où les résultats peuvent être inclinés par les effets locaux. Par conséquent, nous comparons la contrainte axiale théorique du treillis (tige de laiton) au résultat de contrainte normale YY de Fusion au centre de gravité de la tige de laiton (-300, -150, 0). Le signe moins du résultat indique que la contrainte est comprimée, comme prévu (alors que les composants de contrainte positifs sont la traction) :

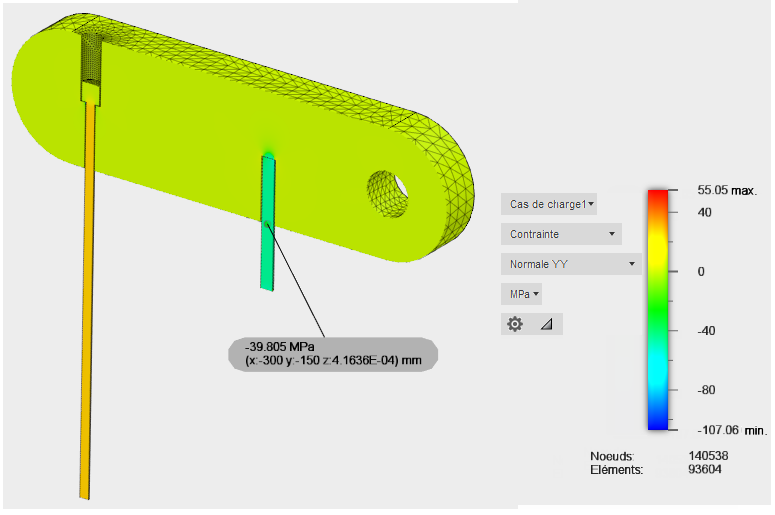
diagramme de contrainte thermique en Y

Emplacement	Résultat théorique (Beer et Johnston)	Fusion Résultat	% de différence
Centre de gravité de la tige de laiton	-40,324254 MPa	-39,805 MPa	-1.288 %

Remarque : vous pouvez attribuer la différence entre les résultats de l'étude de contrainte thermique et la solution théorique aux facteurs suivants :

Les extrémités de contact et les extrémités contraintes des tiges ne se comportent pas comme les extrémités des fermes réelles, qui se comportent comme des liaisons à billes. Des moments ou des réactions excentriques peuvent se produire aux extrémités des représentations de solides.
La zone de coupe des tiges solides est affectée par le maillage et ne correspond probablement pas exactement à la zone d'une coupe réellement circulaire.
La liaison quasi-rigide n'est pas vraiment rigide. La légère déformation du segment (due à la flexion sur sa longueur et à la compression locale au niveau des zones de contact de la tige) décharge partiellement les deux tiges. Cet effet réduit les magnitudes de contrainte calculées dans la tige de laiton.

Malgré ces différences connues entre les modèles d'éléments finis théoriques et solides, les résultats sont encore très proches.

Référence

Beer, Ferdinand P. and Johnston, Jr., E. Russell, Mechanics of Materials, McGraw-Hill, Inc., 1981, sample problem 2.4, page 58.