主応力の計算

応力は、全体座標系の X、Y、Z の方向とは異なる軸集合を基準として計算することができます。法線方向の応力だけが残るように座標系を回転すると、すべてのせん断応力はゼロになります。この方向では、サーフェスの法線ベクトルと、サーフェスに作用する応力ベクトルが、同一直線上にあります。この法線ベクトルの方向のことを、主応力方向と呼びます。面上の応力ベクトルの大きさは、主応力と呼ばれます。主応力には、第 1、第 2、第 3 の 3 つの値があります。多くの場合、これらの値はそれぞれ、最大主応力、中間主応力、最小主応力と呼ばれます。

主応力(σ1 および σ3)を求めるための計算式は、前に示した von Mises 応力の計算式よりも複雑です。まず、グローバル軸と主軸の間でラジアン単位の回転角度(φ)を決定する必要があります。

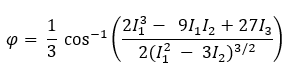
ここで、I1、I2、および I3 は、次の方程式によって決まる応力不変量です。

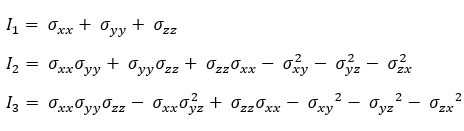
そして、第 1 主応力と第 3 主応力は次の方程式によって決まります。