準静的イベント シミュレーション スタディの理論

この理論的背景は、動的および準静的イベント シミュレーションの両方に当てはまります。

イベント シミュレーションでは、フックの法則(F=-kx)とニュートンの第 2 法則(F=ma)の原理を結合します。力の項を除去することによりこれら 2 つの方程式を結合すると、ma + kx = 0 となります。ここで減衰の影響(F=-cv)を追加すると、モーションに関する汎用の計算式が得られます。

ma+cv+kx = 0

ただし、m は質量、a は加速度、c は減衰の係数、v は速度、k は剛性、X は変位を示します。マトリックス形式で、この方程式は次のように表示されます。

[M]{a} + [C]{v}+[K]{x} = 0

この基本的な方程式から、変位ベクトル {x} および材料応答を制御している構成則を使用して、応力とひずみを決定することができます。

中央差分時間積分

イベント シミュレーションでは、中央差分時間積分アルゴリズムに組み込まれた明示的なソルバーを使用します。このアルゴリズムは、現在の状態(変位、速度、加速度)を直接解決するために、前の 2 つの状態に関する知識を使用します。ある状態から次の状態へのステップの大きさは、クーラント安定性の制限(安定したステップ増分)によって決定されます。この制限は、最大許容ステップを決定し、それを超えると解は失敗します。減衰の効果が考慮されると、これはこのように表されます。

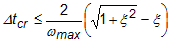
ここで、Δtcr は安定したステップ増分、ωmax はメッシュ内の最大の固有振動数、ξ は最も高いモードの臨界減衰比です。

一般的には、準静的イベント シミュレーションでの安定したステップ増分は非常に小さくなります。明示的なソルバーは、反復ごとに剛性マトリックスを形成する必要がないため、非常に効率的で比較的簡単に材料と接触の非線形性を処理することができます。節点の加速度を直接解析することができます。