유한 요소 분석을 통해 고유 진동수와 해당 모드 쉐이프를 결정하는 사용되는 기본 수학적 프로세스는 복잡합니다. 이 이론을 이해하기 쉽게 하기 위해 DOF(자유도)가 1인 매우 단순한 선형 스프링 질량 시스템을 고려해 보겠습니다. 즉, 질량은 단일 방향으로만 자유롭게 이동할 수 있습니다.

다음 이미지에서 m은 질량이고 k는 스프링의 강성입니다.

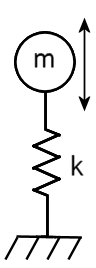
후크의 법칙은 강성의 스프링(k)을 거리(X)로 대치하는 데 필요한 힘(F)을 정의합니다.

(1) F = k·X

뉴턴의 운동 제2법칙은 단일 DOF 시스템에 대해 힘(F), 질량(m) 및 가속도(a) 간의 관계를 지정합니다.

(2) F = m·a

이러한 두 방정식을 결합하면 질량(m), 가속도(a), 스프링 강성(k) 및 변위(X) 간에 관계가 형성됩니다.

(3) m·a = k·X

다음 방정식은 이 단순한 선형 스프링 질량 시스템에 대한 진동의 각도 진동수(ω)(라디안/초)를 제공합니다.

(4) ω = (k/m)1/2

진동 주기당 2π 라디안이 있습니다. 따라서 다음 방정식은 진동의 고유 진동수(fn)를 헤르츠 단위로 제공합니다.

(5) fn = (k/m)1/2 / (2·π)

실제 유한 요소 모형에서는 메쉬의 모든 노드 및 요소 때문에 3D 동작과 많은 DOF가 있습니다.

주: 고유 진동수 계산에서는 댐핑을 고려하지 않습니다. 댐핑은 시스템에서 에너지를 방출시켜 나타나는 진동 진폭의 감소로 정의됩니다. 마찰, 점성 또는 기타 저항력을 극복하는 과정에서 에너지가 손실됩니다. 일반 제조 재질(예: 강철, 알루미늄 및 콘크리트)에서 발생하는 댐핑의 양은 작습니다. 따라서 댐핑이 없는 고유 진동수는 일반적으로 실제 고유 진동수에서 크게 다르지 않습니다. 댐핑은 댐핑 해제된 시스템을 기준으로 진동수를 줄입니다.

연속 시스템에는 무한한 수의 진동 모드가 있습니다. 그러나 유한 요소 모형에서는 DOF의 수가 유한하므로 진동 모드의 수도 유한합니다. 이러한 복잡한 3D 시스템의 진동 주파수와 모드 쉐이프를 결정하려면 매트릭스 연산, 고유 값 및 고유 벡터가 필요합니다.

방정식 (4)는 유한한 수의 솔루션을 사용하는 고유 값 및 고유 벡터 문제입니다. 각도 진동수(ω)는 스칼라 수량입니다. 특정 솔루션의 경우 모든 DOF는 동일한 각도 진동수에서 진동합니다. 그러나 진동의 진폭(δ)은 벡터 수량입니다. 이 복잡한 시스템에서 δ는 단일 DOF 예의 변위(X)와 유사합니다. DOF마다 δ의 구성요소에서 제공하는 다양한 진폭으로 진동합니다. 이 진폭 변형이 모드 쉐이프를 제공합니다.

고유 값 및 고유 벡터의 적절한 정의 및 모달 분석을 수행하는 데 사용되는 수학 연산은 이 항목에서 다루지 않습니다.