준 정적 이벤트 시뮬레이션 이론

이 이론적 배경은 동적 및 준 정적 이벤트 시뮬레이션 모두에 적용됩니다.

이벤트 시뮬레이션은 후크의 법칙(F=-kx)과 뉴턴의 제2법칙(F=ma)이 따르는 원칙을 결합합니다. 힘 항을 제거하여 이러한 두 방정식을 결합한 후에는 ma + kx = 0이 됩니다. 이제 댐핑 효과(F=-cv)를 추가하여 다음과 같은 일반적인 동작 방정식에 도달할 수 있습니다.

ma+cv+kx = 0

여기서 m은 질량, a는 가속도, c는 댐핑 계수, v는 속도, k는 강성, x는 변위입니다. 매트릭스 양식에서 이 방정식은 다음과 같이 표현됩니다.

[M]{a} + [C]{v}+[K]{x} = 0

이 기본 방정식에서 응력 및 변형은 변위 벡터{x}의 사용 및 재질 반응을 제어하는 구성 규칙에 따라 결정할 수 있습니다.

중심 차이 시간 통합

이벤트 시뮬레이션은 중심 차이 시간 통합 알고리즘을 기준으로 구축된 명시적인 솔버를 사용합니다. 이 알고리즘은 이전 두 상태에 대한 정보를 사용하여 현재 상태(변위, 속도 및 가속도)를 직접 해석합니다. 한 상태에서 다음 상태로 진행되는 단계의 크기는 허용되는 최대 단계를 제어하는 Courant 안정성 제한(안정 단계 증분)에 의해 구동되며, 이 제한을 초과하면 솔루션이 실패합니다. 댐핑 효과를 고려할 때 다음과 같이 표현됩니다.

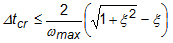
여기서 Δtcr은 안정 단계 증분이고, ωmax는 메쉬에서 가장 큰 고유 진동수이고, ξ는 가장 높은 모드에서의 임계 댐핑 분율입니다.

일반적으로 준 정적 이벤트 시뮬레이션에서 안정적인 단계 증분은 매우 작습니다. 명시적인 솔버는 매우 효율적이며 각 반복에서 강성 매트릭스를 형성할 필요가 없으므로 비교적 쉽게 재질과 접점 비선형성을 처리할 수 있습니다. 노드 가속도는 직접 해석할 수 있습니다.