Teoria dos materiais hiperelásticos

As características não lineares de tensão-deformação de materiais hiperelásticos, como a borracha, são complexas. Os muitos tipos de material disponíveis variam muito em comportamento. Para simulações não lineares em Fusion, os materiais hiperelásticos são representados usando o modelo de material padrão Mooney-Rivlin padrão de 2 constantes. Os coeficientes dos materiais são derivados por ajustes de curva obtidos experimentalmente pelos dados brutos de tensão-deformação. Estes dados podem ser baseados em vários ensaios, incluindo os seguintes exemplos de ensaios de tensão/compressão:

• Uniaxial (1 e 2)
• Plana
• Equi-biaxial
• Biaxial
• Confinado
• Triaxial
• Volumétrico

A descrição desses testes e dos dados brutos que eles produzem está além do escopo deste tópico. Os testes de materiais são realizados por laboratórios especializados no processo, e o ajuste de curva deve ser feito fora de Fusion. (O programa não tem um recurso incorporado para aceitar os dados brutos e executar a função de ajuste de curva). Existem vários programas disponíveis para executar a função de ajuste de curva necessária uma vez que os dados brutos são obtidos. Um desses programas é o HyperFit, que está disponível em uma versão demo freeware (funcionalidade limitada) e uma versão licenciada. Uma licença completa é necessária para gerar a curva e as constantes de material resultantes.

O modelo de material hiperelástico de Mooney-Rivlin

Os materiais hiperelásticos em Fusion são modelados usando o modelo de material padrão de 2 constantes de Mooney-Rivlin. A formulação quase incompressível é usada, de modo que termos volumétricos são incluídos na função de energia de deformação. Os efeitos da distorção de cisalhamento e da deformação volumétrica são separados.

Função energética geral da deformação de Mooney-Rivlin

A relação entre a energia de deformação, a distorção de cisalhamento e a deformação volumétrica é expressa na seguinte função de caso geral (aplicável aos casos de ordem superior e 2 constantes):

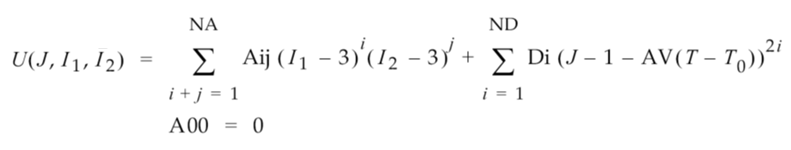
Em que:

• U é a energia de tensão.
• I1 é o primeiro invariante de deformação distorcional.
• I2 é o segundo invariante de deformação distorcional.
• J = det F, que é o determinado do gradiente de deformação.
• Aij é o conjunto de constantes de material relacionadas à distorção de cisalhamento (i e j sendo os subscritos das constantes individuais).
• Di é o conjunto de constantes de material relacionadas à deformação volumétrica.
• AV é o coeficiente volumétrico de expansão térmica.
• T é a temperatura atual
• T0 é a temperatura inicial

Equação simplificada de 2 constantes de Mooney-Rivlin

Atualmente, Fusion não suporta efeitos térmicos para materiais hiperelásticos em análises não lineares. Portanto, podemos simplificar a função anterior eliminando os termos de expansão térmica (AV, T e T0) e trabalhando a soma para as constantes Fusion aceita (A01, A10 e D1). A equação simplificada da energia de deformação passa a ser a seguinte:

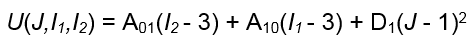
Em que:

• *U, J, I1* e I2 são os valores definidos anteriormente.
• A01 é a primeira de duas constantes de distorção relacionadas à deformação de cisalhamento do material.
• A10 é a segunda de duas constantes de distorção relacionadas à deformação de cisalhamento do material.
• D1 é a constante relacionada à deformação volumétrica do material, que é igual à metade do módulo de massa (K).

Ou seja, 2D1 = K. Portanto, D1 = K/2