Issue:
The documentation for "frictional stiffness for stick" (FSTIF) reads as follows (from the help for BSCONP):
The value of frictional stiffness should be chosen carefully. A method of choosing a value is to divide the expected frictional strength (MU * expected normal force) by reasonable value of the relative displacement before slip occurs. A large stiffness value may cause poor convergence, while too small a value may result in reduced accuracy. An alternative method is to specify the value of relative displacement using SMAX.
What does this mean?
Solution:
Frictional Stiffness for Stick (FSTIF)
In a theoretical world, the friction prevents any motion between the surfaces. That is not realistic in simulation, so springs are used to "prevent" motion; that is, the springs duplicate the "stick" that is caused by friction. The amount of motion while friction is restraining the parts is based on the "stiffness" of the springs:
In a theoretical world, the friction prevents any motion between the surfaces. That is not realistic in simulation, so springs are used to "prevent" motion; that is, the springs duplicate the "stick" that is caused by friction. The amount of motion while friction is restraining the parts is based on the "stiffness" of the springs:
F = k*x*n
where F is the horizontal force resisted by friction, k is the stiffness value (FSTIF), x is the relative displacement, and n is the number of active contact elements.
Note that the solver will calculate a default value for the frictional stiffness, so it is not necessary to provide a value. If you specify a value, one reason that the "stiffness should be chosen carefully" is because the parts do move when restrained by friction. If this motion is "large", it could affect other areas of the model. Check the displacement results to make sure any requirements for the analysis were not violated.
There are two conditions in which the friction springs are released, and the parts become free to move:
Note that the solver will calculate a default value for the frictional stiffness, so it is not necessary to provide a value. If you specify a value, one reason that the "stiffness should be chosen carefully" is because the parts do move when restrained by friction. If this motion is "large", it could affect other areas of the model. Check the displacement results to make sure any requirements for the analysis were not violated.
There are two conditions in which the friction springs are released, and the parts become free to move:
- The horizontal force (F) exceeds the friction force (normal force*friction coefficient).
- The horizontal displacement (x) is too large. This is controlled by the input "maximum allowable slip" (SMAX).
So FSTIF is a stiffness value used to restrict sliding when contact is in a stick condition. FSTIF along with SMAX affect how FSTIF works.
- If SMAX is left as the default value of 0.0, that means the frictional stiffness for stick is not updated. The default or user-entered value is used for all iterations during the solution.
- If SMAX is specified (a nonzero value), then FSTIF is used as an initial stiffness. If transverse displacement (x) exceeds SMAX, the stiffness is updated (increased) to reduce the displacement such that it is under SMAX.
To complicate things further, there is a parameter SLINESLIDETYPE that affects how contact stiffness is updated which affects friction stiffness as well.
Number of contact elements
The number of contact elements (n) created can be thought of as follows:
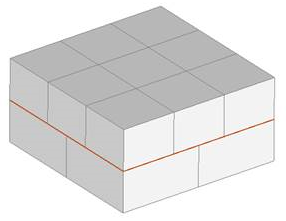
- Imagine one block on top, 3x3 mesh. This gives 9 faces, 16 nodes on the contact surface.
- Imagine a block on the bottom, 2x2 mesh. This gives 4 faces, 9 nodes on the contact surface.
- The number of contact elements created = number of nodes on secondary surface * number of faces on primary surface.
| Penetration Type | Primary | Secondary | Segments calculation | Segments |
| Unsymmetric | Bottom | Top | (4 faces x 16 nodes) | 64 |
| Unsymmetric | Top | Bottom | (9 faces x 9 nodes) | 81 |
| Symmetric | Both Top/Bottom | Both Top/Bottom | (4 faces x 9 nodes) + (9 faces x 9 nodes) | 145 |
The total number of contact elements created is given in the .OUT file:
NUMBER OF CONTACT SEGMENTS = 168
CONTACT SURFACE AREA = 4.0000E+00
During the solution process, the actual number of elements that are in contact ("active" using Nastran terminology) is given for each iteration in the .OUT file:
PERCENT OF TOTAL CONTACT ELEMENTS ACTIVE = 8.9
PERCENT OF ACTIVE CONTACT ELEMENTS CLOSED = 100.0
So in this example, (8.9/100)*168 segments = 15 contact elements are in contact (active) providing a force to prevent the parts from penetrating and from sliding.
See Also:
- Nastran documentation for BSCONP (includes FSTIF and SMAX)
- Nastran documentation for SLINESLIDETYPE