下列工作流介绍如何使用 AliasStudio 2009 中新增的“Align”工具。要使用该工具的早期版本(已重命名为 Align 2008),请参见 Align 2008 的工作流。
与其早期版本一样,“Align”工具可移动或者重塑曲线或曲面,以实现与其他曲线或曲面的位置连续性、切线连续性或 G2 曲率连续性。此外,还可实现 G3 曲率连续性。此工具还具有简化的界面、通过操纵器直接交互的功能以及更出色的输出。
如果启用了“Face selection”(在“Preferences”>“Selection Options”中),“Align”工具将允许通过单击线框内部来选择曲面。如果要选择曲面边,此工具会自动确定距鼠标位置最近的边。
对齐曲面边
- 选择“Object Edit”>“Align”>“Align”

 。
。 “Edge”是默认的“Alignment Type”。
- 单击要对齐的曲面边(输入曲面边)。
- 单击要与之对齐的曲面边(主曲面边)。该边也可以是等参线、面上线或修剪边。
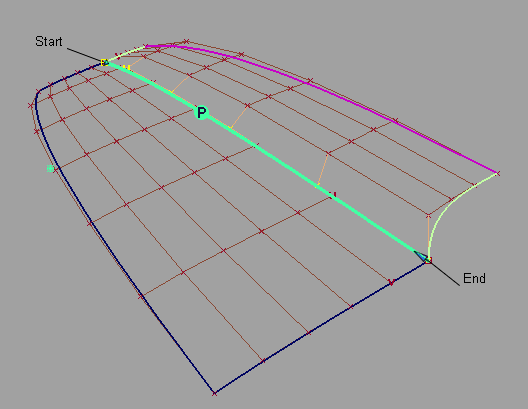
- 如有必要,使用“Position Influence”滑块对齐该边,以便实现位置连续性。
滑块值为 0.0 时,要对齐的曲面的参数化保持完整。当滑块移至 1.0 时,会尝试匹配主曲面的参数化,这样可实现更好的拟合。
- 如果需要,从选项窗口的“Continuity”下拉菜单中将连续性级别设置为“G1 Tangent”、“G2 Curvature”或“G3 Curvature”。
使用操纵器箭头可以直接操纵切线长度和曲率长度。
使用曲面外部的箭头可独立缩放每个边的切线长度或曲率长度。切线行或曲率行中间的箭头等量移动该行中的所有 CV。
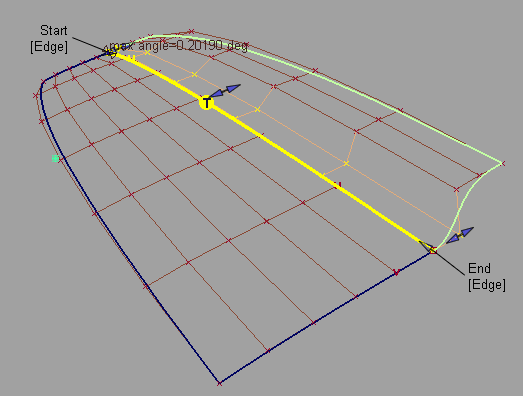
如果未达到所需的连续性,请尝试下列一种或多种操作:
- 调整“Position Influence”滑块。这将有助于沿边界排列 CV。
- 启用“Tangent Balance”,匹配主曲面的外壳线形状,或使用操纵器调整切线沿边的长度。
- 禁用“Explicit Control”。此时会自动将输入曲面的阶数设置为主曲面在对齐方向上的阶数。您还可以通过选项窗口手动调整阶数和跨距数。
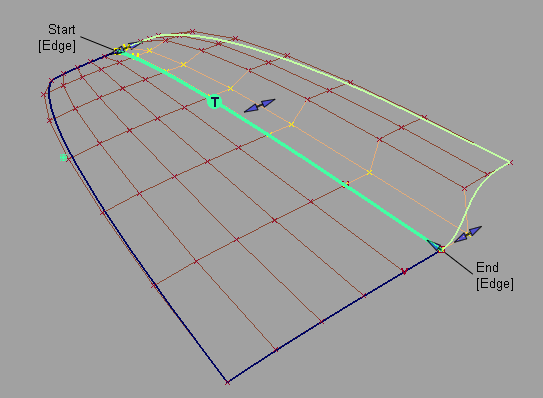
在此图中,“Position Influence”设置为 1.0,并且已禁用“Explicit Control”以匹配阶数。请注意,现在 CV 是如何沿边界完美排列的。
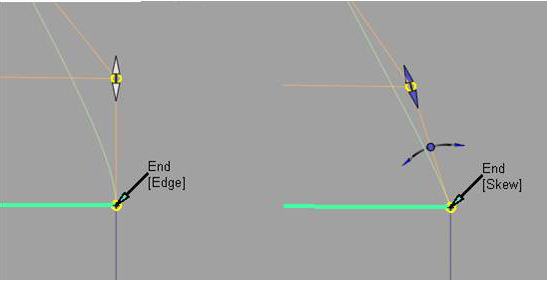
- 通过单击“Edge”标签在“Skew”或“Edge”对齐之间切换,更改外侧边对齐。或者设置“Start Align”和“End Align”(位于选项窗口的“Outer Edge”部分)。
选择“Skew”时,会显示一个可用于直接修改倾斜角度的旋转操纵器。也可以在选项窗口中指定一个具体的“Skew Angle”值。
如果选择了“Edge Align”,并且要与自然曲面边界对齐,您可以启用“Tangent Balance”以调整切线行上的 CV,从而使输入曲面的切线长度与主曲面的切线长度一致。如果“G2 Curvature”处于启用状态,这同样适用于曲率行 CV;如果“G3 Curvature”处于启用状态,则同样适用于下一行 CV。
这会将一个曲面与另一曲面边、修剪边、面上线或等参曲线对齐。
“Undo”(![]() +Z (Windows) 或
+Z (Windows) 或 ![]() +Z (Mac))操作适用于任何操纵器修改。
+Z (Mac))操作适用于任何操纵器修改。
将两个曲面部分对齐
- 选择“Object Edit”>“Align”>“Align”

 。
。 - 单击选项窗口中的“Partial”复选框以启用它。
- 单击要对齐的曲面边。
- 单击要与之对齐的曲面边(主曲面边)。
第一个曲面将和第二个曲面上与之最近的点对齐。
- 使用“Partial”操纵器修改端点的位置。
在捕捉到主曲面的一端时,“Partial”操纵器将从双侧箭头变为单侧箭头。
也可以使用选项窗口中的“Start”和“End”滑块。
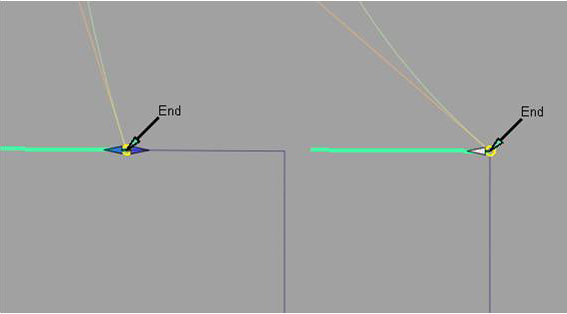
过渡对齐
- 在创建对齐后,单击选项窗口中的“Blending”复选框以启用过渡。
- 选择将应用过渡的“Extra CV Rows”数量。
- 修改“Blend factor”以便增加或减少原始对齐类型产生的影响。
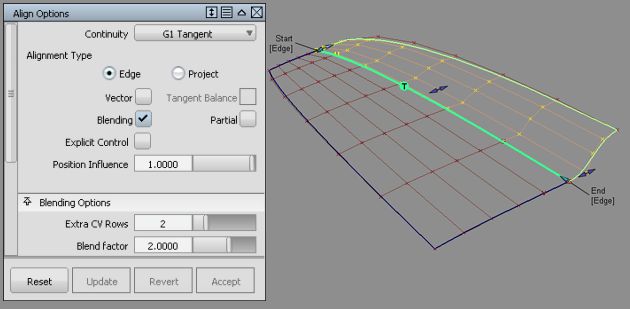
切线行上方的两行受过渡因子的影响。
过渡对齐会将过渡的影响延伸到曲面或曲线中。
还可以对位置对齐应用过渡,从而在对齐边上创建平滑的 CV 分布。
使用方向约束进行对齐(向量对齐)
- 建立边位置对齐。(请参见“对齐曲面边”中的步骤 1 到步骤 4)。
- 如果需要,使用“Explicit Control”滑块添加其他 CV。
- 将“Continuity”设置为“G1 Tangent”、“G2 Curvature”或“G3 Curvature”。
- 单击“Vector”复选框启用该选项。
选项窗口中会显示“Vector Options”部分。
- 执行以下操作之一:
- 选择“X”、“Y”或“Z”作为向量方向
- 选择“Picked”并选择现有向量
- 选择“View”,使用当前视图的方向作为向量方向。
- 选择“Normal”使用曲面法线作为向量方向。方向取决于曲面上 CV 的位置。
之后会沿向量修改切线和/或曲率 CV,以创建所需级别的相切或曲率。

如果使用选择的方向约束不能保持对齐,则所对齐曲面的边会显示为虚线。
建立位置对齐后,可以使用向量(方向)约束来对齐切线和曲率行。
可以通单击“Align”选项窗口底部的“Accept”按钮来应用顺序对齐,或单击“Restore”按钮来移除此类对齐。
通过将边投影到曲面上进行对齐(投影对齐)
- 选择“Object Edit”>“Align”>“Align”

 。
。 - 在选项窗口中将“Alignment Type”设置为“Project”。
- 选择要对齐的边。
此时显示“Vector Options”部分。
- 执行以下操作之一:
- 选择“X”、“Y”或“Z”作为向量方向
- 选择“Picked”并选择现有向量
- 选择“View”将当前视图的方向用作向量方向
- 选择“Normal”使用主曲面的法线(而不是使用单个向量)作为投影方向。
- 选择要与之对齐的曲面(主曲面)。
这条边会沿已定义的向量投影到主曲面上。此外,还会创建一条面上线,而且之后可以使用该曲线修剪主曲面。
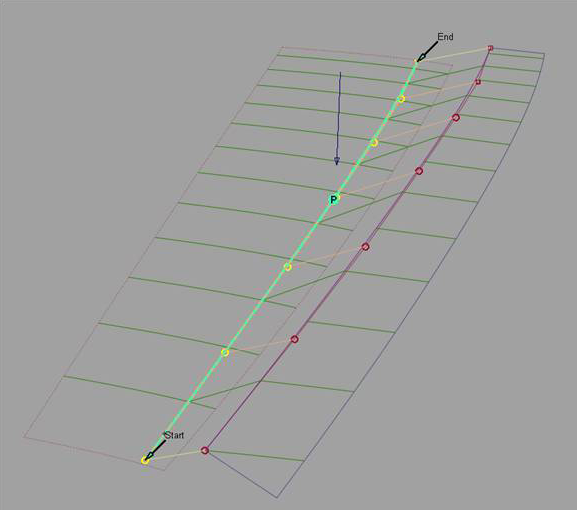 注:
注:如果要对齐的曲面边超出主曲面边界,则不能成功完成对齐。
注:如果不能使用选择的投影方向创建对齐,则所对齐曲面的边会显示为虚线。
提示:在对齐后,可以使用“Control Panel”>“Transform CV”修改 CV,以便对投影边进行修改。
可以沿向量将边投影到主曲面,从而将一个曲面与另一曲面的内侧对齐
将曲面边与一整条曲线对齐
- 选择“Object Edit”>“Align”>“Align”

 。
。 - 单击要对齐的曲面边。
- 单击曲线(主曲线)。
- 单击选项窗口中的“Partial”复选框以启用它。这样就可以只与主曲线的一部分对齐。
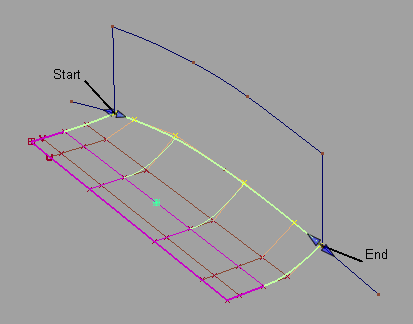
这会将曲面边的长度与曲线的长度对齐。
将曲线端点与曲面边、等参线或面上线对齐
- 选择“Object Edit”>“Align”>“Align”

 。
。 - 单击曲线(靠近要对齐的端点)。单击在要对齐到的点处的曲面边、等参曲线或面上线。
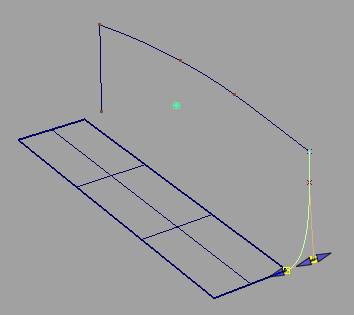
- 如果需要,将“Continuity”设置为“G1 Tangent”、“G2 Curvature”或“G3 Curvature”。
“Alignment Type”选项变为可用状态。“U/V”是默认值,可将自由曲线与选择为主曲线的曲面曲线方向对齐。
- 如果希望将曲线与曲面内部对齐,只需将“Alignment Type”设置为“Vector”即可,而无需使用面上线。
此时,切线对齐和曲率对齐由曲面在接触点的切线平面以及通过 Vector Options 指定的向量方向来定义。
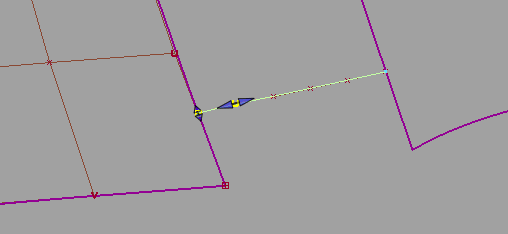
Alignment Type = Vector:此效果等同于在曲面上创建面上线,然后将自由曲线与之对齐。
这会将曲线端点与曲面曲线的端点对齐。
对齐两条曲线
- 选择“Object Edit”>“Align”>“Align”

 。
。 - 单击第一条曲线(靠近要对齐的端点)。
- 单击第二条曲线(靠近要对齐的端点)。
- 通过从选项窗口的“Continuity”下拉菜单中选择“G0 Position”、“G1 Tangent”、“G2 Curvature”或“G3 Curvature”来设置连续性级别。
操纵器箭头会变为可用,用于直接操纵连接点位置以及切线和曲率比例。
- 使用操纵器或控制窗口滑块修改“Attach Point”、“Tangent Scale”、“Curvature Scale”或“G3 Scale”的位置。

对齐具有位置连续性的曲线并修改“Attach Point”。
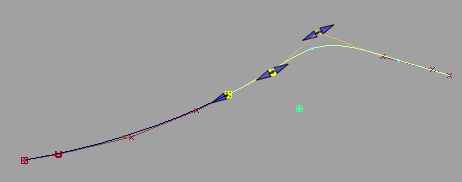
以 G2 曲率连续性对齐曲线。
对齐曲线或曲面的两端
- “Blending”等所有选项会参考两端的连续性设置。
- 在模型上单击显示在“Other Align”下的“[Activate]”标签,以在两个对齐操作之间切换。
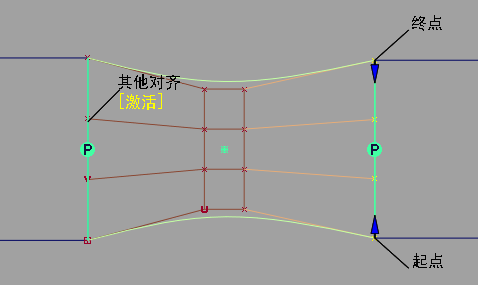
- “Object Edit”>“Query Edit”
 检索两端的构建历史,并且可以单击上方显示的“[Activate]”标签编辑两端的对齐。 注:
检索两端的构建历史,并且可以单击上方显示的“[Activate]”标签编辑两端的对齐。 注:当一条曲线或一个曲面与两条主曲线或两个主曲面对齐时,它有一个历史项,可以使用“Windows”>“Information”>“History View”查看。在这种情况下,初次单击“Revert”按钮将会还原到对齐方(上次对齐的一方)。此时历史将仅应用于另一方。再次单击“Revert”将删除该历史并将输入几何体还原到其原始形状。
在对齐曲线的两端或曲面的相对边时: