Analýzy

V prostředí součástí a konstrukcí používejte příkazy pro analýzu povrchu k analyzování součásti, abyste před zahájením výroby mohli ověřit geometrickou kvalitu. Můžete uložit několik různých analýz pro jeden specifický model nebo jeho různé druhy. Je například možné definovat různé způsoby analýzy pro určitou sadu součástí v jednom modelu.

Jakmile je použita analýza, vytvoří se v prohlížeči složka Analysis a do ní bude analýza umístěna. Každá uložená analýza se přidá do prohlížeče v pořadí, v jakém je vytvořena. V prohlížeči je zobrazen název a viditelnost aktivní analýzy spolu s názvem složky analýzy. Například Analýza: Zebra1 (zapnuto).

Můžete změnit viditelnost aktivní analýzy a vytvořit nové analýzy. Jakmile viditelnost u aktivní analýzy vypnete, zaškrtnutí políčka se potlačí a název vedle složky Analysis se změní na (Vypnuto). Grafika analýzy v grafickém okně se už přestane zobrazovat. Rozbalením složky Analysis zobrazíte všechny ostatní uložené analýzy a můžete provádět jejich správu. Aktivní analýzu můžete přepnout a libovolnou analýzu uloženou v seznamu můžete upravovat, kopírovat a vymazat.

Poznámka: Analýzy vytvořené v konstrukčním prostředí nelze ukládat a v prohlížeči modelu se neobjevují. Analýza z grafického okna zmizí, jakmile se uzavře dialog.

Poznámka: Stav viditelnosti analýzy se při uložení analýzy neukládá. Pokud uložíte součást s viditelnou analýzou, potom po dalším otevření součásti nebude analýza viditelná.

Zebra analýza

Analyzuje kontinuitu povrchu promítáním rovnoběžek na model. Výsledky ukazují, jak se světlo odráží od povrchu, abyste mohli zjistit oblasti, kde se musí kvalita povrchu zlepšit. Křivost je matematické naznačení vyhlazení mezi dvěma křivkami nebo povrchy. Míra změn směru se označuje jako křivost. Vyhlazení křivky je obvykle označováno pomocí písmena G a čísla.

Navázání G0 (bod) znamená, že se koncové body dotýkají. Přechod mezi dvěma hranami nebo povrchy je značný. Tento přechod může být ostrý nebo pozvolný. Následující obrázek ukazuje zebra analýzu průsečíku G0 mezi dvěma plochami. I když se plochy střetnou, pruhy se nesrovnají.

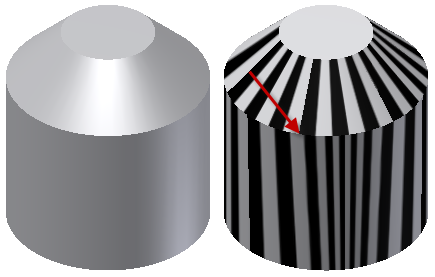
Kontinuita G1 (tečna) je hladký přechod mezi křivkami. Zdá se, že se tyto dvě křivky pohybují na spoji ve stejném směru, všimněte si ale míry změny (rychlosti) křivosti. Následující obrázek zobrazuje zebra analýzu průsečíku G1 mezi dvěma plochami. Mezi těmito dvěma plochami existuje tečné zaoblení. Hrany pruhu se sice srovnají, obsahují ale ostrý úhel.

Kontinuita G2 (křivost) je velice hladký přechod mezi křivkami. Tyto dvě křivky jsou shodné v koncových bodech, jsou tečné a mají ve spoji stejnou „rychlost“ (křivost). Následující obrázek zobrazuje zebra analýzu průsečíku G2 mezi dvěma plochami. Mezi těmito dvěma plochami existuje hladká (G2) zaoblení. Hrany pruhu jsou srovnány a mezi plochami mají vyhlazený přechod.

Analýza tahu

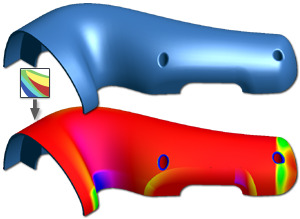
Posoudí, zda má model přiměřené zešikmení mezi součástí a formou (na základě směrového vektoru) a může se vyrábět odléváním. Spektrum ukazuje změny úhlu sešikmení v určitém rozsahu.

Hřebenová analýza zakřivení

Poskytuje vizuální analýzu zakřivení a celkové hladkosti ploch modelu, povrchů, křivek náčrtu a hran. Do konstrukčního prostředí je zahrnuta také analýza skupin a importovaných drátů. Diagram vektoru zakřivení uvádí zakřivení s řadou připojených trnů vycházejících z křivky. Relativní délka křivky se rovná zakřivení křivky v místě počátku osy. Delší trny označují oblasti s větším zakřivením a kratší trny označují menší zakřivení.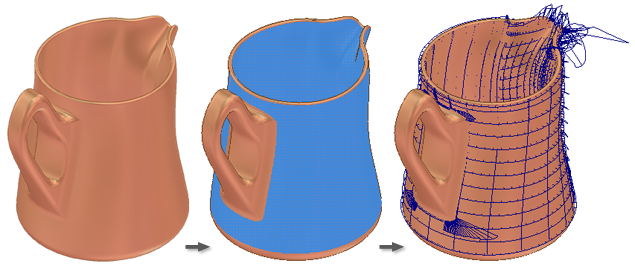

Výběrem jiné geometrie znovu použijete styl analýzy bez úpravy definice stylu.

Analýza Gaussova zakřivení

Analýza Gaussova zakřivení – posoudí oblasti velkého a malého zakřivení povrchu zobrazením barevného gradientu na povrchu součástí. Zobrazení gradientu je vizuální indikací povrchové křivosti, která používá výpočet analýzy Gaussovy křivosti , min. zakřivení nebo středního zakřivení.

MožnostGaussovazobrazí gradient, který představuje součin zakřivení; zakřivení ve směruu povrchu násobeno zakřivením ve směru v povrchu. Gaussova analýza je vhodná ke kontrole tvarů jako jsou spirály, prstence nebo tažení podél cesty spline.

Možnost Střední zakřivení: zobrazuje gradient představující střední zakřivení hodnot zakřivení povrchuu a v. Analýza středního zakřivení je vhodná ke kontrole tvarů jako je kužel nebo mnoha povrchů, které lze vytvořit pomocí funkce šablonování.

Možnost Max. zakřivení: zobrazuje gradient představující ty vyšší zu a v hodnot zakřivení povrchu. Analýza maximální křivosti je vhodná pro ty případy, kdy chcete v součásti nebo na povrchu nalézt oblasti s vysokým či nízkým zakřivením.

Výpočet zakřivení

V libovolném bodě křivky v rovině je tečna čarou, která nejlépe aproximuje křivku procházející tímto bodem. Jinak můžete také najít nejlepší aproximační kružnici, která prochází tímto bodem a dotýká se této křivky. Převrácenou hodnotou poloměru této kružnice je zakřivení křivky v tomto bodě.

Nejlepší aproximační kružnice může ležet vlevo nebo vpravo od křivky. Pokud je to základ, zavede se potom nějaká konvence, například že křivost bude mít kladné znaménko, pokud kružnice leží vlevo a záporné znaménko, pokud kružnice leží vedle křivky vpravo. To je známo jako křivost se znaménkem.

Křivost kolmého řezu je zobecnění křivosti vůči povrchům. Když je dán bod na povrchu a směr ležící v tečné rovině povrchu v tomto bodě, křivost kolmého řezu se vypočte průsečíkem:

povrchu s rovinou překlenutou tímto bodem,
kolmicí k povrchu v tomto bodě,
se směrem.

Křivost kolmého řezu je křivost se znaménkem této křivky v zájmovém bodě.

Hlavní zakřivení plochy v bodě jsou minimální a maximální normálová zakřivení daného bodu. (Normálová zakřivení jsou zakřivení křivek na ploše, která leží v rovinách, včetně tečného vektoru v daném bodě.) Hlavní zakřivení se používají k výpočtu Gaussova a středního zakřivení plochy.

Gaussovo zakřivení plochy v bodě je výsledkem hlavní křivosti v daném bodě. Tečná rovina každého bodu s pozitivním Gaussovým zakřivením se dotýká plochy v jednom bodě, zatímco tečná rovina každého bodu s negativním Gaussovým zakřivením plochu protíná. Každý bod s nulovým středním zakřivením má negativní nebo nulové Gaussovo zakřivení.

Analýza řezu

Poskytuje základní (zjednodušené) nebo podrobné (rozšířené) informace a odpovídající grafiku více řezů vnitřku těles. Také analyzuje, jestli součásti splňují minimální a maximální tloušťku stěn. Není dostupná v konstrukčním prostředí. V grafickém okně se zobrazí odpovídající sady obrazů průřezu.

Poznámka: Rovina řezu, která těleso neprotíná, má oblast 0.0 a nemá příslušný obraz v grafické oblasti.

Typ Zjednodušené analýzy vygeneruje pohled řezu součástí v jedné rovině řezu. Typ Rozšířené analýzy poskytne tabulku detailnějších informací o vícenásobných oblastech řezu modelem společně s příslušným obrazem průřezu.

Poznámka: Můžete upravovat typ uložené analýzy a potom přepínat z jednoho typu na druhý. Přepínání typů však může vést ke ztrátě dat základního nastavení. Pokud si například nastavíte řadu řezů pro rozšířenou analýzu, potom změníte typ na Zjednodušenou, opět upravujete analýzu a znovu přepnete na Rozšířenou, potom se nastavení řezu z prvního Rozšířeného nastavení ztratí.

Poznámka: Jakmile dojde v budoucím výpočtu k přemístění referenční roviny nebo rovin řezu, analýza se ihned aktualizuje, pokud bude viditelná. Pokud není viditelná, dojde k aktualizaci, až bude analýza příště viditelná a aktivní.

Rozdíly mezi analytickými příkazy v prostředí součásti a v prostředí konstrukce

V prostředí součásti můžete uložit každou analýzu a potom je spravovat pomocí prohlížeče modelu. Mezi položkami, které si můžete vybrat, jsou plochy, pokrývky nebo celé pevné těleso součásti.

Analýzy, které vytvoříte v prostředí konstrukce, jsou jenom dočasné a můžete je odstranit až po uzavření dialogu. Kromě výběru ploch a pokrývek můžete vybrat také skupiny. Pro analýzy vektorů zakřivení můžete vybrat také Dráty. Průřezová analýza není v prostředí konstrukce dostupná.