Die Berechnung dieser Spannungen umfasst mehrere Schritte. Es wird mit der Integration der sechs Spannungen σ N σ T σ H τ NT τ TH τ NH entlang der SLK begonnen, um die Gesamtlast zu erhalten (F N , T , F H , F NT , F TH , F HN ), indem Folgendes verwendet wird:
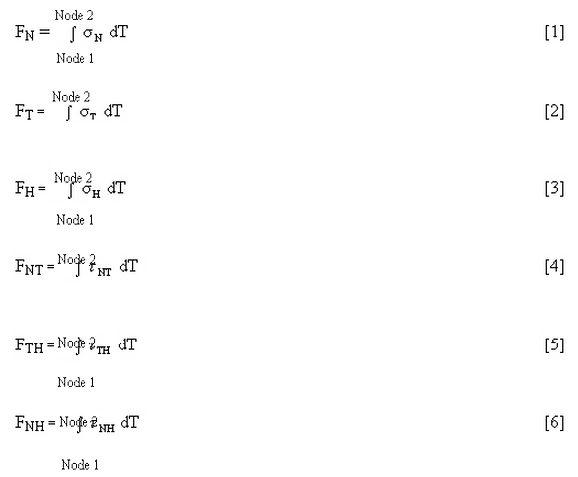
T ist die Position entlang der SKL.
Anschließend wird die Membranspannung (F/A) für alle 6 Komponenten berechnet. Für eine SKL der Länge t:
Die wichtigsten Membranspannungen (
) werden aus dem Tensor abgeleitet, dessen Komponenten durch die Gleichungen 7 bis 12 gegeben sind. Diese Spannungen werden ermittelt, indem dieser Tensor in der Hauptachse umgeformt wird.
Im nächsten Schritt werden die Biegespannungen durch Subtrahieren der Membranspannung von der gesamten Lastverteilung ermittelt. Dies erfolgt von Spannungspunkt zu Spannungspunkt. Es müssen nur die beiden Komponentenspannungen lotrecht zur SKL berücksichtigt werden (nominell die Ring- und meridionalen Komponentenspannungen). Im ersten Schritt wird die Verteilung der Momentlast für die SKL der Länge t ermittelt. Dann wird die Verteilung der Momentlast integriert, um das Moment auf dem Querschnitt zu bestimmen.
Diese Integrale sollten erneut mit der Trapezintegration berechnet werden. Die nachfolgenden Ergebnisse werden zur Berechnung der Biegespannung (Mc/I) für die SKL der Länge t mit folgenden Formeln verwendet:
Im nächsten Schritt wird die Hauptspannung an jedem Ende der SKL (
) berechnet. Die wichtigsten Membran- und Biegespannungen werden aus dem Tensor abgeleitet, dessen Komponenten durch Ersetzen von T = Knoten 1 und T = Knoten 2 abgeleitet werden.
Die Membranspannungen werden durch die Gleichungen 7 bis 12 und die Biegespannung durch die Gleichungen 16 bis 18 ermittelt. Achten Sie darauf, wie zwei Sätze von Hauptspannungen abgerufen werden: einer bei T = Knoten 1 und ein anderer bei T = Knoten 2. Die Hauptspannungen werden ermittelt, indem der Tensor wieder in der Hauptachse umgeformt wird.
An diesem Punkt sind alle Hauptspannungen
und
,
vorhanden, die zum Bestimmen der beiden ausgegebenen Skalare erforderlich sind: P m und P m + P b :
|
P m = Größter Wert von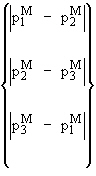 
|
(25) |
|
Pm + Pb = Größter Wert von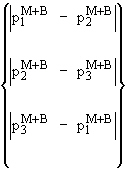 
|
(26) |
Beachten Sie, dass die Gleichung 26 zweimal ausgewertet werden muss, da zwei Gruppen von Werten vorhanden sind: eine bei T = Knoten 1 und eine andere bei T = Knoten 2. Die Ausgangsgröße sollte der Größe der Auswertung entsprechen, die den größten Wert ergab.
Literatur: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev. 4, 2000.