For transient analyses, the transient terms are discretized using an implicit or backward difference method. Using the matrix algebra notation, a typical steady-state transport equation (momentum, energy, turbulence variables, scalar) can be written:
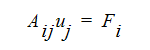
where Aij contains the discretized advection and diffusion terms from the governing equations, uj is the solution vector or values of the dependent variable (u, v, w, T, K,....) and Ficontains the source terms.
The transient terms in the governing equations took the form:
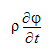
where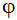 
represents the dependent variable (u, v, w,....). This term is discretized using a backward difference:
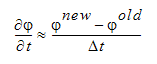
We can add this term to the matrix equation above:
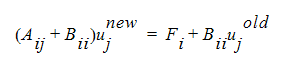
where Bii is a diagonal matrix composed of terms like:
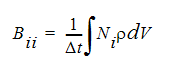
This discretized transient equations must be solved iteratively at each time step to determine all of the new variables (variable values at the latest time).