In Autodesk Simulation CFD, the finite element method is used to reduce the governing partial differential equations (pdes) to a set of algebraic equations. In this method, the dependent variables are represented by polynomial shape functions over a small area or volume (element). These representations are substituted into the governing pdes and then the weighted integral of these equations over the element is taken where the weight function is chosen to be the same as the shape function. The result is a set of algebraic equations for the dependent variable at discrete points or nodes on every element.
Streamline Upwind Advection Schemes
With the exception of the continuity equation, the governing equations describe the transport of some quantity (e.g., U, V, T) through the solution domain. The governing equations take the form:
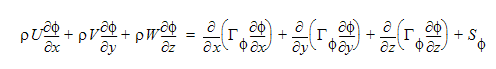
Note that the general scalar transport equation is also in a similar form without a source term.
The finite element method described above is used directly on the diffusion and source terms. However for numerical stability, the advection terms are treated with upwind methods along with the weighted integral method. Four of the upwind methods used in Autodesk Simulation CFD are described below:
ADV 1:Monotone streamline upwind
- numerically stable
- 1 < order < 2
- recommended for meshes aligned with flow direction
- numerically diffusive for meshes not aligned with flow
- works well for geometries with lots of internal obstructions
- works well for extruded meshes
ADV 2: Petrov-Galerkin
- moderate numerical stability (less than ADV 1)
- 2 < order < 3
- less numerical diffusion for random meshes
- recommended for pressure driven flows
- recommended for compressible flows
- default for scalar and energy transport equations
ADV 3: Flux-based scheme
- numerically unstable for most flows
- order > 3
- uses multiple elements upstream to form advection terms
- can ONLY be used for INCOMPRESSIBLE flows
- CANNOT be used for moving solids analyses
- specially tuned for drag or external flow problems
ADV 4: Min-Mod scheme
- Petrov-Galerkin variant
- 2 < order < 3
- moderate numerical stability (less than ADV 1)
- specially tuned for flows in long narrow ducts
As an example of the upwind treatment for the advection terms, let’s look at the monotone streamline (ADV 1). For this upwind method, the advection terms are transformed to stream-wise coordinates:

where s is the streamwise coordinate and Us is the velocity component in the stream-wise coordinate direction. For a pure advection problem this term is a constant. With this in mind, the weighted integral of the advection terms can be written as:
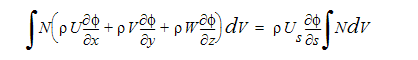
In the other advection schemes, the shape function is modified to account for streamline curvature in the element.