Simulate the mixing of two similar fluids by using a Scalar boundary condition and by defining scalar-dependent fluid properties.
Scalar Boundary and Property Variation
To simulate the mixing of two fluids, use the Scalar boundary to track the relative concentrations of the two fluids. For example, assign a Scalar boundary condition of 0 to represent the first fluid, and a Scalar boundary condition of 1 to represent the other. This is in addition to the typical velocity or flow rate boundary conditions needed to drive the flow
A single material is defined within the flow region, and is defined so that its properties depend on the scalar condition. For example, a piece-wise linear variation for density as a function of scalar will cause the density to vary based on the relative concentration of the two fluids. The other properties, viscosity, conductivity, etc., can be varied in the same way.
Diffusion Coefficient
To properly simulate the mixing, a diffusion coefficient is a required input. On the Solve dialog, enable the General Scalar from the Advanced dialog, and input a value of diffusion coefficient.
The diffusion coefficient controls the mass diffusivity of the scalar quantity into the surrounding fluid. A value of 0 will prevent any diffusion of the scalar quantity. This quantity is DAB in Fick’s Law:
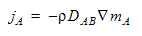
where jA is the mass flux of species A. This is how much of A is transferred (per time and per unit area normal to the transfer direction). It is proportional to the mixture mass density, and to the gradient of the species mass fraction, mA. The units of the Diffusivity coefficient are length squared per time.
Some sample values of diffusion coefficients are given:
|
Fluid 1 |
Fluid 2 | Diffusion Coefficient |
| Air (STP) | Propane | 0.1 cm²/s |
| Air (STP) | LNG | 0.16 cm²/s |
| Air (STP) | Gasoline | 0.05 cm²/s |
| Air (STP) | Hydrogen | 0.61 cm²/s |
| Air (STP) | Carbon Dioxide | 0.16 cm²/s |
| Air (STP) | Oxygen | 0.20 cm²/s |
| Air (STP) | Water Vapor | 0.25 cm²/s |
The diffusion coefficient of a fluid is typically 10,000x greater in air than in water.
Example: Mixing Air and CO2
To mix air and carbon dioxide in a vessel, we first decide (arbitrarily) that air will be represented by a scalar value of 0, and carbon dioxide with a scalar value of 1.
The two streams will come in through separate inlets, mix, and then exit through the outlet.
The boundary conditions for the air inlet are the velocity (or flow rate) and a scalar condition = 0. The boundary conditions for the carbon dioxide inlet are the velocity (or flow rate) and a scalar condition = 1:

Assign a single material to the vessel, but modify the density as a function of scalar. The piecewise linear variation method is the most convenient variation method. The density of air is 1.2047 e-6 g/mm3, and the density of carbon dioxide is 1.773e-6 g/mm3. The table would look like this:

The other properties can be varied in the same manner. Density will typically have the greatest influence on the solution, but viscosity can be varied as well.
Before applying the material, click Edit on the Environment dialog, and select Variable. This is needed to allow the material properties to vary.
On the Physics tab of the Solve dialog, click the Advanced button, and enable General Scalar. Because we are mixing air and carbon dioxide, we need to specify a diffusivity coefficient of 16 mm2/s.
When the analysis is run, the scalar quantity will propagate throughout the vessel based on the flow, and the material will adjust in response to the scalar. The Flow and Scalar solutions should be run together because the properties vary with the flow solution.
Related Topics
Applying Scalar Boundary Conditions