Composite materials properties are used only for the thin and thick composite elements. To properly enter the properties, the material axes must be defined in the Element Definition dialog box. (See the pages Thick Composite Elements and Thin Composite Elements.)
The composite material properties are listed below. Depending on the element type, analysis type and loads, not all the material properties may be required. In addition to these properties, it may be necessary to define some Isotropic Material Properties.
Symbols used throughout this section are defined as follows:
E f modulus of elasticity of the fiber material
E m modulus of elasticity of the matrix material
G f shear modulus of elasticity of the fiber material
G m shear modulus of elasticity of the matrix material
μ f Poisson's ratio of the fiber material
μ m Poisson's ratio of the matrix material
V f fraction of total volume taken up by the fiber material
V m fraction of total volume taken up by the matrix material (=1-V f )
Elastic Properties
- Modulus of Elasticity Local Axis 1 (E1): The modulus of elasticity for local axis 1 is the slope of the stress versus strain curve of local axis 1 of a material until the proportionality limit. This is also referred to as the Young's modulus of local axis 1. Also, for a fibrous composite material the following equation may be used: E1 = V f *E f + V m *E m where the properties are in the direction of local axis 1. This property is applicable to both types of composite elements and is required for all structural analysis types.
- Modulus of Elasticity Local Axis 2 (E2): The modulus of elasticity for local axis 2 is the slope of the stress versus strain curve of local axis 2 of a material until the proportionality limit. This is also referred to as the Young's modulus of local axis 2. Also, for a fibrous composite material the following equation may be used: E2 = V f *E f + V m *E m where the properties are in the direction of local axis 2. This property is applicable to both types of composite elements and is required for all structural analysis types.
- Poisson's Ratio Local Plane 12 (Major) (μ 12 ): The Poisson's ratio for local plane 12 is found by taking the negative lateral strain in the local plane 12 and dividing it by the axial strain in the direction normal to the local plane 12 for an axially loaded member. (μ 12 = -strain direction 2/strain in direction 1) Typical values for Poisson's ratio range from 0.0 to 0.5. For a fibrous composite the following equation can be used: μ 12 = V f *μ f + Vm* μ m where the properties are measured in the 12 plane. Poisson's ratio for local plane 12 can be referred to as the major Poisson's ratio. This property is applicable to both types of composite elements and is required for all structural analysis types.
- Poisson's Ratio of Local Plane 21 (Minor) ( μ 21 ): For a fibrous composite (orthotropic material) the following equation can be used:μ 21 =μ 12 *(E2/E1). Poisson's ratio for local plane 21 can be referred to as the minor Poisson's ratio. This property is applicable to both types of composite elements and is required for all structural analysis types.
- Thermal Coefficient of Expansion for Local Axis 1: The thermal coefficient of expansion for local axis 1 is a property based on the contraction and expansion of the material. This property is applicable to both types of composite elements and is required for all structural analyses that involve thermal loads.
- Thermal Coefficient of Expansion for Local Axis 2: The thermal coefficient of expansion for local axis 2 is a property based on the contraction and expansion of the material. This property is applicable to both types of composite elements and is required for all structural analyses that involve thermal loads.
- Shear Modulus of Elasticity of Local Plane 12 (G12): The shear modulus of elasticity of local plane 12 (in the plane of the element) is the slope of the shear stress versus shear strain of plane 12 of a material until the proportionality limit. This is also referred to as the modulus of rigidity. For a fibrous composite the following equation can be used: G 12 = (G f *G m )/(V m *G f + G m V f ). This property is applicable to both types of composite elements and is required for all structural analysis types.
- Shear Modulus of Elasticity of Local Plane 13: The shear modulus of elasticity of local plane 13 (perpendicular to the element) is the slope of the shear stress versus shear strain of plane 13 of a material until the proportionality limit. This is also referred to as the modulus of rigidity. This property is only applicable to thick composite elements and is required for all structural analysis types.
- Shear Modulus of Elasticity of Local Plane 23: The shear modulus of elasticity of local plane 23 (perpendicular to the element) is the slope of the shear stress versus shear strain of plane 23 of a material until the proportionality limit. This is also referred to as the modulus of rigidity. This property is only applicable to thick composite elements and is required for all structural analysis types.
Allowable Stresses
The allowable stresses are required if a Tsai-Wu or Maximum Stress failure criteria is specified. Refer to the pages Thick Composite Elements and Thin Composite Elements for the selection of the failure criteria and the equations that govern failure.
- Compressive Stress of Local Axis 1 (X c ): The allowable compressive stress of local axis 1 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements. A positive value needs to be entered.
- Tensile Stress of Local Axis 1 (X t ): The allowable tensile stress of local axis 1 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
- Compressive Stress of Local Axis 2 (Y c ): The allowable compressive stress of local axis 2 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements. Enter a positive value.
- Tensile Stress of Local Axis 2 (Y t ): The allowable tensile stress of local axis 2 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
- Shear Stress of Local Plane 1-2 Plane S: The allowable shear stress of the local 12 plane is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
- Stress interaction F12 (Tsai-Wu): The stress interaction F12 is a failure criteria property that is used only for the Tsai-Wu failure theory. It is determined from biaxial tests. For numerical stability, the following condition must be satisfied:
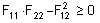 .
. - Core Crushing (Zc): When a thin plate is bent, one surface is in tension and the other is in compression. The vertical components of those two stresses (top and bottom) cause the crushing of the core layer (lamina). The core crushing allowable is the allowable stress that can occur before the core material crushes. It applies only to the maximum stress failure theory and only for thick composite elements. Enter a positive value.
- Allowable transverse shear stress in 13 plane (S 13 ): The allowable transverse shear stress in the local 13 plane (perpendicular to the element) is a material property that is used in different failure criteria for a composite element analysis. It applies only to the maximum stress failure theory and only for thick composite elements.
- Allowable transverse shear stress in 23 plane (S 23 ): The allowable transverse shear stress in the local 23 plane (perpendicular to element) is a material property that is used in different failure criteria for a composite element analysis. It applies only to the maximum stress failure theory and only for thick composite elements.
Allowable Strains
The allowable strains are required if the maximum strain failure criteria is specified. Refer to the pages Thick Composite Elements and Thin Composite Elements for the selection of the failure criteria and the equations that govern failure.
- Compressive Strain of Local Axis 1(T 1c ): The allowable compressive strain of local axis 1 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements. Enter a positive value.
- Tensile Strain of Local Axis 1 (T 1t ): The allowable tensile strain of local axis 1 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
- Compressive Strain of Local Axis 2 (T 2c ): The allowable compressive strain of local axis 2 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements. Enter a positive value.
- Tensile Strain of Local Axis 2 (T 2t ):The allowable tensile strain of local axis 2 is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
- Shear Strain of Local Plane 1-2 Plane S: The allowable shear strain of the local 12 plane is a material property that is used in different failure criteria for a composite element analysis. This property is applicable to both types of composite elements.
Flexure Controls
By default, the flexural properties is calculated from the elastic properties. To use specific values for the flexural properties, activate the Flexural Modulus check box, and then enter the following properties.
- Flexural Modulus of Local Axis 1: The flexural modulus of local axis 1 is the slope of the moment-curvature curve in the local 1 direction before the proportionality limit. This property is applicable to both types of composite elements.
- Flexural Modulus of Local Axis 2: The flexural modulus of local axis 2 is the slope of the moment-curvature curve in the local 2 direction before the proportionality limit. This property is applicable to both types of composite elements.
- Flexural Poisson's Ratio of Local Plane 12: The flexural Poisson's ratio is the ratio of the curvature in the local 1 direction to the curvature in the local 2 direction. This property is applicable to both types of composite elements.
- Torsional Rigidity of Local Plane 12: The torsional rigidity of the local plane 12 is comparable to the shear modulus. If no value is provided, a value is calculated using the flexural modulus and the flexural Poisson's ratio. This property is applicable to both types of composite elements.