Selección de una curva

Cuando se utiliza el gráfico de entrada de datos para definir valores que puedan variar con la simulación , se ofrecen varias opciones para definir los sectores de la curva . Estas opciones están en forma de leyes o funciones matemáticas que crean tipos de curvas específicos.

Nota: Si los datos de salida se consumen en una fórmula definida por el usuario, su nombre en el navegador se agrega al nombre original de la salida entre paréntesis. Por ejemplo: “Fuerza (Revolución:7)”

Selección de funciones matemáticas y definición de sus parámetros

Para definir cada sector de una curva, se asignan funciones matemáticas, es decir, leyes. Se pueden crear varios sectores sucesivos de forma que cada uno tenga su propia ley o una suma de distintas leyes (por ejemplo, una función de seno más una función de tramo). Por ejemplo, puede crear un primer sector con un tramo cúbico y un segundo sector con un seno. El software impone el principio de continuidad de las leyes globales. Este comportamiento puede confundir el primer punto del segundo sector y el último punto del primer sector, y provocar el desplazamiento automático de otros puntos. Con frecuencia, para obtener la curva deseada inicialmente, se deben añadir funciones adicionales.

Después de seleccionar una ley y desplazarla a la lista del cuadro de leyes del sector, es necesario añadir parámetros para la ley. Para añadir parámetros debe hacer lo siguiente:

Una vez se ha seleccionado un sector de curva y se han añadido las condiciones que se desean aplicar, se puede definir el sector de curva seleccionado.

En el cuadro Lista de leyes disponibles, pulse la flecha abajo para seleccionar la ley que desea utilizar.
Pulse para reemplazar la ley actual del sector con la ley seleccionada en la lista de sectores.
Se pueden seleccionar y reemplazar leyes tan a menudo como sea necesario, pero la nueva ley sobrescribe la ley mostrada en la lista del cuadro de leyes del sector.

Se pueden sumar múltiples leyes en el mismo sector. Si desea añadir leyes adicionales para un sector, repita el primer paso y este paso, pero pulsando . Para eliminar una ley en un sector que contiene múltiples leyes, seleccione la ley que desea eliminar en la lista del cuadro de leyes del sector y pulse .

En la lista del cuadro de leyes del sector, introduzca las propiedades necesarias para la ley mostrada.

Si muestra

Introduzca las propiedades de

Tramo lineal, Tramo cúbico, Cicloide, Armónico, Seno modificado, Trapezoide modificado

Las coordenadas (X1, Y1) y (X2, Y2) de los puntos que definen la curva o introduzca un valor para Inclinación para definir el degradado medio de la línea. La curva puede definirse introduciendo las coordenadas de los puntos inicial y final o introduciendo las coordenadas del punto inicial y el gradiente medio del sector.

La curva es simétrica en torno a la mitad del sector.

El área situada bajo la curva es igual a la del triángulo bajo un tramo lineal equivalente.

Tramo lineal tiene una inclinación constante, es decir, los dos puntos del sector están vinculados mediante una línea recta.

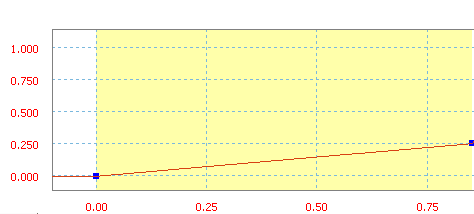
Tramo lineal con una inclinación de 30 pul/s.

Tramo cúbico está definido mediante un polinomial de tercer orden.

Tramo cúbico con una inclinación media de 70 pul/s.

Cicloide es una función de tramo desde seno/coseno.

Tramo cicloide con una inclinación media de -50 pul/s.

Armónico es una función de tramo desde seno/coseno.

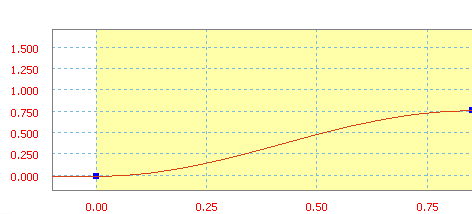
Tramo harmónico con una inclinación media de 90 pul/s.

Seno modificado es una función de tramo desde seno/coseno.

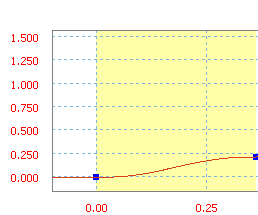
Tramo de seno modificado con una inclinación media de 60 pul/s.

Trapezoide modificado es una función de tramo desde seno/coseno.

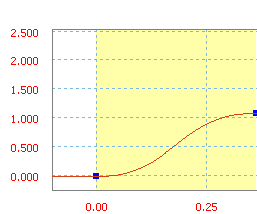
Tramo de trapezoide modificado con una inclinación media de 300 pul/s.

Si muestra	introduzca
Seno	Valor de Amplitud que indica la altura de la curva desde la media del ciclo para que Frecuencia muestre el número de ciclos por unidad de eje X, y para que Fase muestre las distancia desde el inicio de un ciclo hasta el comienzo del sector. Seno es una función clásica. Las unidades de amplitud son las mismas que para la variable controlada (movimiento impuesto, fuerza). Las unidades de frecuencia son la inversa de la variable utilizada en el eje X (en Hz si es tiempo). La fase se expresa en grados o radianes.
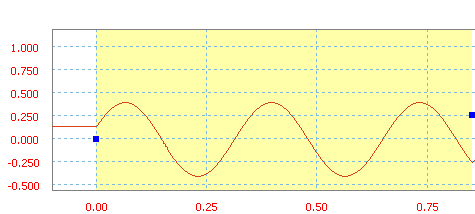
Seno con una amplitud de 40, una frecuencia de 3 Hz y una fase de 20 grados.
Polinomial	Polinomial es una función polinomial y, en este caso, tiene hasta cinco grados. Existen dos métodos para definir los coeficientes del polinomio. Método 1: especificación de los valores de los coeficientes Introduzca un valor para a0 y tantos de los siguientes valores de a como desee. Método 2: importación de un archivo de texto abre el cuadro de diálogo Abrir, lo que permite importar un archivo que define el polinomial. Orden define el orden del polinomial para la curva en el sector seleccionado. calcula el valor constante y los valores a las primeras cinco órdenes del polinomial. a0, a1, a2, a3, a4, a5 muestra el valor constante y los valores a las primeras cinco órdenes del polinomial. Los valores pueden editarse. El archivo de texto debe tener el siguiente formato: //comentarios: las líneas de comentarios son opcionales y vienen precedidas por dos barras inclinadas. x1 y1: lista de puntos basada en los valores de x e y. ...: una definición de punto por fila o por línea. xn yn: tantos puntos como sean necesarios. Puede introducir los valores deseados o el software puede calcular los términos automáticamente utilizando el método de interpolación menos cuadrado.
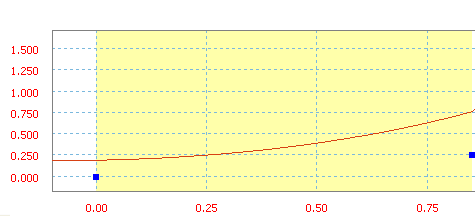
Polinomial con a0=20 pulg, a1=10 pulg/s, a2=50 pulg/s² y a3=20 pulg/s³.
Spline	Valor de Inclinación para definir la inclinación de la línea. Spline es una función cúbica utilizada para interpolar entre puntos sucesivos. Una spline se puede definir de varias formas. Son las siguientes: Puede definir rápidamente los puntos de entrada con el ratón en la región gráfica pulsando dos veces o con el botón derecho y seleccionando Añadir punto. Sin embargo, el software tratará este sector como una sucesión de sectores y no como un sector de curva único. También se pueden introducir coordenadas más exactas importando un archivo de texto. Inclinación inicial define la inclinación del primer punto. Inclinación final define la inclinación del punto final. Puede cargar una spline definida previamente.
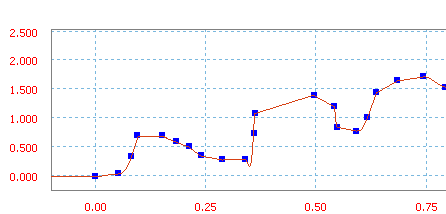
Spline definida mediante adición de puntos
La spline que se ha definido se puede guardar aquí, independientemente de cómo se haya definido. Nota: no se pueden añadir otras leyes a un sector definido por una spline. Además, si reemplaza una ley de sector por una spline, las pendientes iniciales y finales se toman automáticamente de los sectores anteriores y siguientes, aunque esto se puede modificar manualmente más adelante.
Si desea utilizar un archivo de texto que contiene puntos de tangencia, estructure el archivo de la forma siguiente:
// comentarios	Puede incluir una o varias líneas de comentarios en el archivo. Cada línea debe comenzar por “//”. Las líneas de comentarios son opcionales, pero introduzca ahora un valor para que entienda la finalidad de la spline.
[Tangentes] T1 T2	Especifica el valor de la tangente de los puntos inicial (T1) y final (T2) del sector. Estos valores se muestran como inclinación “inicial” y “final” en la interfaz del usuario. Si no se suministra ningún valor, se asume un valor de tangente implícito de 0.0 (tangente horizontal). Al igual que ocurre con las líneas de comentarios, esta línea es opcional, pero como hemos dicho, si no se da ningún valor de tangente, debe asumirse ciertos parámetros.
X₁ Y₁ ... X_n Y_n	La lista de coordenadas de los puntos; se pueden mostrar tantos puntos como sea necesario. Especifique un punto por fila.
Archivo de texto de ejemplo	// // Puntos de simulación de spline de entrada // Valor: Par de la unión (N mm) // Referencia: Tiempo s [Tangentes] -3.40775 -5.27803 +0.000 +0.000 +4.313 +1.510 +7.954 -9.756 +1.000 +0.000
Fórmula	una fórmula en el cuadro de fórmula para definir la curva. Fórmula es una ecuación con funciones y palabras clave. Solo disponible para definir la unión y los esfuerzos externos. No se puede imponer un movimiento en un grado de libertad. La continuidad con los sectores adyacentes no se mantiene de forma automática. El usuario debe definirlos para evitar colisiones durante la simulación. Las fórmulas están limitadas a 255 caracteres. Puede utilizar cualquiera de estas funciones: abs fmod a cos cos log10 sqrt asin sinh log sqr atan sin pow trunk atan2 tanh sign pow10 floor cosh tan sign0 exp round
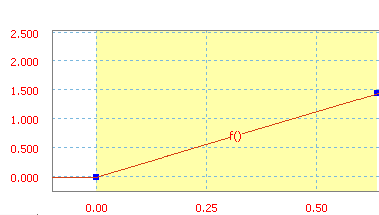
Curva definida por la fórmula Y = X + 37,

Ejemplo 1

Puede crear tres sectores. En el segundo, se necesita un seno de frecuencia baja.

Puede ver la curva antes y después de la creación del seno. El tercer sector se ha desplazado verticalmente para que exista una continuidad entre los dos sectores. Para obtener la curva deseada inicialmente, se deben añadir funciones adicionales.

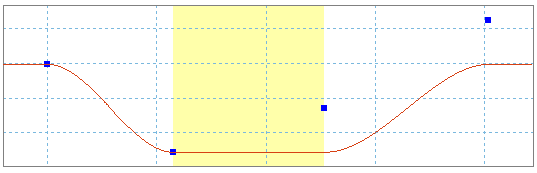
Ejemplo 2

Algunas funciones están limitadas en sus definiciones. Para obtener un seno de variación de 300, se debe añadir una ley constante con un valor de 300 y una ley de seno.

Nota: el orden de la adición a la ley no es importante.

La variación en torno a una pendiente distinta a cero se puede modelar mediante la combinación de un tramo y un seno.

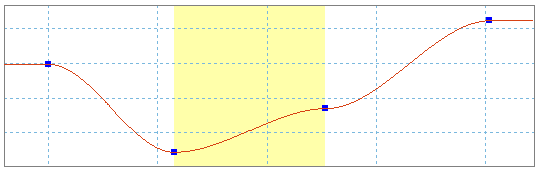
Ejemplo 3

Para simular una vibración en un movimiento alternativo, combine las leyes de seno de diferentes amplitudes y frecuencias.

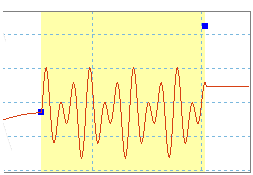
Definición de valores fuera de un sector de curva

Es interesante definir cómo se comportan las variables fuera de los sectores de curva antes y después de la última. Una vez se ha seleccionado un área fuera de toda la curva y se han añadido las condiciones que se desean aplicar, se puede definir el área seleccionada.

Seleccione una definición para el área seleccionada fuera de una curva.
Si selecciona Cíclico, pulse Inicio.
Se abrirá el cuadro de diálogo Selección del punto de inicio.
En el cuadro de diálogo Selección del punto de inicio, pulse la flecha abajo situada a la derecha del campo.
Se abre un menú que muestra cada uno de los puntos que empieza un sector de curva.
Pulse el punto que inicia el sector de curva que desea copiar para esta área.
Pulse Aceptar.

Para definir el área fuera de una curva se dispone de cinco opciones. Son las siguientes:

Valor constante	Esta opción define un valor constante igual al primer valor de la curva si el área se está definiendo a la izquierda del primer punto o el último valor de la curva el área si se está definiendo a la derecha del último punto. Éste es el ajuste por defecto.
Inclinación constante	Esta opción define una línea de inclinación constante en el área seleccionada. El valor de la inclinación es igual al valor de la inclinación del primer sector de curva si el área se está definiendo a la izquierda del primer punto o el valor de la inclinación del último sector de curva si el área se está definiendo a la derecha del último punto.
Módulo	Esta opción define un valor en el rango de definición de la ley (todos los sectores definidos) de acuerdo con el principio de módulo, es decir, una curva que está definida se repite a ambos lados del eje de coordenadas. Simulación dinámica comprueba que la coordenada del último punto de la ley (último sector) sea igual al origen de ordenadas del primer punto (primer sector). De no ser así, aparecerá un mensaje de error solicitándole que modifique los valores. Este mensaje aparece porque el motor de cálculo no puede gestionar las discontinuidades. Este modo se aplica en las piezas situadas a la derecha y a la izquierda de la ley.
Cíclico	Esta función utiliza un ciclo copiado de un punto definido por el usuario hasta el último punto de la curva definida por el usuario. Para el inicio del ciclo, seleccione un punto que sea igual al último punto de la curva definida por el usuario. De lo contrario, se producirá una discontinuidad entre el inicio y el fin del ciclo. En tal caso, aparecerá un mensaje de error.
Libre	Esta opción no establece ninguna definición para el área. No se aplica ninguna fuerza y el grado de libertad simulado (con un movimiento impuesto) se libera. En el caso de un movimiento impuesto, es necesario liberar el sector situado a la derecha del último punto antes de liberar el último sector; después, el penúltimo, etc.