Le curve da equazione consentono di modellare geometrie complesse, ad esempio profili di un dente di un ingranaggio o traiettorie di sweep per pompe idrauliche. Per generare una curva da equazione, specificare le equazioni per definire la curva e un intervallo per valutare le equazioni.
- Nella barra multifunzione fare clic sulla
Scheda Modellazione 3D
gruppo Schizzo
Crea schizzo 3D
. Se è attivo uno schizzo 2D, fare clic con il pulsante destro del mouse e scegliere Concludi schizzo per chiudere l'ambiente 2D. - Nella barra multifunzione fare clic sulla
scheda Schizzo 3D
gruppo Disegna
Curva da equazione
per visualizzare la barra degli strumenti mini.
- Selezionare Cartesiane, Cilindriche o Sferiche per specificare il sistema di coordinate.
- Immettere le equazioni per x, y, z, o r, θ, z o r, ϕ, θ a seconda del sistema di coordinate selezionato.
- Immettere i valori minimo e massimo per t nei campi tmin e tmax.
- Fare clic su OK per creare la curva e uscire dal comando. Fare clic su Applica per accettare la spline e restare nel comando Curva da equazione.
- Aggiungere quote o vincoli tra la curva e gli altri elementi della geometria dello schizzo.
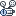Procedura per la creazione e l'uso di curve da equazione
Formato equazione di esempio
Nella tabella seguente sono riportati alcuni esempi di formattazione richiesta per utilizzare alcuni operatori e funzioni.
| Piano cartesiano | Cilindrico | Sferico | |
|---|---|---|---|
|
Addizione/Sottrazione |
x(t): 1 mm * t + 1 mm y(t): 1 mm * t - 1 mm z(t): 1 mm * t - 1 mm |
r(t): 1 mm * t + 1 mm θ(t): 1 rad * t + 1 rad z(t): 1 mm * t - 2 mm |
r(t): 1 mm * t + 1 mm ϕ(t): 1 rad * t + 1 rad θ(t): 1 rad + t - 1 rad |
|
Moltiplicazione/Divisione |
x(t): 2 mm * t y(t): 2 mm / t z(t): 2 mm / t |
r(t): 3 mm * t θ(t): 2 rad * t z(t): 2 mm * t / 2 |
r(t): 3 mm *t ϕ(t): 2 rad * t θ(t): 2 rad / 2 |
|
Esponenti |
x(t): (t^2) * 1 mm y(t): 1 mm * pow(t;2) z(t): 1 mm * pow(t;2) |
r(t): 1 mm * (t^2) θ(t): 1 rad * pow(t;2) z(t): 1 mm * (t ^ (1/2)) |
r(t): 1 mm * (t^2) ϕ(t): 1 rad * pow(t;2) θ(t): 1 rad * (t ^ (1/2)) |
|
Funzioni trigonometriche |
x(t): 1 mm * sin(1 rad * t) + 1 mm * cos(1 rad * t) y(t): 1 mm * tan(1 rad * t) z(t): 1 mm * tan(1 rad * t) |
r(t): 1 mm * cos(1 rad * t) θ(t): 1 rad * sin(1 rad * t) z(t): 1 mm * tan (1 rad * t) |
r(t): 1 mm * cos(1 rad * t) ϕ(t): 1 rad * sin(1 rad * t) θ(t): 1 rad * tan(1 rad * t) |
|
Funzioni trigonometriche inverse |
x(t): 1 mm * asin(t) / 1 rad + 1 mm * asin(t) / 1 rad y(t): 1 mm * atan(t) / 1 rad z(t): 1 mm * atan(t) / 1 rad |
r(t): 1 mm * acos(t) / 1 rad θ(t): asin(t) z(t): 1 mm * atan(t) / 1 rad |
r(t): 1 mm * acos(t) / 1 rad ϕ(t): asin(t) θ(t): atan(t) |
|
Iperbole |
x(t): 1 mm * sinh(1 rad * t) + 1 mm * cosh(1 rad * t) y(t): 1 mm * tanh(1 rad * t) z(t): 1 mm * tanh(1 rad * t) |
r(t): 1 mm * cosh(1 rad * t) θ(t): 1 rad * sinh(1 rad * t) z(t): 1 mm * tanh(1 rad * t) |
r(t): 1 mm * cosh(1 rad * t) θ(t): 1 rad * sinh(1 rad * t) ϕ(t): 1 rad * tanh(1 rad * t) |
|
Logaritmica |
x(t): 1 mm * ln(t) y(t): 1 mm * log(t) z(t): 1 mm * log(t) |
r(t): 1 mm * log(t) θ(t): 1 rad * ln(t) z(t): 1 mm * ln(t) |
r(t): 1 mm * log(t) ϕ(t): 1 rad * ln(t) θ(t): 1 rad * ln(t) |
Modifica curve 3D da equazione
Modifica dell'equazione per modificare la curva. Usare le quote e i vincoli per controllare la posizione della curva.
Per modificare una spline 3D in uno schizzo 3D attivo, usare una curva da equazione:
- Fare clic con il pulsante destro sulla curva nella finestra grafica o nel browser, quindi selezionare Modifica curva da equazione per visualizzare la barra degli strumenti mini. È possibile modificare le equazioni, modificare il sistema di coordinate, oppure modificare l'intervallo.
- Aggiungere vincoli per controllare le relazioni tra la curva e un'altra geometria. Le curve di equazione supportano vincoli coincidenti, tangenti, perpendicolari e fissi.
- Aggiungere una quota tra il punto finale della curva e altri elementi di geometria.
- Fare clic col pulsante destro del mouse sulla curva e scegliere Visualizza curvatura per analizzare la curvatura della curva da equazione.