長繊維複合材料を使用した繊維配向解析の実行において、繊維破断を計算するオプションが導入されました。
導入された繊維破断モデルは、Phelps および Tucker [1] によって、流動場の座屈およびせん断力による繊維破断の確率を表す統計モデルとして初めて提案されました。
単一のファイバーの流体力による破断確率は、次の式で求めます。
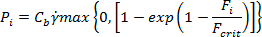
ここで、力比は、Dinh および Armstrong [2]によって表される流体圧縮力に対するクリティカル座屈力です。次のように示されます。
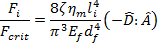
ここで、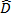 
、および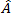 
は、それぞれ変形速度テンソルと繊維配向テンソルです。その他の変数は、抵抗係数である 
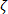以外は、ファイバーとマトリックスのプロパティです。
ファイバーは、破断しているいないにかかわらず、流動場で消失または成長できないため、保存則に従います。保存則は、次の式で表します。
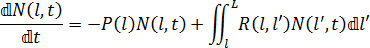
ここで、L は初期ファイバー長、N(l,t) は t のときの長さ l のファイバーの数、P(l) はファイバー長 l のスカラー確率関数、R(l,l') はファイバー長 l が破断して、ファイバー長 l' (ここで、'<l)を形成する確率関数です。次のように、ガウス破断プロファイルとして表すことができます。
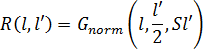
ここで、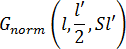 
は、平均 l'/2 および標準偏差 Sl' の変数 l に対するガウス正規確率密度関数です。S は無次元のフィッティング パラメータで、ガウス破断プロファイルの形状を制御するのに使用できます。
参考資料
- Phelps, J.H., Processing-microstructure Models for Short- and Long-fiber Thermoplastic Composites. Ph.D. thesis, University of Illinois at Urbana-Champaign (2009).
- Dinh, S.M. and Armstrong, R.C., A Rheological Equation of State for Semi-Concentrated Fiber Suspensions. J. Rheol., 28(3):207-227 (1984).