繊維配向予測の理論的基礎

金型充填時の 3 次元繊維配向の数値的な予測は、懸濁液における剛体粒子の運動方程式に基づきます。

解析は、特定可能な次の 2 つの項で構成されます。

• 流体力学項
• 相互作用項

粒子の運動に対する流体力学的な影響は、無限アスペクト比を仮定した Jeffery の方程式で記述されます。この理論は、厳密には希薄懸濁液に適用されるものですが、実験データと質的に一致するという利点を示すために提示されました。

相互作用項は、Folgar および Tucker によって提案されました。この項は、機械的な繊維相互作用によるランダム化の影響をモデリングすることを目的として組み込まれました。この項の形式は、歪速度の大きさに比例する相互作用頻度を拡散項に追加したものです。相互作用項の効果は、一部の流動条件に対して、Jeffery のモデルで予測される整列度が高い配向状態が低減され、実験の観察結果との整合性が高まることです。

繊維配向の定義と予測

3 次元繊維配向の計算は、同じ有限要素メッシュに対する金型充填解析と並行して実行されます。各三角形要素は、局部的な成形の肉厚を分割する複数の層で構成されると考えることができます。各レイヤーは、そのレイヤーが通るグリッド点によって識別されます。成形の中間面はグリッド点 1 を通ります。メッシュ内の各要素の各レイヤーで、配向の解が計算されます。それによって、成形の断面を通って金型表面と平行する、一連の平面上の配向分布のばらつきを観察することができます。

各要素の 3 次元配向の解は、2 次テンソルによって記述されます。グラフィックな表現のために、配向テンソルの固有値と固有ベクトルが生成されます。固有ベクトルは繊維の整列の主方向を示し、固有値はその方向に整列している繊維の統計的な比率 (0～1) を示します。この情報に基づいて、各要素に対する繊維の整列の分布を完全に記述する、配向楕円体が定義されます。次の図は、一般的な配向楕円体を示したものです。

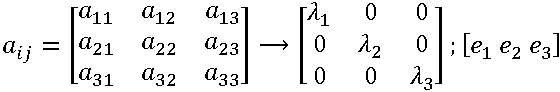
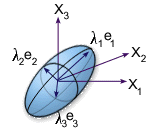
表示目的で、この 3D 楕円体は各要素の平面上に投影され、平面楕円が生成されます。これにより、配向分布の便利な表現方法が得られます。なぜなら、投影によって除去されるギャップ方向の配向成分が、通常小さいためです。この表現方法では、ほぼランダムな分布は、円に近い楕円として表示されます。それに対し、整列度が高い分布では、楕円は線状になります。

配向テンソルの記述

2 次配向テンソル、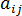 は射出成形における繊維配向を効率的に記述します。このテンソルは 9 個の成分で構成されます。これらのテンソル項の添え字は次の方向を表します。

• 流動方向
• 流動に対して横方向
• 肉厚方向

通常、次の軸が該当します。

• XY (または 1-2) 流動面
• 1-2 流動面外にある、肉厚方向の Z 軸

元の 9 つの成分は、次の条件により、5 つの独立した成分に縮約されます。

• テンソルの対称性 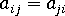、および
• 正規化条件

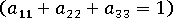
配向の検討では、次の 3 つの主要配向成分が考慮に入れられています。

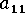• 流動方向の繊維配向(0～1.0)
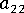• 流動に対して横の方向の繊維配向(0～1.0)
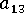• 1-3 平面における配向の傾き(-0.5～0.5)

注: 流動方向配向の項、 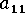には、ミクロ構造に関する定量的な情報のほとんどが含まれます。この項は、流動、処理、および材料の変更による影響を非常に受けやすい項です。

繊維配向モデル

対象の複合材料を、粘性媒体内に分散する粒子またはファイバーと考える場合があります。ファイバー間には、機械的または流体力学的な相互作用が存在します。

懸濁液には、次に示す、希薄懸濁液、中濃度懸濁液、および高濃度懸濁液が存在します。

• 希薄懸濁液では、ファイバーどうしが接近せず、相互作用は発生しない。

• 中濃度懸濁液では、機械的な繊維相互作用はありませんが、流体力学的な相互作用が顕著になる。

• 高濃度懸濁液では、機械的と流体力学的の両方の繊維相互作用が関与するため、繊維配向の挙動が非常に複雑化する。

Jeffery は、まず、大量の非圧縮性ニュートン流体内に浮遊する、単一のファイバーの運動をモデリングしました。Jeffery のモデルは、非常に希薄なために、繊維相互作用(流体力学的相互作用を含む)を無視できる懸濁液にのみ適用されます。

懸濁濃度を評価する重要な指標の 1 つとして、ファイバー間の平均距離があります。

直径(d)、長さ(L)、アスペクト比(L/d)、体積によるファイバー濃度(c)(または体積率 )、および長さの分布が均一なファイバーについて考えた場合、一般的な濃度分類スケールは次のようになります。

• 希薄c << (d/L)²
• 中濃度 (d/L)² < c < (d/L)
• 濃厚 c > d/L

例: L/d が 10 (複合材料での繊維強化の小さい値)の場合、Jeffery の式を適用するには、ファイバー濃度が体積比 1% よりはるかに希薄でなければなりません。

市販材料の場合、ファイバーのアスペクト比 L/d は一般に 20 以上であるため、上記の濃度の値は次のようになります。

• 希薄 c << 0.025
• 半濃厚 0.0025 < c < 0.05
• 濃厚 c > 0.05

これらの分類スケールの区切り値を重量比で表した場合、通常、約 0.5% と 10% に換算されます。

多数の市販複合材料には、重量比で 10～50% のファイバーが添加されています。このようなファイバーは、高濃度懸濁液と考えることができます。

中濃度懸濁液用には、Dinh と Armstrong によってモデルが提案されています。繊維配向は、粒子が伸張しない点を除いて、流体の体積変形に従います。

高濃度懸濁液用には、項「相互係数」() が、Folgar と Tucker が提案した繊維配向の現象論的モデルに組み込まれています。

• 繊維間の相互作用は、配向をランダム化する傾向にあります。
• この項は拡散項と同じ形式をとる。相互作用は懸濁液の変形時にのみ発生するため、有効拡散係数は歪速度に比例する。
• 無次元の の項は、拡散項の強度を決定します。

繊維相互作用を考慮するための回転拡散項を追加すると、配向予測の精度が向上することがわかっています。これは、Jeffery の式だけでは、質的に正確な繊維配向予測が得られないためです。

これまでのところ、Folgar-Tucker モデルは、高濃度懸濁液における繊維配向のモデリングに使用できる最適なモデルです。このモデルは、Advani と Tucker によって次の形式で提案されました。

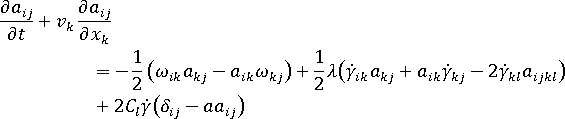
ここで、

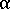• は、3D 配向では 3、より平坦な(2D)配向では 2
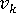• は速度成分
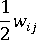• は渦度テンソル、 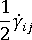は変形速度テンソル
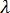• は粒子の形状に依存する定数
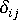• は単位テンソル
• は相互係数

繊維配向モデルの完結

Advani と Tucker の繊維配向モデルのテンソル形式は、4 次テンソル 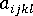が含まれているため、まだ 2 次配向テンソルの適切な導関数とはなっていません。

4 次テンソルの導関数には、6 次配向テンソルが含まれます(以下同様)。したがって、適切な導関数を得る唯一の方法は、4 次テンソルを 2 次テンソルの観点から近似化することです。

この近似化を「完結近似」といいます。""Advani と Tucker によって、さまざまな近似化がテストされています。しかし、近似化それ自体の存在によって、シミュレーション結果に何らかのエラーが発生する可能性もあります。そのため、完結近似は、このモデルに関連する最も困難な問題となっています。相互係数、 の値で、繊維配向モデル式を、配向モデルのすべての成分に適合させることができる値はありません。

Advani と Tucker による繊維配向モデル形式を検討することにより、繊維配向予測の精度を決定する、次の 2 つの方法が提示できます。

• より精度の高い完結近似を見つけ出す方法

• 完結近似エラーを考慮した新しい相互作用モデルを見つけ出す方法

最初の方法が望ましいと考えられますが、数十年に及ぶ の範囲に対して、せん断流動と伸張流動の範囲を満足にカバーする完結近似は見つかっていません 。

完結近似の効果は、過度の面外配向を予測できることです。この結果には、Autodesk 提案の繊維配向モデル形式が対応しています。