Moldflow 繊維配向モデルは、Folgar-Tucker 繊維配向式に基づいています。
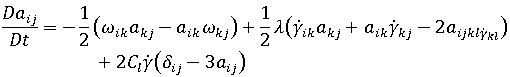
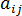は繊維配向テンソル 
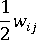は渦度テンソル、 
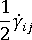は変形速度テンソル 
は 繊維相互作用係数というスカラー現象論的パラメータで、実験結果へのフィッティングにより求める値。この項は、繊維間相互作用を説明するために、元の Jeffery 式に追加された。
)という追加の項が導入されています。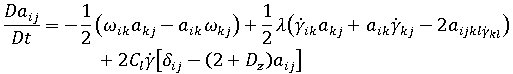 
この改良モデルには、次の仮定および考慮がなされています。
-
Folgar-Tucker モデルを使用すると、高濃度懸濁液における繊維配向の予測に関して、許容可能な精度が実現できる。
-
簡単な形式で動的挙動が良好であるため、ハイブリッド完結近似を使用する。
次の点に注意してください。
- 設定 = 0.0 と設定すると、モデルが元の Jeffery 形式に設定されます。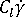
は繊維配向テンソルに影響する。 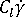= 0 である場合、遷移間の相互作用はなく、 の値が非常に大きくなると、繊維配向は低くなります。 - 項の大きさは、繊維相互作用による、面外方向へのランダム効果の影響度を設定します。
- 設定 = 1.0 と設定すると、3D 問題に対応する Folgar-Tucker 配向モデルが与えられます。設定 = 0.0 と設定すると、2D 問題に対応する Folgar-Tucker 配向モデルが与えられます。
ただし、射出成形では、樹脂流動の流体力学により、ファイバーは主として流動面内に存在します。ファイバーが面外に回転する可能性は、著しく制限されます。このメカニズムにより、繊維配向のランダム効果は、面内方向よりも面外方向の方が大幅に小さくなり、 は低い値になると予測されます。
- この パラメータを小さくすると、次のようになります。
- 面外配向が減少する。
- コア層が厚くなる。
- シミュレーションでは、この問題を、中間面に関して対称的であるとして処理する。
実験式 とスケール変更された体積率の式の比較
Bay の実験的研究では、Folgar と Tucker の相互作用モデルが、射出成形の問題に適用できることが示されています。しかし、どの 値を繊維配向モデルに適用すればいいのかという疑問が残ります。
Folgar と Tucker の実験は、 はファイバーの体積率とアスペクト比に依存することを示しています。しかし、依存性の詳細は不明でした。
フィルム ゲートを使用したストリップにおける流動は、主に単純せん断です。シェル層(中間面から壁までの 40～90% を占める)では、単純せん断に対して定常値を取ります。この状況から、上記の依存性を適切に調べる方法が導き出せます。
Bay のシェル層配向の結果は、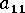 
がファイバー濃度の影響を受けやすく、相互係数に関する実験的な関係式を構築できることを示しています。また、Bay の測定結果は、歪速度に比例する速度でファイバーが拡散するという提案を裏付けています。
Bay の論文には、ファイバー細部に対する相互係数 の依存性に関して、実験関係式が提案されています。この式は、単純な指数関数的な 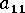項です。データは、さまざまな材料 (PC、PBT、PA66) の射出成形されたストリップのシェル レイヤーから、材料ごとに 6～7 のガラス レベルで得られます。すべてのケースを、高濃度懸濁液と見なすことができます。
修正された実験式 式
シェル層の配向の結果に基づき、さまざまなガラス成分を対象に、Bay の式から得られた既定値 の適用範囲が見直されました。
条件 = 1.0 (Folgar-Tucker モデル形式)で、 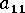配向が、両材料のすべてのガラス含有量に対して、過大予測されています。ガラス含有量が増加するにつれて、過大予測のレベルは低下します。下図を参照してください。
端部でゲート処理されたストリップと中央でゲート処理されたディスクの両方を使用して、一連の繊維配向充填+保圧解析の検証を実行しました。2 つの材料(PA66 と PBT)について、さまざまなガラス含有率で、ストリップのシェル層 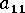配向に関する詳細な検討を行い、その結果を Bay の実験的な配向データと比較しました。配向レベルは、ほぼ 0.8 でした。
修正された実験式 (スケール変更された体積率 cL / d に対するもの。 = 0.01 および 1.0)は、保圧過程の結果を使用して導かれました。
中間値 には、より複雑な手順が適用されます。
下図は、次のような場合における、両材料のさまざまなガラス含有率での、シェル層 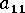の配向予測の誤差を示しています。
- = 0(Jeffery モデル)。
- Bay の経験式 ( におけるもの。 = 1.0 の場合(Folgar-Tucker モデル))。
- 一般的な射出成形品(成形品肉厚 <; 2.5 mm)については、修正された のモデル( の値が低い。 過去に提案された既定値が = 0.01 など)が下図に表示される。
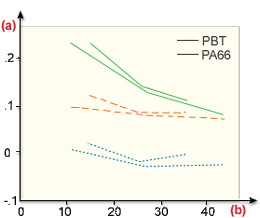
改訂版
. のモデル( の値が低い)(a) エラー; (b) % ガラス(重量);
= 0.0 (Jeffery モデル); 
Bay ( = 1.0); 
Moldflow モデル (= 0.01) - 厚肉成形品(肉厚 > 2.5 mm)については、修正された モデル( = 1.0)が使用される。 の値は、成形品の肉厚とともに単調に増加することが示されている。この増加傾向は、面外の繊維配向が成形品肉厚の増大に伴い増加する、という予想と一致している。
次のような観察結果が得られます。
- Jeffery モデルと Folgar-Tucker モデルは、配向評価が過大予測される傾向がある。
- 薄肉成形品(肉厚 < 2.5 mm)の場合、 値が低いモデルでは、誤差レベルが大幅に低下する。
- 既定の Bay モデル( の値が低い)では、ガラス含有率が高い場合を除き、Bay の実験データの信頼帯内にある配向評価が得られます。
- 修正されたモデルでは、両材料およびすべての検討したガラス レベルに対して、他のモデル ケースの場合より配向予測が大幅に向上する。
サマリー( ): の組み合わせ
相互係数 の有効なデータ範囲は、0～-1.0 です。ただし、0.1 より大きい値を使用しても、実験結果と比較して、予測が向上しないことが判明しています。
肉厚モーメント相互係数 の有効なデータ範囲は、0.0001～1.0 です。
下表に、このソフトウェア リリースで許容可能な、相互係数と肉厚モーメントの組み合わせの概要を示します。
| 相互係数、 |
肉厚モーメント相互係数、 |
コメント |
|---|---|---|
| 0 | 0.0001–1.0 |
|
| 0 < <= 0.1 |
1.0 | Folgar-Tucker モデル |
| 既定の | = 1.0 (既定 = 1.0) |
は、機械的特性の項を使用して、スケール変更された体積率(cL / d)に従って、実験式から算出されます。
< 0.01 |
| ユーザ セット (0–0.1) |
<= 1.0 (既定 = 1.0) |
他の実行が許可される。 |
繊維配向の解析スキーム概要
成形プロセス中、ある点の繊維配向は、流動から推定される配向(運動力学項)および対流流動による配向(移流項)という、2 種類の流体運動に支配されます。
運動力学項では、予測の精度は、計算された速度勾配の精度に依存します。
移流項では、その精度は、配向勾配の計算に依存します。速度と同様に、配向テンソルの表現も、座標系に依存します。速度勾配の計算に適するすべての数値スキームを使用して、配向勾配を計算することができます。繊維配向ソフトウェアでは、同じ要素システムを使用して、速度場および配向場を表します。したがって、同じスキームを使用して、速度勾配と配向勾配を計算します。
繊維配向スキーム全体の概要を、ここで説明します。繊維配向予測は、金型充填シミュレーションと組み合わせて使用されます。
まず、充填と繊維配向の計算に関して、アルゴリズムが初期化されます。
次に、すべての要素が固化するまで、次の解析ループが繰り返されます。
- 充填 + 保圧解析に対する、タイム ステップ
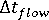の指定 - フロー フロントの前進
- 圧力場と速度場、および歪テンソルの計算
- 移流項に対する、安定したタイム ステップ
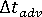の計算 - タイム ステップの繰り返し(
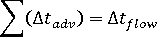になるまで) - 各要素の各グリッド点に対して、次の計算を行う。
- 移流繊維配向項の計算(
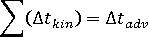になるまで) - 運動力学繊維配向項の計算
- タイム ステップ
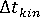の計算(運動力学項に対する) - タイム ステップ 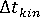の間の新しい繊維配向の計算
- 移流繊維配向項の計算(
- ループの始めに戻る。