不安定な反りは、構成部品の座屈の発生要因となります。総変形に対する 3 つの収縮変量のそれぞれの寄与分は、線形であるとは仮定できません。
この場合は、感度解析と呼ばれる解析を使用します。この機能は、Midplane 解析でのみ利用可能です。
感度解析の目的は、既知の収縮変化によって発生する荷重係数の変化を知ることにあります。荷重係数は、実際にかかる荷重の何倍の荷重で成形品に不安定な反りが発生し始め、座屈につながるかを示します。収縮解析では、これらの荷重は成形品の内部荷重です。荷重係数が 1 を下回ると、実際の荷重で成形品に座屈が生じることになります。荷重係数が 1 より大きければ、実際の荷重よりも大きい荷重で座屈が始まると判断できるので、反りは安定しています。
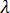は次のように、これらの成分の関数とみなすことができます。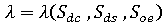 
反りの問題を解決するには、荷重係数を高くして安定した反りとするために、どの成分を変更すればよいかを知る必要があります。この方法として、収縮成分ごとに 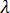の偏導関数を導く手法があります。残念ながら、解析手法でこれを達成することはできません。 これは、 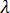を収縮成分に関連付ける既知の関数は存在しないためです。代替手段として、この偏導関数を近似化することにします。
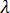であるとします。ここで、収縮成分のいずれかを 
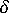だけ増加させ、総収縮量を S とします。たとえば、収縮差成分を増加させ、次のようにします。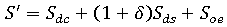 
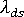を得ると、収縮差成分に関する 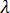の導関数は次のように近似化できます。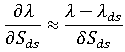 
GUID-7C213889-592D-4D06-A497-53C28068D4C7.htm#FIG_FF650406D7984218B7EBA1637CABB2A0 を参照してください。
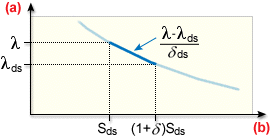
収縮の関数としての荷重係数
.(a): 荷重係数、(b): 収縮
この説明では 1 つの要素のみを扱っています。実際の成形品では、それぞれの要素に値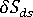 
が存在します。これを処理するには、要素に発生する変化を、収縮変化を表す単一の指標に組み込みます。要素収縮に変化のノルムを使用して、単一の値を取得します。
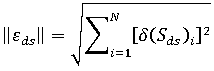
ここで N は、モデルの要素数です。
値(1 + 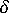)は感度ファクターと呼ばれ、プログラムへの入力値となります。
冷却差変量と配向の影響変量についても、同様に荷重係数の感度を計算します。