多点拘束

注: このセクションの情報は、線形構造解析、熱解析、および静電解析に適用されます。

多点拘束(MPC)は、その解析において異なる節点や自由度を結びつけることができる拡張機能です。この機能は正則境界状況が正確な動作を提供しない場合に、境界条件効果をシミュレートするのに頻繁に使用されます。

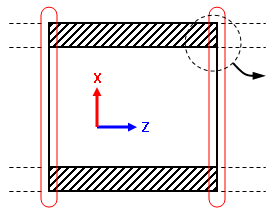
MPC の 1 つの使用法としてマスタ スレーブ関係があります。: 節点 X(スレーブ節点)においての変位は、節点 Y(マスタ節点)における変位と同じである必要があります。図1では、長いベッセルの一部がモデルとなっています。左の辺は、対称性境界条件を使用しています。これは、z 平行移動のモデルを拘束し、左側のタンクの一部をシミュレートします。長いベッセルに関しては、モデルの右側のタンクの一部は節点が 1 つの個所に留まるようにします。対称性境界条件は、節点がタンク内で軸方向成長や縮小を妨げる以外はうまく機能すると思われます。代わりに、MPC は、節点すべての Z 変位が等しい(必ずしも 0 でない)ことを示すのに使用されます。同様に、熱解析の温度および静電解析の電圧は MPC の基準にすることができます。

詳細:

Z 対称条件は左の面を拘束します。節点は Z 方向へ移動します。

MPC 条件は 1 つの個所に留まるように右の面を拘束します。つまり、節点は Z 方向へ共にに移動します。

MPC やその他の境界条件がない場合、右面の節点は荷重のため自由に偏向します。これはベッセルの一部を正確にシミュレートせず、解析には盛り込まれません。

図1: 多点拘束の使用

注: 線形解析タイプの中で多点拘束は、線形材料による静解析、固有値解析、過渡応答解析(直接積分)の解析タイプでのみ使用できます。応答スペクトル解析やランダム応答解析など、モーダル解析の結果を使用する線形解析タイプの場合、MPC の効果が盛り込まれた結果が生成されます。熱解析の場合、MPC は定常熱伝導解析と非定常熱伝導解析の両方で使用できます。同様に、静電解析の両方のタイプ、つまり静電電流と電圧解析および静電界強度と電圧解析も MPC をサポートします。

多点拘束の入力値は、以下の形式の方程式です。

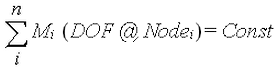
ここで、

この方程式に単位が含まれる場合は、モデル単位を用いて表記します。MPC 方程式は表示単位は使用しません。

MPC 方程式の入力

  1. FEA エディタで、MPC 方程式に必要な頂点番号と関連する DOF を書き留めます。頂点番号を取得するには、[選択][選択する][頂点]で頂点を 1 つ選択し、右クリックで[照会]を選択します。(または、対象の頂点上でマウス ポインターをしばらく静止させ、ツールチップでプロパティを表示します。)
  2. サポートしているすべての解析タイプでは、リボンの[セットアップ]タブに[多点拘束]コマンドがあります。
    • 線形構造解析の場合、このコマンドは[拘束]パネルのプルダウン メニューで選択できます。
    • 熱解析の場合、このコマンドは[熱荷重]パネルのプルダウン メニューで選択できます。
    • 静電解析の場合、このコマンドは[荷重]パネルのプルダウン メニューで選択できます。
    モデル上で何も選択されていない状態で表示領域を右クリックし、[追加] [多点拘束]を選択することもできます。[多点拘束を定義]ダイアログ ボックスで、前述の方程式の項をすべて入力します。
  3. [追加]ボタンをクリックし、拘束方程式を新規で作成します。ここで、方程式名は自動で入力されます。または、[方程式名]ドロップダウン メニューより既存の方程式を選択し、編集を行います。
  4. [定数]フィールドで方程式の定数を指定します。(上記方程式の Const へ)
  5. [行を追加]ボタンで、方程式の各項の指定に必要な数の行をスプレッドシートに追加します。各行に[乗数]、[頂点 ID] (ステップ 2 で書き留めた頂点番号)、および適切な[DOF] (自由度)を入力します。線形解析の場合、ドロップダウン リストから値を選択できます。熱解析と静電解析の場合、DOF はそれぞれ[温度]と[電圧]に固定されます。
    注: 頂点がローカル座標システムへ割り当てられた場合、選択されたDOFもローカル座標システムにあることになります。例えば、X 平行移動は円筒座標システムにおける径方向並進移動を示し、Y 平行移動は接線方向を示すなどです。
  6. [解析手法]を選択し、[ペナルティ乗数]を設定します(ペナルティ乗数はペナルティ法で使用されます)。次の解析手法から選択できます。
    • [自動]
    • [ペナルティ法]
    • [縮合法]
    注: ペナルティ乗数の推奨値は、それぞれ[設定]トピックから見つけることができます。このトピックへスピーディーにアクセスするために、[ペナルティ乗数]検索を行います。
    注: [多点拘束を定義]ダイアログ ボックスで選択した解法は、MPC を含むすべての機能で使用される解法になります。これらの機能には、周期対称、摩擦なし拘束、スマート接着、ユーザ定義の MPC などがあります。たとえば、ペナルティ法を使用して、スマート接着に関連するすべての解析の解を求める場合、[多点拘束を定義]ダイアログ ボックスで[ペナルティ法]を選択して、既定の縮合法をオーバーライドすることができます。
  7. [OK]ボタンをクリックして、ダイアログ ボックスを閉じます。
  8. 解析を実行します。

互換性に関する注意事項: バージョン 20 から 20.4 P1 まで

バージョン 20 から 20.4 SP1 でMPC データを保存するために使用した入力内容に関しては、すでに互換性はありません。旧バージョンの入力内容を回復するには、設計シナリオ フォルダ(例えば、モデル名.ds_data\1)内にある DS.CST.BAK ファイルを編集します。以下より旧式の MPC 方程式が使用できます。節点番号は対応する頂点番号へ変換する必要があります。方程式は[追加][多点拘束]より再度入力が必要です。.CST.BAKファイルの形式は次のとおりです。

#_equations、max_n

2 つの数字: ファイル(#_equations)内の方程式の数と、いずれかの方程式の最大項数(max_n *方程式が等しい定数は数えません)2 つの数字は整数でなくてはなりません。

#_terms(1)

方程式 1 内の項数項数は整数でなくてはなりません。

node(1)、DOF(1)、M(1)

node(2)、DOF(2)、M(2)

node(3)、DOF(3)、M(3)

node(#_terms)、DOF(#_terms)、M(#_terms)

一行あたりの3つの数字と数字の#_terms 行3つの数字は節点数(節点(i))、節点における自由度(DOF(i))、項の乗数(M(i))です。乗数は実数で、その他の数字は整数でなくてはなりません。DOF(i)の有効な数字は以下の通りです。

1 = X 並進

2 = Y 並進

3 = Z 並進

4 = X 回転

5 = Y 回転

6 = Z 回転

定数(1)

方程式 1 の定数値この数字は実数でなくてはなりません。(1 の代わりに 1.00 または 1.0E0)

 

上記の3つの行 [#_terms; node(i), DOF(i), M(i); Constant] は、それぞれの MPC 方程式で繰り返します。(2 から #_equationsにかけて)

例

図2の歯車を解析します。回転連結を模擬化するためビーム要素で歯車のモデリングする代わりに、多点拘束を使用します。この歯車では、半径 1 * 回転 2 = - 半径 2 * 回転 2つまりMPC 方程式は、半径 1 * 回転 2 + 半径 2 * 回転 2 = 0ここでの寸法、頂点数では、MPC への入力値は以下のようになります。

方程式 1

定数 = 0

乗数

頂点 ID

DOF

3

12

X 回転

9

18

X 回転

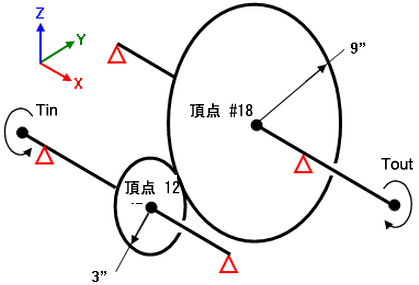
図2: ビーム要素で解析された歯車

親トピック: 荷重および拘束