Mooney-Rivlin 材料モデルは、超弾性材料モデルです。2D、ブリック、4 面体、膜、シェル要素で使用できます。Mooney-Rivlin 材料特性を次に示します。これらの特性に加えて、一部の等方性材料特性の定義が必要になる場合があります。
カーブ フィッティング ルーチンを使用するには、[要素の材料指定]ダイアログの[カーブ フィット]をクリックします。このルーチンによって、計測済みの応力-ひずみデータを使用して材料定数が計算されます。
この材料のポテンシャル関数は次数に応じて次のようになります。
2 定数の標準関数:
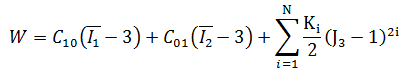
5 定数の高次関数:
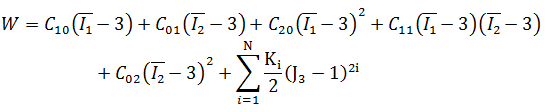
9 定数の高次関数:
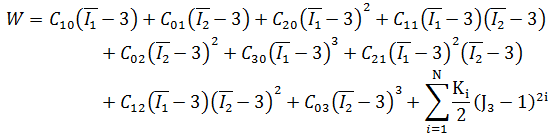
次数に関係なく、初期せん断係数 µ0 および体積弾性率 k0 は、次のように次数 N=1 の多項式係数によってのみ決定します。
μ0 = 2(C10 + C01) , k0 = K1
Mooney-Rivlin 形式は、左 Cauchy-Green テンソルの第 2 不変量に応じて項を追加する点において、Neo-Hookean 形式の拡張と考えることができます。この形式は、Neo-Hookean 形式よりも実験データへの適合精度が高くなる場合があります。ただし、どちらのモデルも不変量の線形関数しか使用しないため、一般的に精度はほぼ同程度になります。これらの関数は、応力-ひずみ曲線における比較的高いひずみレベルの「上昇」を表現することはできません。
体積弾性率
体積弾性率は、E/3*(1-2)という式から求められます。E は材料の弾性率、v は材料のポアソン比です。
最初および 2 番目の定数
Mooney-Rivlin 式 sigma=2(C1 + C2/lambda)(lambda-1/lambda^2) は、sigma/(2(lambda-lambda^(-2)))=C2+lambda^-1+C1 という形式に置き換えることができます。この式は、y=mx+b という形式の線形表現に相似します。m は、2 番目の Mooney-Rivlin 定数 C2 に対応する傾きで、b は、最初の Mooney-Rivlin 定数 C1 に対応する y 切片です。(上記の高次の材料モデルおよびポテンシャル方程式は最初の定数 C10 と 2 番目の定数 C01 を参照します)。