鉄筋コンクリート材料モデルは、引張と圧縮の動作が異なり、統計的に均一であるとして扱われます。個々の肉眼で確認できる亀裂を追跡するのではなく、統合点の弾力性の変性によって亀裂や破砕をシミュレーションする、塗布亀裂モデルに従います。ここで説明するモデルは、比較的単調な載荷を対象としています(真の単調載荷は増加するまたは減少しますが、元に戻ることはありません)。現在のモデルでは、亀裂は最も重要な点と見なされますが、封じ込められた中の圧縮も正当に考慮されます。
鉄筋コンクリート材料モデルも、塗布鉄筋手法を実装します。鉄筋は、指定した容積の割合を持つ要素全体に分布していると想定されます。 鉄筋の強度は、指定された方向のコンクリートを強化します。鉄筋材料は、フォンミーゼス等方硬化の弾塑性材料モデルに従います。鉄筋の 3 つの独立した方向を定義できます。
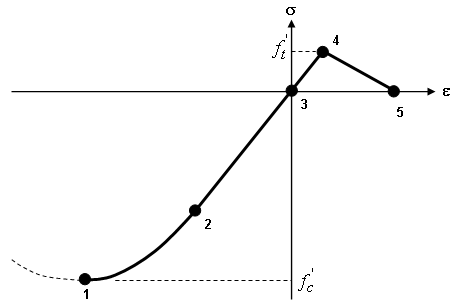
図 1 は、平面コンクリートの通常の一軸挙動を示します。コンクリードが圧縮の負荷をかけられると(ポイント 3-2-1)、降伏点(ポイント 2)に達するまで弾性的に動きます。材料は柔らかく反応し、回復不可能な変形が発生します。ピークの強度(ポイント 1)で破壊点に達した後、材料は劣化しますが、理論的にはいくらかの負荷に耐えることができます。この圧縮の軟化は現在解析によってモデル化されておらず、コンクリートには亀裂が入り、このポイント移行は負荷に耐えることができないと見なされます。破壊前に負荷をなくすと弾性があると見なされ、ヤング率に従います。
コンクリートが張力の負荷をかけられると、破壊点(ポイント 4)に達するまで弾性的に動きます。破壊後の張力の挙動は、鉄筋コンクリートの亀裂間の負荷の移行(引張硬化 )のモデル化において非常に重要です。
|
|
| 図 1: 平面コンクリートの理想的一軸挙動 |
破壊の基準
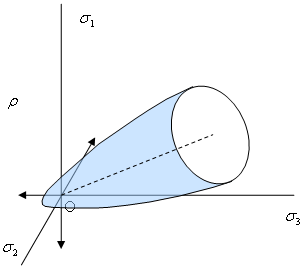
Haigh-Westergaard 座標(x、r、q)によって圧力の状態が定義される、主要なな応力空間で作業する場合に役立ちます。
|
|
ここでは、I 1 =δ ij σ ij 、J2=0.5S ij S ij 、J3=(S ij S jk S ki )/3 および S ij =σ ij - (δ ij σ kk )/3 です。
|
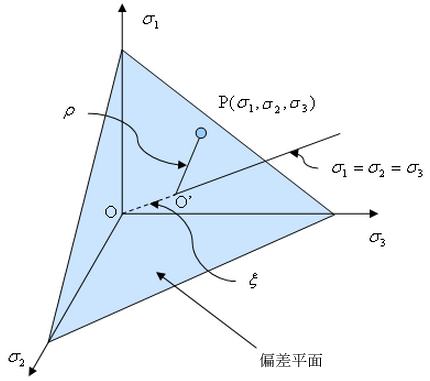
(a) 主要な応力空間 |
|
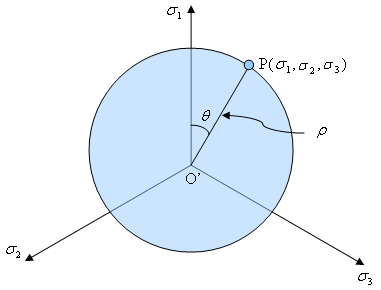
(b) 主要な圧力が投影された偏差平面 |
| 図 2: Haigh-Westergaard 圧力座標 |
解析では、Hsieh-Ting-Chen (HTC)の 4 つのパラメータ基準(参考 1)に類似した破壊基準を使用しますが、依存性の効果がWillam と Warnke(参考2)の偏差半径の表示を介して導入されています。
|
|
|
|
ここでは、f t ' および f c ' はそれぞれ一軸引張力と圧縮力(絶対値)です。e は Kang and Willam で定義された偏心度です。
|
|
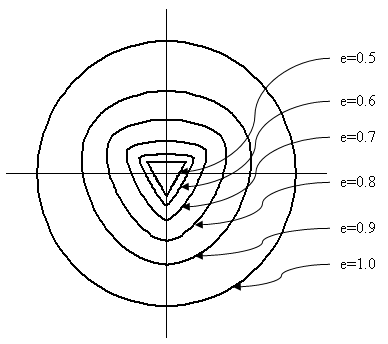
c 0 は、実験で測定できる材料定数です(Kang and Willam では 5.5 に設定されています。参考 5)。 等 3 軸引張強度は ζ 0 =sqrt(3)f t ' です。 1 の偏心度は偏差平面(図 3)で、破損はロード角ϑからは独立しています。
収量面の負荷は、単一のパラメータkを介して初期降伏曲面から最終的な破壊のサーフェスへ拡張すると仮定されます。値の範囲は、初期降伏曲面の 0 から破損面の 1 です。Imran および Pantazopoulou に従い(参考 4)、静圧軸を持つ中間破損面は追加の条件によって制御されます。
|
|
また、解析では限界引張(最大引張応力または Rankine 基準)の導入による、引張が支配的な状態に対する降伏がないと仮定しています。張力と圧縮が混在した領域(参考 1)では、降伏面が徐々に展開します。破壊包絡線は、図 3 で示したように主な応力空間で開いたサーフェスです。解析では、破壊は引張主応力が存在する場合の亀裂であると常に仮定します。コンクリートが複雑な状況で破損しているためあいまいであり、結果として検証しても破損タイプを判断できません。
|
(a) コンクリートの破壊包絡線 |
|
(b) コンクリートの破壊包絡線の偏差表示 |
| 図 3: コンクリートの破壊包絡線 |
圧縮効果
簡単に説明すると、コンクリートに顕著な圧縮荷重が掛けられている場合、関連する流体および等方性歪み硬化が使用されます。この方法は、対称な支配方程式を生成し、計算効率が高くなります。ただし、通常はプラスチックの体積の歪みを過大予測します。
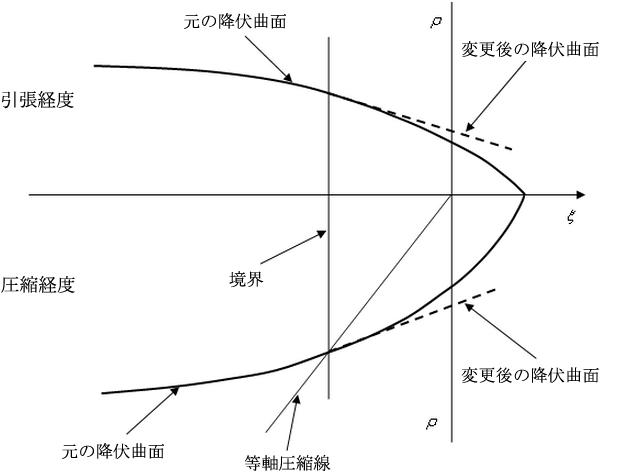
張力と圧縮が混在する領域では(参考 1)、降伏曲面が境界の元のサーフェスに対して正接面となるよう変更されます。
|
|
| 図 4: 張力と圧縮が混在する領域の降伏曲面 |
圧力の更新は、多くの計算を必要とする完全な暗黙的な後退 Euler 法の戻り値のマッピング方式を使用します。
引張硬化
亀裂は、少なくとも 1 つの主応力が、破壊表面の引張である場合に発生すると仮定します。解析では、破損した弾性を使用して、亀裂の入ったコンクリートをモデル化します。亀裂に関連する永久歪みがないものとして仮定します。
引張軟化に関連するメッシュの感度を打ち消すために、解析では破壊エネルギー(単位面積当たり)、G f が材料特性であると想定します。特定の破壊エネルギー(単位体積当たり)、 g f は次に基づいたうえで G f に関連します。
|
|
l* は文字の長さまたは統合点の亀裂の幅です(参考 6)。
せん断保持係数 b は、ユーザによって指定されます。1 の値は、せん断力を失うことなく移動できるでこぼことした亀裂を意味します。0 の値は、せん断力を移動できない非常に滑らかな亀裂を示します。亀裂に関連するポワソンの効果(外側への延長)は無視されます。亀裂が閉じると、圧縮の圧力を完全に移動できます。
開いた亀裂に関連する圧力の要素は、同じ統合点のさらなる亀裂を検出するための破損曲面の定義に含まれていません。
破壊包絡線の計算
上記で示された通り (方程式 2、ρ=0)、a 3 は、等三軸の状態から指定されます。他の破損曲面パラメータ(a 1 、a 2 、およびc 0 )は、3 つの独立した圧力状態の非線型方程式(方程式 2、3、および 4)から解決します。他の実験の組合せについては、ユーザは計算してパラメータを直接入力する必要があります。
効果パラメータの場合(a
4
および k
0
)、解析は不均一な加工硬化を追加の効果項目によって支配されるものとして仮定します(方程式 5)。 つまり、プラスチックの有効歪み(![]() )の硬化と水圧(ζ)の依存性は分離可能であると想定されます。プラスチックの有効歪み(
)の硬化と水圧(ζ)の依存性は分離可能であると想定されます。プラスチックの有効歪み(![]() )は、硬化パラメータ k にのみ影響を与えます、そのため、ユーザは一軸圧縮実験に基づいて a
4
および k (
)は、硬化パラメータ k にのみ影響を与えます、そのため、ユーザは一軸圧縮実験に基づいて a
4
および k (![]() )を測定します。
)を測定します。
参考資料
- Chen, W.F. and Han, D.J., Plasticity for structural engineers, Springer, 1998
- Willam, K. and Warnke, E., Constitutive model for triaxial behavior of concrete. International Association for Bridge and Structural Engineering, Zurich, pp.1-30, 1975
- Kupfer, H. and Gerstle, K., Behavior of concrete under biaxial stresses, Journal of Engineering Mechanics, v99, n4, pp 853-866, 1973
- Imran I. and Pantazopoulou S., Plasticity model for concrete under triaxial compression. Journal of Engineering Mechanics, v127, n3, pp. 281-290, 2001
- Kang, H. and Willam, K., Localization characteristics of triaxial concrete model, Journal of Engineering Mechanics, v125, n8, pp941-950, 1999
- Crisfield, M.A., Non-linear finite element analysis of solids and structures, Vol. 2: Advanced topics, J. Wiley & Sons, New York, 1997
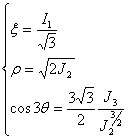 (1)
(1) 
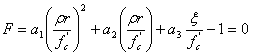 (2)
(2) 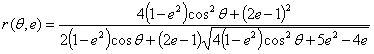 (3)
(3) 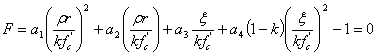 (5)
(5)