要約
通常、ソリッド モデルの有限要素解析(FEA)の精度は、幾何学的に高品質な要素で構成されるメッシュによって確保されます。Autodesk Simulation では、NASTRAN プロセッサによって使用される厳重なジオメトリ チェックを強制する自動ソリッド メッシュ化方法が開発されています。このソリッド要素の自動生成により、小さな間隔の空間を含んだメッシュが可能になります。 通常、こうした空間は、CAD ソリッド モデルなど、複雑な形状を持つパーツを考慮する場合にしか発生しません。この文書では、このような空間を含むメッシュから得られる結果について説明します。自動メッシュ化方法は空間のサイズを最小化するよう最適化されているため、その空間には微細孔という用語が使用されます。得られた結果は、完全に塗つぶされたパーツを使用して得られる結果、および解析的な解法と比較されます。ここでは、微細孔を含むモデルと完全に塗つぶされたメッシュを含むモデルで大きな違いのない結果が生じることを実証します。
はじめに
3D ソリッド モデルに FEA を適用する場合、4 面体の要素のみで構成されるメッシュ、またはブリック、ウェッジ、ピラミッド、4 面体のハイブリッド組み合わせのみで構成されるメッシュを生成する必要があります。後者のアプローチは、4 辺形で表現されているサーフェスのソリッドを考慮する場合に適しており、ピラミッドの生成を防ぐためにさらにリファインすることができます。正常なメッシュの生成では、NASTRAN のようなコードに対する最高品質の要素が構築されます。通常、自動メッシュ ジェネレータでは、低い縦横比を持つ要素が生成されます。Autodesk Simulation の自動ソリッド メッシュ ジェネレータでは、縦横比が最小化されるだけでなく、NASTRAN プロセッサによって使用されるジオメトリ チェックに適合した要素が構築されます。こうしたジオメトリ チェックには、アスペクト比、つぶれ度、テーパー比、内部角度、傾角度、ねじれ角、ねじれ係数が含まれます。
前述したような高品質の条件に適合する要素のみで構成されるメッシュでソリッドを完全に塗つぶすことが望ましいといえます。本来ならば、このようなメッシュでは高精度な FEA の結果が得られると期待できます。 しかし、問題は複雑なジオメトリのモデルではこうしたメッシュを得ることが常に可能ではないことです。その主な原因は、メッシュ ジェネレータが詳細な幾何学的フィーチャによって拘束され、要素の小さなサイズと大きなサイズ間における緩やかな遷移を含むメッシュの作成ができないためです。CAD の出現により、詳細なフィーチャを含むモデルが一般的になりました。フィーチャのサイズがメッシュ サイズと同等またはそれより小さい場合、遷移の必要がないため、完全に塗つぶされたパーツ全体に高品質の拘束を強制できます。ただし、このアプローチでは極度に小さなメッシュ サイズが必要とされます。その結果、非実用的な要素数を含むモデルが作成され、その解法には不適切な量の計算資源が必要となります。最終的なエンジニアの目標は実用的なアプローチを維持しながら最大限の精度を得ることにあります。
塗つぶされたソリッドによる拘束および要素の高品質の拘束を満たすために極度に微細なメッシュを作成するという非実用的な要件を回避するため、ソリッド内の重要ではないサイズの空間をそのまま残す自動メッシュ化方法が開発されています。このスキーマの主な目的は、厳重な幾何学的品質に準拠する要素のみで構築することで、できる限り高い精度を提供することです。それとは別にもうひとつの自動メッシュ化方法も開発されています。この方法では、結果として微細孔が生成される高品質なメッシュ化方法を最初に適用することでパーツを完全に塗つぶし、次にジオメトリ チェックに必ずしも適合する必要のない要素で小さな空間を塗つぶします。後述しますが、微細孔を含むメッシュ、およびジオメトリ チェックに違反するいくつかの要素を含む完全メッシュ共に大きな精度の損失はありません。後者のタイプのメッシュは、自動的に生成された一般的な FEA メッシュの向上として捉えることができます。こうしたメッシュには、低品質の要素が数多く含まれており、それが全体積の大部分を占めます。
前述のメッシュ化方法の両方では、サーフェスから内部に向けてマーチング アルゴリズムを使用して要素を構築することでこの問題に対応しています。このアプローチでは、サーフェス付近では厳重なジオメトリ チェックに適合する要素が生成され、パーツ内部深くのみに微細孔または低品質の要素が生成されます。精度を確保するという目的においては、FEA 解法で最も大きな勾配が通常発生するサーフェス付近に最高品質の要素を含むことが望ましいといえます。応力解析を含むほとんどの FEA アプリケーションでは、荷重および拘束、パーツとパーツの相互関係は通常サーフェス上で発生するからです。
この文書では、微細孔の存在によって、完全に塗つぶされたメッシュの同等モデルよりも明らかにより正確な FEA 結果を生成できることについて説明します。結果は、応力、熱、静電気を含む Lagrangian 定式化に基づいた解析タイプに対して得られたものです。微細孔を含むモデルは、流体解析などの Eulerian 定式化には適していません。
比較研究
FEA 解法での微細孔の効果は、微細孔を含むモデルと含まないモデルの結果を比較することで研究できます。具体的には、2 つの異なるメッシュ化方法を使用して取得したソリッド メッシュを持つ同一のサーフェス メッシュの結果を比較します。メッシュ タイプではなく、微細孔の効果に注目するために、Autodesk Simulation のハイブリッド ソリッド メッシュ タイプを使用したメッシュのみを考慮します。4 面体またはハイブリッドのソリッド メッシュ タイプいずれにおいても、存在する小さな空間を塗つぶすための 4 面体の要素を構築できない場合は、微細孔が発生します。両方のメッシュ化方法では、4 面体の要素は最終的にメッシュ段階でのみ生成されます。この研究で考慮しているモデルは、微細孔の発生につながるような小さなフィーチャを含まない、比較的なシンプルなジオメトリに見えるかもしれません。 しかし、ローカライズされたメッシュ リファインの結果として、急激な遷移がサーフェス メッシュ サイズに発生し、微細孔の生成が必要になっています。この文書で示すすべてのモデルには、効果を最大化するために典型的サイズから大きなサイズまでの微細孔体積分率が含まれていることに注意してください。
図 1 は、3 つのパーツで構成される CAD アセンブリのサーフェス ジオメトリを示しています。このサーフェスメッシュは、比較的大きな 0.00207 微細孔体積分率という結果になっています。このモデルおよびその比較対象である完全に塗つぶされたモデルに対して、線形材料による静解析および固有値解析が実行されています。図 2 は、両方のモデルでどのようにして相似する応力結果が得られたかを示しています。最初の 5 つの固有周波数を取得するためにモーダル解析が使用されており、表 1 では、両方のモデルでは解法でエンジニア上の大きな相違がないことが再び示されています。
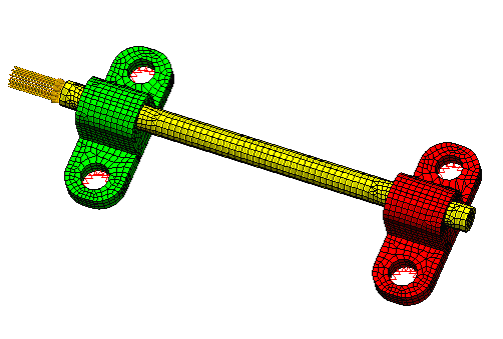
図 1: 2 つのブラケットに接続された円形の棒の 3 パーツアセンブリの FEA モデル(メッシュを含む)。ブラケットは、境界条件を使用して、フラットの終端(下側にある赤い 3 角形)にある穴のエッジに固定されています。線形材料による静解析では、棒の一方の終端に 5.0 x 108 ダインのサーフェス荷重が適用されています。
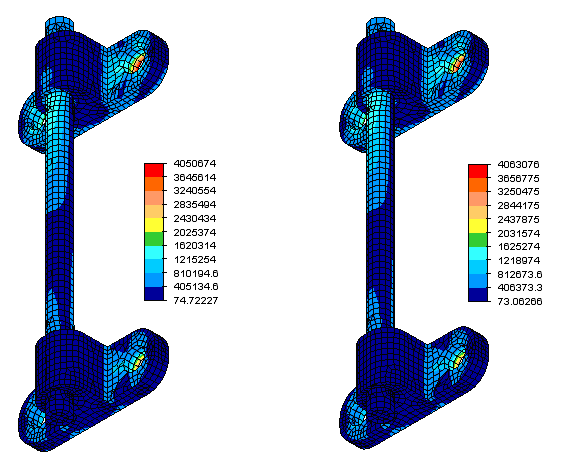
図 2: 2 つのブラケットに接続された円形の棒の 3 パーツアセンブリの線形材料による静解析から得られたミーゼス応力の分布。左側の図は微細孔のないモデルを示し、右側の図は微細孔を含むモデルを示しています。後者では、前者よりも 0.31% 大きい最大応力が予測されています。
|
モード番号、n |
微細孔を含まないモデル |
微細孔を含むモデル |
比率の相違(%) |
|
1 |
1132.8 Hz |
1129.2 Hz |
0.318 |
|
2 |
1169.9 Hz |
1168.1 Hz |
0.154 |
|
3 |
1228.1 Hz |
1226.1 Hz |
0.163 |
|
4 |
2877.4 Hz |
2875.0 Hz |
0.083 |
|
5 |
3007.0 Hz |
3003.2 Hz |
0.126 |
|
表 1: 2 つのブラケットに接続された円形の棒の 3 パーツアセンブリの固有値解析から得られたモーダル周波数。これらすべての周波数を比較するとその違いが 0.32% 以内であることに注意してください。 |
|||
図 3 は、微細孔を含む/含まないリングの単一パーツモデルの定常熱伝導解析の結果を示しています。微細孔は、より典型的な 0.00046 体積分率という結果になっています。線形材料による静解析の場合と同様、両方のバージョンのモデルでは非常に相似する結果が生じています。図 4 は、2 つのバージョンのリング モデルに Autodesk Simulation の メカニカル イベント シミュレーション(MES)を使用して得られた変位結果を示しています。非線形 FEA でも、微細孔の存在が結果に大きな影響を及ぼしていません。最後に図 5 は、2 つのバージョンのリング モデルに Autodesk Simulation の静電電流と電圧解析を使用して得られた電圧結果を示しています。 静電気と熱解析間の基準となる相似点から予想できるとおり、微細孔の存在は結果に対してごくわずかな影響しか及ぼしていません。
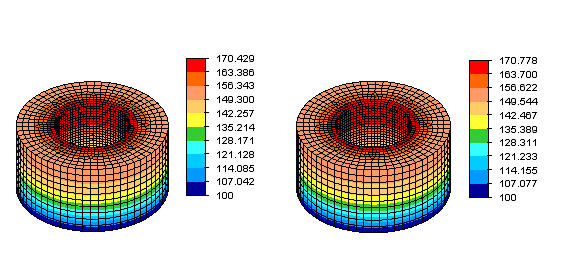
図 3: 基礎が 100 °F に維持され、内面に 0.642 BTU/(sec in2)の熱流束が適用されたリング モデルに対する定常熱伝導解析から得られた温度分布。左側の図は微細孔のないモデルを示し、右側の図は微細孔を含むモデルを示しています。後者では、前者よりも華氏 0.349 度高い最大温度が予測されています。
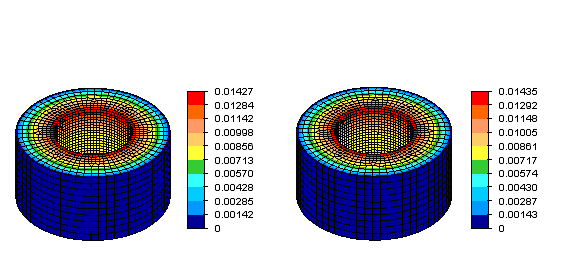
図 4: 固定された外面を持ち、内面に最大 100 lb/in2 秒に達する時間比例の圧力が適用されたリング モデルに対するメカニカル イベント シミュレーション(MES)から得られた変位の大きさの分布。結果は、0.1 秒イベントの終わりです。左側の図は微細孔のないモデルを示し、右側の図は微細孔を含むモデルを示しています。後者では、前者よりも 0.56% 大きい最大節点変位が予測されています。
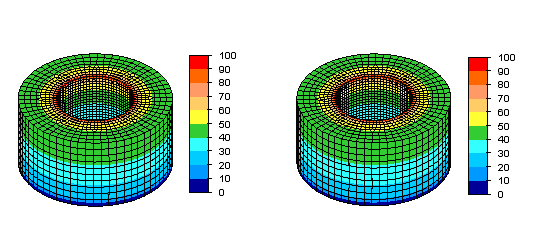
図 5: 上面の内部エッジに 100V の電圧、および外面の外側エッジに 0 V の電圧が適用されたリングモデルに対する静電電流と電圧解析から得られた電圧分布。左側の図は微細孔のないモデルを示し、右側の図は微細孔を含むモデルを示しています。外側上部のエッジの最大電圧の比較では、2 つのモデルに 0.02% の違いがあることが示されています。
結論
精度に重点を置いた新しい自動メッシュ化方法が開発されています。この方法では、微細孔をそのまま残しながら、高い幾何学的品質の要素だけが生成されます。 このメッシュ化方法はさらに拡張され、高い幾何学的品質の拘束を満たさない要素を含む小さな空間を塗つぶすことが可能になっています。これら両方の方法では、高精度の FEA 結果が生成可能なメッシュを生成することができます。典型的な体積分率から大きな体積分率の微細孔を含む FEA モデルと完全に塗つぶされたメッシュのモデルでは、同等のエンジニア精度結果を生成することがいくつかの例で実証されました。