有限要素解析(FEA)は、形式が異なっていても、その本質的な目的は数式の集合を解決することです。次に示す 2 つの シンプルなバネ モデルを参照してください。F1 および F2 は適用荷重、K1 および K2 はバネの剛性、X1 および X2 は、各終端のたわみです。適用荷重のいずれかがゼロになり得ますが、それぞれは既知の値です。延長によって各バネに生じる力は既知ではありませんが、F = k*x の直接法の定式化から計算することができます。バネ 1 で X1 の量の延長、バネ 2 で(X2-X1)の量の延長が発生すると考慮すると、各節点力の合計を計算する数式を次のように作成できます。
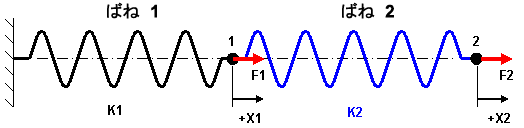
| F1 - K1*X1 + K2*(X2-X1) = 0 | 節点 1 |
| F2 - K2*(X2-X1) = 0 | 節点 2 |
数式を構成しなおすと次のようになります。
| F1 = (K1 + K2)*X1 - K2*X2 | 節点 1 |
| F2 = -K2*X1 + K2*X2 | 節点 2 |
これらの数式は、次のようにマトリックス形式で表現できます。
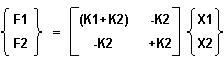
または、簡潔な表記として、{F} = [K]{X} で表すことができます。
FEA では、数式マトリックスの解決方法は、ソルバーによって決定されます。コンピュータ ハードウェアや計算手法が進化すると、新たなソルバーがソフトウェアに追加されます。各解析タイプでは、さまざまなソルバーを選択することができます。ほとんどの場合、既定のオプションは[自動]です。この場合、解析に最適なソルバー(通常、モデルのサイズ(数式の数)に基づいて)がソフトウェアによって選択されます。次に、各ソルバー タイプの一般的な方法論について説明します。
要素がどのように接続されているかによって異なりますが、剛性マトリックス[K]は、通常、密度が非常に低くなります。エントリの多くはゼロです。ゼロの値は、解法に対して何も貢献しないため、ほとんど解法では何らかの形でゼロの項を無視するようにプログラム化されています。少ない量のメモリを使用してマトリックスを保管する一方で最小限のメモリ量を実現するために最適化が必要な方法もあれば、マトリックスの保管により多くの変数を使用する(より多くのメモリが必要)一方で全体的に高速な方法もあります。
次に、数式の集合の解法によって、解析に必要な時間が決定します。モデルが適切に設定されている場合に(静的応力モデルが適切に拘束され、定常熱伝導に熱源と熱削除方法が設定されているなど)、必ず解法が提供される直接法があります。ガウスの消去法や行列反転などの手法は、直接法の一例です。解法が想定される間接法もあります。方程式系に想定の解法を代用することで、未知のそれぞれに対して、より優れた予測を取得します。この処理は、解法の変更がなくなるまで繰り返されます。したがって、この手法は、反復法と呼ばれます。
最後に、剛性マトリックスは、通常 FEA では対称的であるという点です。これらの例の場合では、斜め線上またはその上にある項のみを保管する必要があります。そのため、マトリックスの解決におけるメモリ要件および操作数を削減できます。マトリックスを非対処に変更する効果が含まれる場合(熱伝達解析における物体間輻射、メカニカル イベント シミュレーションでのアクチュエータ要素など)、マトリックス全体を保管および処理する必要があります。この解法は、それに当てはまりません。
利用可能な一般的なソルバーを次に示します。それぞれのソルバーには、特定の解析タイプに応じたバリエーションがあります。例えば、モード解析には、反復ソルバー(サブスペース)がありますが、これは、線形静的応力で利用可能な反復ソルバー(AMG、または Algebraic MultiGrid)のバリエーションです。解析に使用するソルバーのタイプは、[設定]
[モデル設定][パラメータ]から設定できます(または、ツリー表示で[解析タイプ]エントリを右クリックして、[解析パラメータを編集]を選択します)。
スパース ソルバー
- マトリックスに対する直接法を提供します。
- ハンド幅は最適化されません。そのため、その処理に要する時間を節約できます。
- マトリックス全体は保管されず、非ゼロの項のみが保管されます。(これが、スパース ソルバーの用語の由来です。)
- 保管される剛性マトリックスからの項の数量はより少ないですが、非ゼロ項の位置を保管する必要があるため、より多くの変数を必要とします。その結果、スパース ソルバーは、その他 2 つのソルバーに比べ、より多くのメモリを必要とします。
- スパース ソルバーは、中規模サイズのモデルにおいて最も高速なソルバーです。
反復ソルバー
- マトリックスに対する間接法を提供します。したがって、ユーザは実行する反復の最大数、および解法の収束完了を決定する収束基準を指定する必要があります。指定した反復数でマトリックスに対する解法が検出されるかどうかは保証されません。
- 反復ソルバーは最初の予測から開始する必要があるため、プロセッサによっては前提条件が設けられています。そのため、モデルを効率的に解決するためのより多くのオプションが提供されます。
- ハンド幅は最適化されません。そのため、その処理に要する時間を節約できます。
- 反復ソルバーでは、スパース ソルバーに比べ、より少ないメモリを必要とします。
- 収束可能時には、スパース ソルバーは大規模サイズのモデルにおいて最も高速なソルバーです。 モデルの規模は、解析タイプに依存します。 線形静的応力解析では、150,000 の数式(自由度)で大規模と考慮されます。流体解析では、50000 の数式で大規模と考慮されます。 重要: 解法の精度は収束許容誤差に依存します。許容誤差が小さいほど解法の精度が向上しますが、より多くの反復が必要になります。反復解の場合と同様、結果を確認して、適切な精度に合致していることを確認する必要があります。場合によっては、精度を確認する最良の方法として、異なる収束許容範囲を使用して解析を 2 回実行することができます。注: マトリックスを解決する反復プロセスは、収束の 1 つの必要レベルとして捉えることができます。その結果、数式の集合の解法が提供されます。解析が非線形でない場合、物理的解法を収束するために問題の解決を繰り返す必要があります。例えば、輻射では、数式の解決が非線形になります。非線形の数式に対する解法を検出するために、複数の反復が必要になります。(通常、数式は線形であるため、1 つの解法しか必要ありません。)モデルを解決するための反復プロセスと、方程式系を解決するための反復プロセスを混同しないでください。ヒント: 解析で、反復ソルバーでの収束に失敗し、 マトリックスが正定値行列ではない可能性または事前条件システムの条件 = でない可能性があるというメッセージが表示された場合、問題の原因が静的に不安定なモデルである場合があります。静的応力解析では、すべてのコンポーネントが静的に安定していることを確認してください。モデルに接触が含まれる場合は、「解析の設定と実行」>「解析を実行する」>「線形解析を実行する」>「ギャップ要素による解析を実行する」も参照してください。