ビーム プリロードによって、ビーム要素の長さ全体にわたって軸荷重が適用されます。締結パーツや鋼索など、モデルまたはパーツ内部の荷重(節点力などの外部の荷重とは別)をシミュレーションする場合に使用します。解析全体にわたって一定である外部の荷重とは違い、他の構造部分が無限に剛性を有する場合、予荷重の大きさは要素内における値となります。ただし、構造物の剛性は無限大ではないため、予荷重については、構造物が変形し予荷重の一部が軽減されたという結果が得られます。実際の作業では以下の点に注意してください。
予荷重を適用する
線形解析では、ビーム プリロードを利用できるのは静的応力のみです。[固有値解析(初期応力考慮)]、[線形座屈解析]では利用できません。
非線形解析では、MES および非線形材料による静解析でビーム プリロードを利用できます。非線形材料による固有値解析でもビーム プリロードを適用することができます。ただし、この解析タイプの場合、応力硬化の効果が考慮されないため、ビーム プリロードは解析結果に反映されません。MES Riks 解析では、ビーム プリロードを利用できません。
- [要素タイプ]を定義し、パーツを[ビーム]要素にします。
- [選択]
 [選択]
[選択] [ライン]コマンドで、ビーム要素を選択します。
[ライン]コマンドで、ビーム要素を選択します。 - 表示領域で右クリックし、[追加]プルダウン メニューから[ビーム プリロード]コマンドを選択し、各ビーム要素に予荷重を追加します。
- [軸力]フィールドに予荷重の大きさを入力します。正の値を入力すると、要素が初期に引張状態になるため、解析によってビームの端がともに表示されます。負の値を入力すると、要素が初期に圧縮状態になるため、解析によってビームの端が分離されます。
- 予荷重のあるビーム要素は、ライン セグメント上に記号 B を有します。予荷重を調整するには、ツリー表示内の[FEA オブジェクトグループ]の予荷重エントリを選択するか、ライン選択モード([選択]
 [選択]
[選択] [ライン])で表示領域内の記号 B を選択します。
[ライン])で表示領域内の記号 B を選択します。
- コンテキスト メニューのコマンドを選択する方法のほかに、リボンの[セットアップ]タブの[梁荷重]パネル内にある[ビーム プリロード]コマンドをクリックする方法もあります。
- 初期ひずみは 0 として認識されます。したがって、予ひずみを考慮しないと、計算されたひずみが計算された応力と矛盾するように見えます。
- 線形解析の場合、予荷重は解析のすべての荷重ケースに適用されます。荷重乗数の影響は一切受けません。
- 非線形解析の塑性材料モデルでは、予ひずみが計算されるため、その効果がひずみ結果に反映されます。
実際の作業時の注意点
上述したとおり、ビーム要素に適用された部材が荷重に反応して圧縮するため、予荷重の一部は解析では緩和されます。トルク レンチで締められるボルト内の予荷重など、適用した予荷重が最終的な荷重となる場合は、適用されたビーム プリロードはパーツの圧縮を補うために増加させる必要があります。部材の剛性と最終的な荷重がわかっている場合、ビーム要素に適用する初期の予荷重の計算方法は次のとおりです。
|
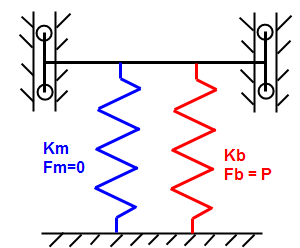
伸張して大きさ P の予荷重を生じ、部材(青のばね K m )に接触するビーム(赤のばね K b )の場合を見ていきます。このビームと部材の圧縮量は Δ です。ビームは伸張してから接触して部材を圧縮するため、ビームの最終的な荷重 F' は、圧縮の倍の剛性を除いた予荷重と等しくなり、部材の同じ荷重(符号は逆)は圧縮の倍の剛性と等しくなります。したがって、2 つの方程式と 2 つの未知数(Δ)があります。 |
|
ビームの最終的な荷重 F' = P - K b Δ |
|
部材の最終的な荷重 F' = K m Δ |
この 2 つの方程式を解くと、最終的な荷重 F' は次のようになります。
F' = P[K m /(K m +K b )]
K b はビームの剛性、K m は部材の剛性、P はビームに適用された予荷重です。
ボルト締結に関しては、ボルトの圧力分布の条件によって、部材の剛性を計算する方程式が数多くあります。その一例を次に示します。この例では圧力分布の頂角は 30 度、座金の直径はボルト直径の 1.5 倍となっています。
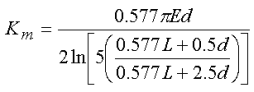
L はボルト締め部材の総厚、d はボルトと穴の直径となります(出典: Budynas, Richard G and Nisbett, J. Keith, Shigley's Mechanical Engineering Design, McGraw-Hill, Inc, Eighth Edition)。
このトピックの重要な項目は P/F' 率です。多くの場合、既知の予荷重はボルトと部材(F')における最終的な荷重となるので、上記の方程式を使用して予荷重 P を計算し、ビーム要素に適用することができます。結果の例を次の表に示します。たとえば L/d が 2 の場合、ビーム要素に適用する予荷重はボルトと部材の最終的な予荷重の 1.35 倍となります。設計はそれぞれに異なるため、K m に関する上記の方程式と表は代表例にすぎません。
|
長さ/ボルト直径 L/d |
予荷重/最終的な荷重 P/F' |
| 0.50 | 1.60 |
| 1.00 | 1.48 |
| 2.00 | 1.35 |
| 3.00 | 1.28 |
| 4.00 | 1.23 |
| 6.00 | 1.17 |
| 10.0 | 1.12 |
注:
- 部材が複数の材料で構成されている場合は、剛性は直列のばねとして計算できます。この場合、同様の剛性 K eqv は次のように導き出されます。
1/K eqv = 1/K 1 + 1/K 2 + 1/K 3 +
- ソフト ガスケットなど、ある材料が他の材料に比べて著しく強度が低い場合は、強度の低い材料が基準となり、K eqv ≈ K gasket となります。
- いくつかの重要なケースでは、予荷重を除き、モデルに荷重を一切適用せずに解析を実行し、最終的な荷重 F' を求めるために必要な予荷重 P を導かなければならない場合もあります。
同様の手法は、温度を使用して予荷重をモデルのパーツに適用する場合に利用できます。