Duncan-Chang 材料モデルは、土壌の解析に使用されます。このモデルは、双曲線の応力/ひずみ関係を仮定し、土壌の 3 軸試験に基づいて開発されたものです。オリジナルのモデル(Duncan and Chang、1970 年)は、一定のポアソン比を仮定していますが、修正モデルでは、ポアソン比の変動にも対応されており、応力依存のポアソン比(E-v モデル、Kulhawy and Duncan、1972 年)や応力依存の体積弾性率(E-B モデル、Duncan et al.、1980 年)のモデルがあります。
定式化
モデルでは、標準的な土壌の 3 軸試験に基づき、次の双曲関係によって応力/ひずみを近似します。
|
|
ここで、σ 1 および σ 3 は最大および最小の主応力、ε 1 は最大の主ひずみ(軸ひずみ)です。 注意が必要なことは、ここでは土壌力学の記号表記方法に従って記述されているため、連続体力学とは逆の表記になるという点です。定数 a および b は、試験データによって校正されるもので、次のように記述できます。
|
|
ここで、E i は初期正接係数、(σ 1 -σ 3 ) ult は双曲線の漸近値であり、次のように崩壊率によって土壌強度に関連付けられます。
|
(σ 1 -σ 3 ) f = R f (σ 1 -σ 3 ) ult (3) |
崩壊率 R f は、常に 1 未満であるのは明らかであり、 0.75~1 と求められています(Duncan and Chang、1970 年)。
Duncan-Chang モデルでは、初期正接係数を次のように定義しています。
|
|
ここで、弾性率数値 K および弾性率指数 n は無次元の材料パラメータ、p a は単位系選択の影響を除去するために定式化で使用される大気圧です。
土壌の崩壊は、次に示すモール クローン(Mohr-Coulomb)の崩壊基準によって規定されます。
|
|
ここで、c および φ はモール クローン強度パラメータです。非粘性度の場合、モール包絡線は通常、曲線となり、その偏差は次の形式で表されます。
|
|
ここで、φ 0 は封圧 σ 3 の単位大気圧における摩擦角、Δφ 0 は φ の減少(σ 3 の 10 倍増加時)です。
増分形では、正接係数を次のように表すことができます。
|
E t =(1-R f S) 2 E i (7) |
ここで、S は応力レベル、すなわち増加した強度の割合です。
|
|
ここで、(σ 1 -σ 3 ) は自身の履歴最大値未満となり、土壌は除荷または再荷重状態で、正接係数は次のように定義されると仮定します。
|
|
ここで、K ur は除荷/再荷重係数であり、常に主荷重係数 K より大きくなります。除荷/再荷重係数の指数は、主荷重の場合と同じです。
同様に、E-v モデル(Kulhawy and Duncan、1972 年)においても、初期ポアソン比は次のように表すことができます。
|
|
また、正接ポアソン比は、次のように表されます。
|
|
ここで
|
|
および D、F、G は材料パラメータです。
E-B モデル(Duncan et al.、1980 年)においては、体積弾性率は次のように表されます。
|
|
ここで、K b および m は、それぞれ体積弾性率の数値と指数です。
初期応力
通常、土壌体の初期応力状態を考慮することは重要です。 現在、ソフトウェアでは、均一な双曲線圧力と自重から与えられる初期圧力状態の 2 タイプが提供されています。これらの初期応力は、静的平衡状態であると仮定されるため、解析における応力やひずみの値には寄与しません。解析における応力やひずみの値は、外部から加えられた荷重によって生じます。すなわち、[結果]環境に示された応力結果が初期応力によって変化することはありません。また、初期応力が初期変位を生じることもありません。この仮定が適切でない場合には、荷重履歴を明示的にシミュレートしてください。
安定化
標準の 3 軸圧縮試験中、封圧 (σ 3 ) は常に 0 より大きくなりますが、一般的な有限要素解析では、0 以下になる可能性があります。数値的に安定した解析を得るには、このケースに対して一連の弾性率を用いる必要があります。ユーザは、値(ヤング率と静止状態のポアソン比)を材料特性の[高度]タブで指定することができます。これらが指定されない場合、 既定値の E 0 =0.01K*p a および ν 0 =0.499 が使用されます。
崩壊(応力レベルが 1 に達した)後、土壌は、実質的にその荷重吸収力を失います。安定した解析には、一連の残留係数が必要になります。ユーザは、値(ヤング率と崩壊時のポアソン比)を[高度]タブに指定することができます。こららが指定されない場合、既定値の E 1 =0.001K*p a および ν 1 =0.499 が使用されます。これらの値は、崩壊前の弾性率の下限値としても使用されます。
シミュレーション結果は、上述の安定化係数によって大きく影響される場合があります。 静止状態の弾性率を実験的に求めることは可能ですが、通常、Duncan-Chang モデルの適切な崩壊係数を求めるのは困難です。 ただし、Duncan-Chang モデルは、崩壊前の解析に使用することが意図されたものであり、崩壊が限定的な場合やローカル的な場合にはまずまずの結果が得られる可能性がある点に注目する必要があります。
制限事項
Duncan-Chang モデルは、多くの現実問題の解析に有効であり、標準の 3 軸圧縮試験による設定も単純です。3 軸試験の結果が利用できない場合は、モデル パラメータも参考文献から豊富に利用できます。ただし、ユーザは重要な制限事項を認識する必要があります(Duncan et al.、1980 年)。
- 中間主応力 σ 2 は解析されません。
- 大規模な崩壊が発生した場合、結果が信頼できないことがあります。
- せん断応力(せん断ダイラタンシー)の変化による体積変化は考慮されません。
- 入力パラメータは基本的な土壌プロパティですが、限定された範囲の条件に対する経験値にすぎません。
- モデルは、主として、準静的解析を意図しています。
リファレンス
- Duncan, J. M. and Chang, C. Y., Nonlinear analysis of stress and strain in soils, Journal of the Soil Mechanics and Foundations Division, ASCE, 96(SM5), 1629-1653, 1970.
- Kulhawy, F. H. and Duncan, J. M., Stresses and movements in Oroville Dam, Journal of the Soil Mechanics and Foundations Division, ASCE, 98(SM7), 653-655, 1972.
- 3. Duncan, J. M., Byrne, P., Wong, K. S. and Mabry, P., Strength, stress-strain and bulk modulus parameters for finite element analysis of stresses and movements in soil masses, Report No. UCB/GT/80-01, Dept. Civil Engineering, U.C. Berkeley, 1980.
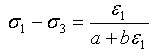 (1)
(1)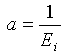 (2)
(2)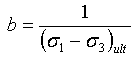
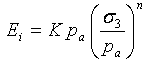 (4)
(4)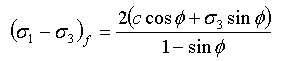 (5)
(5)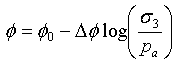 (6)
(6)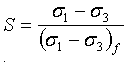 (8)
(8)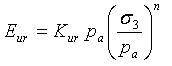 (9)
(9)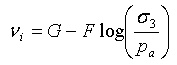 (10)
(10)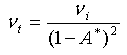 (11)
(11)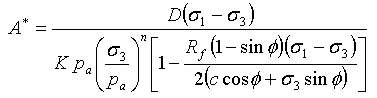 (12)
(12)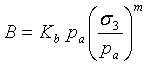 (13)
(13)