Wybór krzywej

Podczas używania graphera wejściowego w celu zdefiniowania wartości zmieniających się podczas symulacji dostępne są różne opcje pozwalające zdefiniować sektory krzywej . Opcje zdefiniowane są w formie praw lub funkcji matematycznych tworzących określone typy krzywych.

Uwaga: Gdy dane wyjściowe są używane we wzorach zdefiniowanych przez użytkownika, do ich nazw wyświetlanych w przeglądarce dodawane są nazwy właścicieli zamknięte w nawiasy. Na przykład: „Siła (Obrót:7)”

Wybór funkcji matematycznych i definiowanie ich parametrów

Definiowanie sektorów krzywych polega na przypisywaniu im funkcji matematycznych (praw). Można utworzyć kilka kolejnych sektorów i każdemu przypisać własne prawa lub zestawy różnych praw, np.: funkcja sin oraz funkcja ramp. Można na przykład utworzyć sektor z rampą sześcienną i kolejny sektor z sinusem. Oprogramowanie narzuca stosowanie ciągłości praw globalnych. Może to być przyczyną pomylenia pierwszego punktu drugiego sektora z ostatnim punktem pierwszego sektora i spowodować automatyczne przesunięcie innych punktów. Często, aby otrzymać żądaną krzywą, należy dodać dodatkowe funkcje.

Po wybraniu prawa i przesunięciu go do pola Listy praw sektora należy dodać odpowiednie parametry prawa. Aby dodać parametry, wykonaj następujące czynności:

Po wybraniu sektora krzywej i dodaniu warunków, które zostaną zastosowane, można rozpocząć definiowanie wybranego sektora krzywej.

Na Liście dostępnych pól praw kliknij strzałkę skierowaną w dół i wybierz prawo, które chcesz użyć.
Kliknij przycisk , aby zastąpić prawo w wybranym sektorze prawem wybranym z listy.
Możesz dowolnie zastępować i wybierać prawa, ale nowe prawa nadpisują prawa wyświetlane w polu Lista praw sektora.

Do jednego sektora można wstawić wiele praw. Aby dodać kolejne prawa do danego sektora, powtórz pierwszą z opisanych czynności, ale kliknij przycisk . Aby usunąć prawo z sektora zawierającego wiele praw, wybierz zbędne prawo w polu Lista praw sektora i kliknij przycisk .

Wprowadź wymagane właściwości prawa wyświetlanego w polu Lista praw sektora.

Po wyświetleniu

Wprowadź właściwości

Rampa liniowa, Rampa sześcienna, Cykloida, Harmoniczny, Zmodyfikowany sinus, Zmodyfikowany trapez

Współrzędne (X1, Y1) i (X2, Y2) punktów definiujących krzywą i/lub wprowadź wartości Nachylenia, aby ustawić średni gradient linii. Krzywą można zdefiniować, wprowadzając współrzędne punktu początkowego i końcowego lub wprowadzając współrzędne punktu początkowego oraz średnie pochylenie sektora.

Krzywa jest symetryczna względem środka sektora.

Obszar pod krzywą jest równy trójkątowi pod odpowiednią rampą liniową.

Rampa liniowa ma stałe nachylenie - dwa punkty sektora są połączone linią prostą.

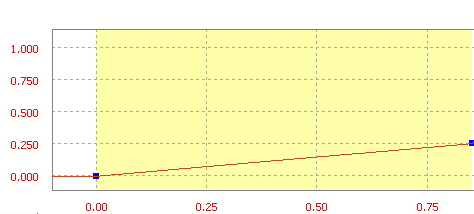
Rampa liniowa z nachyleniem 30 cali/sek.

Rampa sześcienna jest definiowana przez wielomian 3 stopnia.

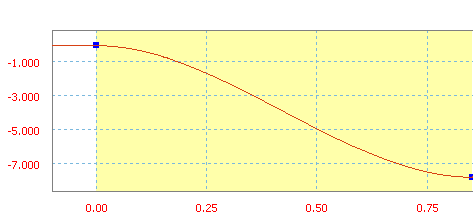
Rampa sześcienna ze średnim nachyleniem 70 cali/sek.

Cykloida jest funkcją rampy z sinusa/cosinusa.

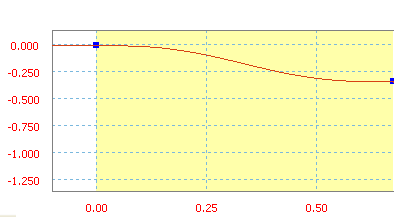
Rampa cykloidalna ze średnim nachyleniem -50 cali/sek.

Harmoniczna jest funkcją rampy z sinusa/cosinusa.

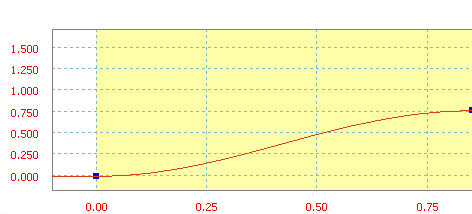
Rampa harmoniczna ze średnim nachyleniem 90 cali/sek.

Zmodyfikowany sinus jest funkcją rampy z sinusa/cosinusa.

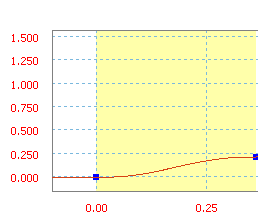
Rampa zmodyfikowany sinus ze średnim nachyleniem 60 cali/sek.

Zmodyfikowany trapez jest funkcją rampy z sinusa/cosinusa.

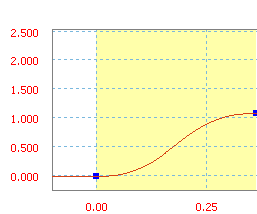
Rampa zmodyfikowany trapez ze średnim nachyleniem 300 cali/sek.

Po wyświetleniu	wprowadź
Sinus	wartość Amplituda pozwalająca określić wysokość krzywej od mediany cyklu, wartość Częstotliwość, aby określić liczbę cykli na jednostkę osi X i wartość Faza, aby określić odległość od początku cykli do początku sektora. Sinus jest funkcją klasyczną. Jednostki amplitudy są taki same jak kontrolowana zmienna (ruch wymuszony, siła). Jednostki częstotliwości są odwrotnością zmiennej użytej na osi X (w Hz, jeśli jest to czas). Faza jest wyrażona stopniami lub radianami.
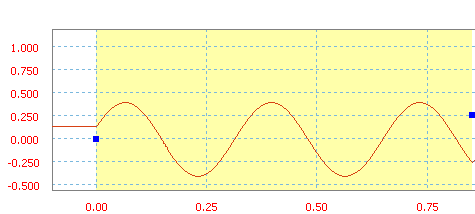
Funkcja sinus mająca amplitudę wynoszącą 40, częstotliwość 3 Hz oraz fazę 20 stopni.
Wielomian	Wielomian jest funkcją wielomianową i w tym wypadku ma do 5 stopni. Dostępne są dwie metody definiowania współczynników wielomianu. Metoda 1 - Określenie wartości współczynników Należy wprowadzić wartość a0 oraz tyle kolejnych wartości a, ile konieczne. Metoda 2 - Importowanie pliku tekstowego Przycisk pozwala otworzyć okno dialogowe Otwórz, które umożliwia import pliku definiującego wielomian. Opcja Stopień pozwala ustawić stopień wielomianu dla krzywej znajdującej się w wybranym sektorze. Przycisk pozwala obliczyć stałą wartość oraz wartości przy pierwszych pięciu stopniach tego wielomianu. Czynniki a0, a1, a2, a3, a4, a5 pozwalają wyświetlić stałą wartość oraz wartości przy pierwszych pięciu stopniach tego wielomianu. Jeśli zachodzi taka potrzeba, te wartości mogą być edytowane. Plik tekstowy powinien mieć następujący format: //komentarz - wiersze komentarza są opcjonalne oraz poprzedzone dwoma ukośnikami. xl yl - lista punktów określonych przez wartości x i y. ... - definicja jednego punktu dla każdego wiersza lub linii. xn yn - dowolna ilość punktów. Możesz wprowadzić odpowiednie wartości lub warunki zostaną wyliczone za pomocą interpolacji metodą najmniejszych kwadratów.
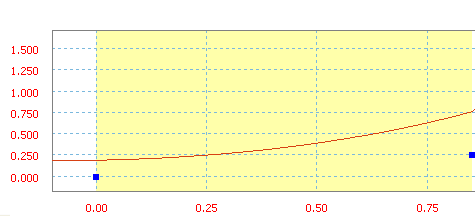
Wielomian o czynnikach a0=20 cali, a1=10 cali/s, a2=50 cali/s² i a3=20 cali/s³.
Splajn	Wartość Nachylenia, aby określić nachylenie linii. Splajn jest funkcją sześcienną, wykorzystywaną do interpolacji pomiędzy kolejnymi punktami. Splajny można definiować na wiele sposobów. Są to: Używając myszy, można szybko zdefiniować punkty wejściowe. W obszarze graphera kliknij dwukrotnie lub kliknij prawym przyciskiem i wybierz opcję Dodaj punkt. Jednak ten sektor traktowany jest to jako zestaw kolejnych sektorów, a nie pojedynczy sektor krzywej. Importując plik tekstowy można wprowadzić dokładniejsze współrzędne. Wartość Początkowe nachylenie określa nachylenie pierwszego punktu. Wartość Końcowe nachylenie określa nachylenie końcowego punktu. Można wczytać wcześniej zdefiniowany splajn.
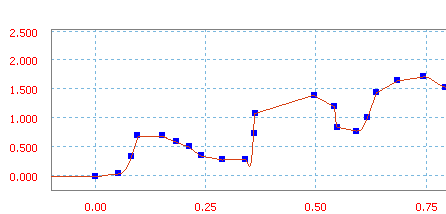
Splajn zdefiniowany poprzez dodawanie punktów.
Definiowany splajn można zapisać bez względu na sposób definiowania. Uwaga: Nie można dodać innych praw do sektora zdefiniowanego przez splajn. Jeśli prawo sektora zostanie zastąpione splajnem, to początkowe i końcowe nachylenia są automatycznie zbierane z poprzedniego i kolejnego sektora; można je jednak zmodyfikować później.
Aby używać pliku tekstowego zawierającego punkty styczności, należy zastosować następującą strukturę:
// komentarze	Można włączyć jeden lub więcej wierszy komentarza w pliku. Każdy wiersz musi rozpoczynać się znakami „//”. Wiersze komentarza są opcjonalne, ale są przydatne, ponieważ umożliwiają zanotowanie przeznaczenia splajnu.
[Styczność] T1 T2	Określ wartości stycznych dla punktu początkowego (T1) i punktu końcowego (T2) sektora. Te wartości są wyświetlane jako nachylenie „początkowe” i „końcowe” w interfejsie użytkownika. Jeśli nie podano żadnej wartości, przyjmowana jest wartość stycznej na poziomie 0,0 (styczna pozioma). Tak jak w przypadku wierszy komentarza, ten wiersz jest opcjonalny, ale, jak zaznaczono, gdy nie istnieje żadna wartość styczna, należy przyjąć pewne założenia.
X₁ Y₁ ... X_n Y_n	Lista współrzędnych punktu. Na liście można umieścić dowolną liczbę punktów. Określ jeden punkt w każdym wierszu.
Przykładowy plik tekstowy	// // Dane wejściowe symulacji - punkty splajnu // Wartość: Moment obrotowy połączenia (N mm) // Odniesienie: Czas s [Styczność] -3,40775 -5,27803 +0.000 +0.000 +4.313 +1.510 +7.954 -9.756 +1.000 +0.000
Wzór	wzór w polu wzoru, aby zdefiniować krzywą. Wzór to równanie zawierające funkcje i słowa kluczowe. Ta opcja jest dostępna tylko dla definicji połączenia i sił zewnętrznych. Nie można wymusić ruchu w stopniu swobody. Ciągłość z sąsiednimi sektorami nie jest zachowywana automatycznie. Należy je zdefiniować w taki sposób, aby uniknąć kolizji podczas symulacji. Wzory są ograniczone do 255 znaków. Można wybrać dowolne funkcje: abs fmod a cos cos log10 sqrt asin sinh log sqr atan sin pow trunk atan2 tanh sign pow10 floor cosh tan sign0 exp round
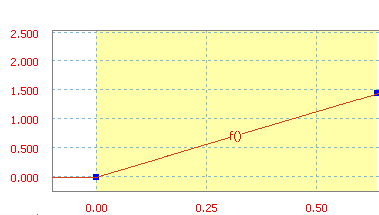
Krzywa opisana za pomocą wzoru: Y = X + 37,

Przykład 1

Utworzono 3 sektory. W drugiej sekcji utworzono sinusoidę o niskiej częstotliwości.

Widoczna jest krzywa przed i po utworzeniu sinusoidy. Trzeci sektor został przesunięty w pionie, aby zachować ciągłość między sektorami. Aby otrzymać żądaną krzywą, należy dodać dodatkowe funkcje.

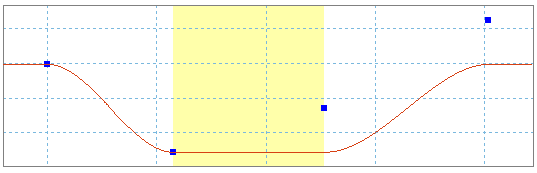
Przykład 2

Definicje niektórych funkcji są ograniczone. Aby otrzymać sinusoidę oscylującą wokół wartości 300, należy dodać stałe prawo o wartości 300 i prawo sinusoidy.

Uwaga: Kolejność dodawania praw nie jest istotna.

Zmiany niezerowego nachylenia można modelować, używając kombinacji rampy i sinusoidy.

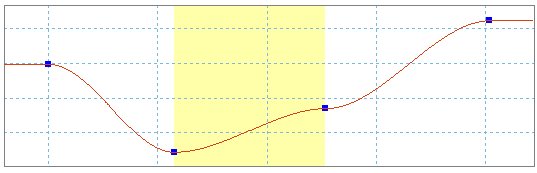
Przykład 3

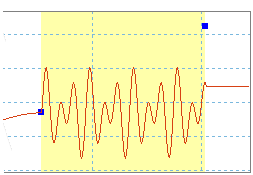
Aby symulować drgania w ruchu zmiennym, można połączyć prawa sinusoidy z częstotliwościami i amplitudami.

Definiowanie wartości poza sektorem krzywej

Interesujące jest zdefiniowanie zachowania zmiennej poza sektorami krzywej: przed pierwszym i po ostatnim. Po wybraniu obszaru poza krzywą i dodaniu warunków, które zostaną zastosowane, można rozpocząć definiowanie wybranego obszaru.

Wybierz definicję wybranego obszaru poza krzywą.
Jeśli wybrana została opcja Cyklicznie, kliknij przycisk Start.
Otwarte zostaje okno dialogowe Wybór punktu początkowego.
W oknie dialogowym Wybór punktu początkowego kliknij strzałkę skierowaną w dół (znajdującą się w prawej części pola).
Otwarte zostanie menu i wyświetlone zostaną wszystkie punkty rozpoczynające sektor krzywej.
Kliknij punkt rozpoczynający sektor krzywej, który chcesz przekopiować do tego obszaru.
Kliknij przycisk OK.

Obszar poza krzywą można zdefiniować na pięć sposobów. Są to:

Wartość stała	Ustawiana jest wartość stała równa pierwszej wartości krzywej, o ile definiowany jest obszar po lewej stronie pierwszego punktu lub ostatnia wartość krzywej, o ile definiowany jest obszar po prawej stronie ostatniego punktu. Jest to ustawienie domyślne.
Nachylenie stałe	Definiuje linię stałego nachylenia w wybranym obszarze. Wartość nachylenia jest równa wartości nachylenia pierwszego sektora krzywej, o ile definiowany jest obszar po lewej stronie pierwszego punktu lub wartości nachylenia ostatniego sektora krzywej, o ile definiowany jest obszar po prawej stronie ostatniego punktu.
Modulo	Definiuje wartość w zakresie definicji prawa (wszystkie sektory zdefiniowane) zgodnie z zasadą modulo - zdefiniowana krzywa jest powtarzana po obydwu stronach osi rzędnych. Symulacja dynamiczna sprawdza, czy współrzędne ostatniego punktu prawa (ostatni sektor) są równe współrzędnym pierwszego punktu (pierwszy sektor). Jeśli tak nie jest, wyświetlany jest komunikat o błędzie wskazujący na potrzebę zmiany wartości. Przyczyną wyświetlenia komunikatu jest brak obsługi nieciągłości przez system obliczeniowy. Ten tryb jest stosowany po prawej i lewej stronie prawa.
Cykliczne	W tej funkcji używany jest cykl przekopiowany z punktu zdefiniowanego przez użytkownika, aż do ostatniego punktu krzywej zdefiniowanej przez użytkownika. Na początku cyklu należy wybrać punkt równy ostatniemu punktowi krzywej zdefiniowanej przez użytkownika. W innym wypadku dochodzi do nieciągłości pomiędzy początkiem a końcem cyklu. Wyświetlony zostaje komunikat o błędzie.
Swobodne	Brak definicji tego obszaru. Nie jest przykładana żadna siła i sterowany (ruchem wymuszonym) stopień swobody staje się swobodny. W wypadku ruchu wymuszonego konieczne jest uwolnienie prawego sektora ostatniego punktu przed uwolnieniem ostatniego sektora, przedostatniego itd.