对于自由度非常低的问题,将准确评估行列式,给出 N 次 (N 为不受约束的自由度数目)多项式( 的多项式)。
的多项式)。
将有 N 个实根, 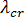 等于这些根中的最小(量级)值。将
等于这些根中的最小(量级)值。将 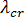 带回挫曲等式将启用临界挫曲位移模式。此模式被定义为一组随意缩放的位移,与挫曲期间发生的配置更改对应。因此,如果要查看结构的挫曲后配置,则需要在结构未变形的配置上叠加与
带回挫曲等式将启用临界挫曲位移模式。此模式被定义为一组随意缩放的位移,与挫曲期间发生的配置更改对应。因此,如果要查看结构的挫曲后配置,则需要在结构未变形的配置上叠加与 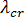 相关联的临界位移模式。
相关联的临界位移模式。
对于具有很多个自由度的结构,展开行列式再提取根的方法是行不通的。要利用更为普遍的求解算法,必须确定带有广义特征问题的挫曲方程。共有 N 个与此特征问题相关的真实特征对 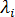 ,
,  ,其中 i = 1, ... N,
,其中 i = 1, ... N, 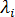 和
和  分别是第 Ith 个特征值和特征矢量,代表第 Ith 个临界载荷系数和挫曲位移模式。可以采用功能强大的通用方法解决广义特征问题。这里采用的方法称为子空间迭代法 [1]。
分别是第 Ith 个特征值和特征矢量,代表第 Ith 个临界载荷系数和挫曲位移模式。可以采用功能强大的通用方法解决广义特征问题。这里采用的方法称为子空间迭代法 [1]。
通过子空间迭代法,可以求解出一系列特征对(设为 n 个),它们按 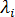 的大小递增排列,即,
的大小递增排列,即,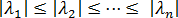 如下所示
如下所示 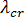 =
=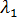 和
和  =
= 。
。
要求解的特征值个数是一个可在翘曲或应力分析期间指定的参数。但请注意,随着所需特征对解个数的增加,所涉计算量也会明显增加。而且在挫曲问题中,通常只关注“真实”临界状态而非假定的高阶模式。虽然在载荷递增的情况下,结构从最初的临界模式更改(通常通过分叉)为另一高阶模式并非罕见,但假定后一模式对应的载荷级别和挫曲变形与预测的最初模式在意义上相关就完全错误(而且十分危险)。这是因为从低阶挫曲模式转换为高阶挫曲模式期间,结构配置可能发生较大变化,从而与挫曲分析的基本假设形成明显冲突。
预测特征值的符号
请注意, 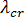 的值没有限制,正值和负值均可。因此,如果
的值没有限制,正值和负值均可。因此,如果 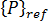 处于选定状态,从而在平板创建拉伸应力字段,
处于选定状态,从而在平板创建拉伸应力字段, 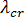 将为负值。另一方面,反转
将为负值。另一方面,反转 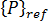 的方向,这样应力状态为压缩状态,
的方向,这样应力状态为压缩状态, 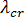 的值将为正值。然而根据定义,两个
的值将为正值。然而根据定义,两个  值的量将完全相同。如果加载参考
值的量将完全相同。如果加载参考 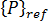 可逆,则实际上它可以独自查找第一个特征对(这是因为我们知道
可逆,则实际上它可以独自查找第一个特征对(这是因为我们知道 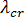 何时为负值,反转
何时为负值,反转 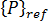 的方向仅仅转换了
的方向仅仅转换了 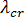 的符号)。但考虑不可逆转载荷系统时将面临一些困难。在这种情况下,挫曲将对应最小的正特征值,由于无法预知负特征值的个数,因此必须在反复试验的基础上继续进行,或者执行至少需要两个特征对的单个分析。体验最新不可逆加载系统(例如,作用于塑料零部件的收缩张力)表明前两个特征对方案通常就足够了(
的符号)。但考虑不可逆转载荷系统时将面临一些困难。在这种情况下,挫曲将对应最小的正特征值,由于无法预知负特征值的个数,因此必须在反复试验的基础上继续进行,或者执行至少需要两个特征对的单个分析。体验最新不可逆加载系统(例如,作用于塑料零部件的收缩张力)表明前两个特征对方案通常就足够了(  值全是正值,或者一个值为负,另一个值为正)。
值全是正值,或者一个值为负,另一个值为正)。
Sturm 序列检查
使用子空间迭代法时偶尔可能跳过一个或多个特征值,因为实际存在的一个或多个特征值可能从预测值中丢失。为此,可使用称为 Sturm 序列检查的技术检查丢失的特征值。遗憾的是,当 n 个特征值中存在任何负值时,该检查无效。
挫曲结果的有效性
执行挫曲分析时,必须牢记初始假设的限制特性。如果执行挫曲之前形状变化巨大,则结果不可靠,因为当前应用的方法超出了其有效性范围。通常,这意味着将高估 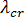 的值,但并总是如此。如果有证据表明结构的预挫曲位移并不小,则应始终在挫曲分析后执行完整的大变形分析。
的值,但并总是如此。如果有证据表明结构的预挫曲位移并不小,则应始终在挫曲分析后执行完整的大变形分析。
挫曲类型
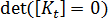
-
极限点。
-
分叉。
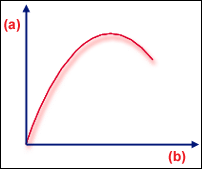
极限点
.(a) 载荷,(b) 变形
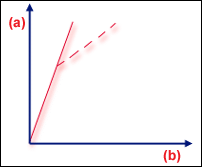
理想结构的分叉
.(a) 载荷,(b) 变形
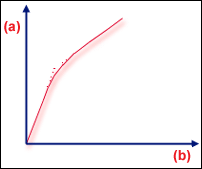
真实结构的分叉
.(a) 载荷,(b) 变形
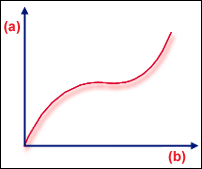
先软化再硬化
.(a) 载荷,(b) 变形
笼统地说,极限点是零部件可接受在形状没有重大变化的情况下的最大载荷状态位置(极限点)。这通常发生在中央载荷可能导致圆顶出现“跳跃”的圆顶型零部件中。一般地说,当挫曲点前面具有明显的几何非线性时,我们认为挫曲为极限点类型。在圆顶示例中,刚度矩阵行列式变为零之前,该零部件必须是非常扁平的。出现“跳跃”(可能轻微,也可能严重)之后,该零部件可以接受更多载荷,但一般来说设计该零部件时必须确保预期载荷不会达到极限点。
分叉是两个可能平衡状态紧挨在一起的“分支”点。如果考虑完全对称的平板,则该平板对平面内压缩载荷的响应完全呈线性。但载荷超出临界值后,平衡立即变得不稳定;就像放置在山顶的球一样,它会以怎样的方式滚下呢?因此真实平板将在该临界载荷级别出现挫曲。因而,有两种可能的平衡路径,我们将其交叉点称为“分叉点”“”(理想结构的分叉)。
这两种类型的挫曲都可出现在翘曲或热载荷问题中,但分叉更为常见。在平板示例中,平面内的瑕疵会导致分叉点处的刚度急剧变化变得模糊(真实结构的分叉)。另一种常见响应是“先软化再硬化”“”(先软化再硬化)。在这种情况下, 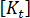 的行列式将变为非常小的值,但不为零。
的行列式将变为非常小的值,但不为零。
像理想结构的分叉和真实结构的分叉的挫曲分析实例通常可以较好地指示分叉位置。像极限点的分析实例则容易过度预测极限点。在类似先软化再硬化的问题中,虽然没有明确的挫曲载荷,但挫曲分析通常会指出非线性开始变得严重的位置。
参考
1. Bathe K.J. 所著《Finite Element Procedures in Engineering Analysis》,Prentice-Hall,Englewood Cliffs,New Jersey。1982 年。第 666-696 页。