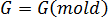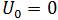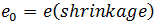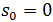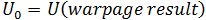此应力分析建立在通过翘曲分析确定的变形零件基础上。
“我们将其称为”“初始条件分析”。此分析使用通过翘曲分析确定的变形和收缩应变作为应力分析的起点。
初始条件分析可用于前面部分介绍的三种分析类型中的任意一种。在本部分中,我们首先介绍如何将翘曲结果转换到应力分析,然后探讨初始条件分析如何与主要的分析类型一起使用。这些分析类型包括:小变形分析、挫曲分析、大变形分析和模型频率分析。
如果规定:
-
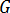 = 模型几何
= 模型几何 -
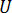 = 位移
= 位移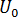 = 初始位移
= 初始位移 -
 = 应变
= 应变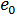 = 初始应变
= 初始应变 -
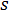 = 应力
= 应力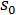 = 初始应力
= 初始应力
那么,我们可以将翘曲分析的输入与初始条件应力分析的输入进行如下比较:
翘曲分析:
初始条件应力分析:
上述比较中需关键注意的是不使用初始应力实现“翘曲中的残余应力”。“”而是通过 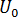 和
和 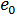 执行。在应力分析的第一步中,FENAS 会有效地重复翘曲分析最后一步中执行的应力计算。此过程不会产生费用,因为应力始终在大变形分析开始时计算。
执行。在应力分析的第一步中,FENAS 会有效地重复翘曲分析最后一步中执行的应力计算。此过程不会产生费用,因为应力始终在大变形分析开始时计算。
另一种(简化)方法是将翘曲形状
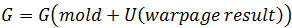
和初始应力 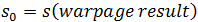 转换到初始条件应力分析。
转换到初始条件应力分析。
使用上述方法可以达到相同的效果,而且具有以下优势:
-
在这两个分析中采用一致的应变定义(应变=变形/长度),因为几何数据 (
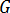 ) 无变化。为了说明这一点,未对翘曲零件施加载荷。所采用的方法没有预测到响应,即没有移动。此结果与使用初始应力方法时有所不同,因为后者中的应变定义会发生变化,即通过“人为重新分布”应力来应对定义的变化。“”
) 无变化。为了说明这一点,未对翘曲零件施加载荷。所采用的方法没有预测到响应,即没有移动。此结果与使用初始应力方法时有所不同,因为后者中的应变定义会发生变化,即通过“人为重新分布”应力来应对定义的变化。“” -
通过减小应力分析中的弹性模量,可以方便地按比例减小翘曲分析中的残余应力。“可以使用应力分析中减小的”弹性模量粗略模拟翘曲中残余应力减小的效果,并允许在载荷作用下缓慢移动(可使用“有效的线性模量”)。
例如,如果对翘曲采用 E1=1600,E2=1200 MPa;对外部载荷采用 E1=800,E2=600 MPa;则外部载荷分析第一步开始时计算得到的应力为翘曲分析结束时残余应力输出的一半。因此可将“减小的残余应力”转换到外部载荷分析中。“”使用初始应力方法则无法轻松实现此点。
-
后处理得到简化,因为无需通过将初始应力添加到结构或翘曲分析的应力来生成最终应力。
初始条件和三种分析类型
本部分包括一些与各种分析类型一起使用初始条件分析时的具体注释。
- 挫曲分析
-
运行挫曲分析时,将执行两个分析;首先执行小变形分析,然后执行挫曲分析。
通常采用线性(经典)挫曲方法。初始小变形分析用于确定 100% 载荷下的零件配置。然后,挫曲分析使用 0 载荷和 100% 载荷下的已知配置。对结果执行后处理时,可以检查 100% 载荷下的偏移形状,以及通过挫曲分析确定的模式形状。
但对于具有初始条件的挫曲分析,经典线性挫曲理论则不能用于该问题,因为施加载荷前应力不为零。因此必须使用“线性化挫曲”方法。“”在此方法中,初始小变形分析用于确定极小百分比载荷下的零件配置。然后,线性化挫曲分析使用 0% 载荷下和此小百分比载荷步结束时的已知配置。
注: 也就是说,对初始条件挫曲分析结果进行后处理时,100% 载荷下的偏移形状不可用。只能显示模式形状。如果需要线性结果,需要运行小变形分析和挫曲分析。
由于通过挫曲分析确定的模式形状是一个增量模式形状(挫曲点的配置变化),因此必须将其与翘曲形状叠加(经过适当缩放后)。
- 大变形分析
-
注: 应只对大变形翘曲结果执行大变形初始条件应力分析。
仅当已知翘曲响应的线性度非常高(即挫曲分析的特征值非常高)时,才能使用大变形翘曲分析结果。
- 模型频率分析
-
模型频率分析也可以使用翘曲分析的初始条件。在此采用与初始条件挫曲分析类似的注释。
包括初始条件的影响
翘曲中的应力可对载荷作用下的零件造成稳定或失稳影响。例如,如果残余应力造成细长曲面压缩,则会有效增加由压缩载荷引起的应力。在此情况下,不包括初始条件的分析将过度预测破坏载荷。
或者,如果翘曲应力造成伸张,压缩载荷可能抵消残余应力,因此不包括初始条件的分析将过于保守地预测破坏载荷。
规定位移和初始条件
本软件非常有用的一个功能是可以在初始条件分析中规定位移(而不是施加载荷)。这样便可以确定使翘曲形状变形为已知配置需要多大的力。最终结果还将显示强制零件变成该配置所产生的应力。
对于已应用规定位移边界条件的各个节点,FENAS 将在结果摘要文件中输出“反作用力”。“”
应力结果能否用作初始条件?
以下两个示例说明在哪些场合下准备基于应力分析的初始条件分析非常有用:
-
已使用规定位移应力分析将翘曲零件强制成形。此外希望获取该零件对其他外部载荷的响应。
-
已向零件施加外部载荷。此外希望获取该零件对热载荷的响应。
但基于以下原因,不能在此版本中将结构结果用作其他应力分析的初始条件。
翘曲分析结果可以用作应力分析的初始条件,因为翘曲分析的约束反作用接近于零。对于外部载荷的应力分析,其中的约束反作用并非全部为零,必须将这些反作用传递到第二个分析中。如果不传递这些反作用,可能违背平衡要求,尤其是移动约束时。
在此版本中,不存在将约束反作用从第一个分析传递到第二个分析的机制。为此,应力分析程序不允许使用应力分析结果文件作为初始条件。