如果某个结果的载荷逐步增加,则该结构的配置很有可能从某一级别的载荷开始,改变速度比以前大大加快。
在相关的载荷-变形路径上,这种情况很容易识别,其特点是所在部分的斜率和/或曲率有明显变化。通常这种变化为软化类型,即,斜率减小而位移增加的速度比以前更快,同时形状发生显著变化。这种行为总称为挫曲。挫曲分为两种主要类型,分别为完美结构和有缺陷的结构的挫曲。
完美结构的挫曲
随着载荷的增加,完美结构最初会跟随其在稳定性和挫曲:直立柱、稳定性和挫曲:平板和稳定性和挫曲:圆柱壳中的主要(或基本)平衡路径 AB。在此阶段期间,结构的刚度在其最弱的方向(即侧向或平面外方向)会不断降低。在 B 点(称为分叉点),结构会跟随阻力最小的(当前)路线发生挫曲。这种形式的挫曲可看作从硬膜(轴向)主导路径向柔性弯曲主导路径的过渡。由于细长柱体以及薄壁的板和壳在轴向要比弯曲方向硬得多,它们自然最容易发生挫曲。
稳定性和挫曲:直立柱、稳定性和挫曲:平板和稳定性和挫曲:圆柱壳中的路径 BC 称为次要路径或后挫曲路径。分叉后的结构稳定性通过 B 点的次要路径斜率体现。因此,B 点处的平衡状态为中性(稳定性和挫曲:直立柱)、稳定(稳定性和挫曲:平板)和不稳定(稳定性和挫曲:圆柱壳)。
在不稳定的情况下,增加任意小的载荷都将导致结构立即跳到邻近的稳定平衡配置(例如,稳定性和挫曲:圆柱壳中的虚线路径 BD)。这种现象称为跳跃翘曲。请注意,稳定性和挫曲:圆柱壳中的实线曲线路径 BCD 所描述的另一个后挫曲路径描绘了理论平衡状态(阻止跳跃时出现),并且载荷会逐渐减少,直到在点 C 再次获得稳定路径。
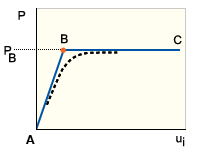
稳定性和挫曲:直立柱
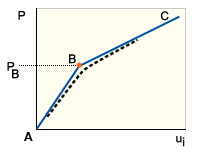
稳定性和挫曲:平板
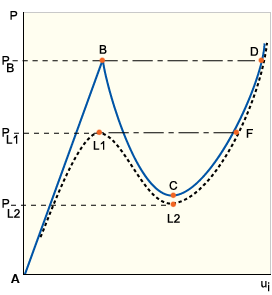
稳定性和挫曲:圆柱壳
显然,从设计者的角度来看,最好获得稳定的后翘曲路径,并且如果位移可以接受,经常会对可用后翘曲力的增加进行利用。在另一方面,不稳定的平衡路径很少可被接受,尤其是它通常会伴随有动态跳跃。此外,呈现不稳定挫曲的结构经常对缺陷很敏感,即,最大或临界载荷能力对初始缺陷大小和形状的微小变化很敏感。
有缺陷的结构的挫曲
真实结构永远不可能是完美结构。即使几何、载荷、边界条件或材料属性的微小扰动通常也会阻碍真分叉的形成。主要路径和次要路径曲线会在局部形成一个连续且唯一的解,而不会相交形成斜率不连续性。生成的后挫曲路径由稳定性和挫曲:直立柱、稳定性和挫曲:平板和稳定性和挫曲:圆柱壳中的虚线来描述。随着缺陷程度的减小,曲率的变化将变得更加局部化。在完美结构会呈现不稳定分叉点的位置,有缺陷的结构会呈现极限点( 稳定性和挫曲:圆柱壳中的点 L1)。
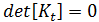
在后挫曲路径的更远处可能会遇到第二个极限点,但这一次它将是载荷-变形曲线上的最小值( 稳定性和挫曲:圆柱壳中的点 L2)。请注意,类似于完美结构,不稳定路径 L1L2 实际上不会被跟随。相反,将发生由点划线路径 l1F 描述的立即跳跃挫曲。尽管完美结构的挫曲通常包含分叉,但这绝不意味着总是如此。相反,只要预挫曲模式形状包含由于所施加的边界条件而无法打破的对称性,都可能出现经过极限点的不稳定挫曲。因此,分叉挫曲有时被称为对称性破坏。
分析注意事项
对包含对称性的完美结构执行非线性增量分析时,有必要为结构分配一个小缺陷以打破对称性。如果不这样做,解很可能沿着基本平衡路径继续,而不是分支到真后挫曲路径。可能发生这种情况的示例是共轴载荷下的直立柱以及平面内载荷下的平板。对没有冷却分析结果的平直零件执行翘曲分析时,可实现后一个示例。这种情况下的推荐流程是嵌入一个形状与预期挫曲模式形状相对应的微小几何缺陷。(如果挫曲模式形状未知,则可以使用任何平面外形状。)