在結構分析中使用的元素類型 (概念)

針對中間平面與 Dual Domain 分析技術，結構分析提供薄殼與樑元素。

薄殼元素

薄殼元素使用平面直邊三角形的形式。當為彎曲薄殼塑型時，它們提供對於真實幾何圖形的"「面」逼近。"目前，每個元素的厚度都假設為恆定，但鄰接元素的厚度可能不同。

在所有情況下，都會在每個節點上使用六個位移自由度。這包括平行於全域軸的三個平移與繞這些軸的三個旋轉。對於平滑薄殼而言，可能只會使用五個自由度，亦即中間平面法線的三個平移與兩個局部旋轉。但是，在所有情況下使用六個自由度會有明顯的優點。首先，它可以在未對相交表面之間的接合處套用任何特殊約束條件的情況下分析非平滑結構 (例如盒子、盤子及硬薄殼)。其次，樑元素 (在三維空間中必須有六個自由度) 可以直接連接至基本板或薄殼網格的節點，而不套用約束或轉換。第三，在較大撓曲 (從幾何來講為非線性) 分析中，使用三個旋轉自由度可針對有限剛體運動引入簡練且從幾何角度而言完全正確的模型 [1-3]。薄壁結構的現有幾何非線性模型有許多缺陷，但並不值得追蹤針對旋轉參數所進行的逼近。此處所採用的參數是"「自然」的，它的意思是說，這些參數直接與相關聯的旋轉張量的光譜分析相關。"若要獲得線性化形式，請使用 Euler 與 Rodriques [1,3,4] 的剛體運動傳統分析。

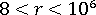
元素公式可說明薄膜、彎曲及橫向剪切變形。後者以 Reissner-Mindlin 理論 [5,6] 為基礎。在此理論中，薄板與薄殼的傳統 Kirchhoff 假設透過將連續性需求從 C₁ 降低到 C₀ (包括橫向剪切) 來解除。這將會允許為"「較薄」及「適中」厚度的板與薄殼塑型。"""實際上，當板或薄殼變薄時，此類元素的效能已知快速下降。此現象稱為剪切鎖定，因元素無法在適當的二次率之下達到零橫向剪切應變的限制條件所導致。剪切鎖定可透過使用減少的積分來緩解，但與早期的預期 [7] 相較，它一點都沒有消除。最近由 Fried [8] 與 McNeal [9] 提出的能量平衡技術變體版本產生了極佳的結果，超越了大範圍的結構縱橫比 (圍繞薄殼結構的中間平面測量的特徵尺寸與平均壁厚度之比)。用於表示三角形元素的形式由 Tessler 與 Hughes [10] 提出，可允許比逼近縱橫比範圍獲得更精確的結果：

除了消除鎖定以外，此方法還降低了薄殼對元素變形的敏感度，並改善了勁度矩陣的條件與應力預測的品質。

註: 薄膜鎖定的類似問題只發生於薄彎曲元素中，因此不需要在此考慮。

目前只能為線性彈性材料塑型。它們可能是等向性或正向性的。在後者的情況下，材料的主平面為正向性，一個平面位於薄殼的中間平面，其他兩個平面沿兩條垂直線與此表面相交，這兩條線就是正向性的方向。正向性的方向由製程決定，並針對「充填與保壓」分析中的每一個元素指定。每個方向的材料性質由使用者在為翹曲或應力分析準備分析輸入檔案時指定。

幾何非線性以對流的 Lagrangian 方法為基礎，在此位移場即為一組在每個點上與薄殼的剖面共同旋轉的局部對流座標。為了達到一致性，通常無法伸展的情況會在此套用到在任何一點上與剖面指標共線的纖維。

從連續介質力學的極分解定理中導出的共同旋轉方法主張任何一般空間運動都始終可以分解成純拉伸 (變形)，後跟剛體運動。採用適當的有限旋轉方法 (見上) 與明確捨棄整體運動的剛體元件，便可達成在元素內對內部變形與相關聯的應力進行評估的一致方法。實際上，這表示無需對剛體運動的強度加以任何限制，而決定內部變形與應力的準確度將在整個分析中保持一致。

公式與 Reissner [11,12]、Simmonds 與 Danielson [13]、Danielson 與 Hodges [14] 的有限撓曲理論及 Bates [1]、Simo 與 Vu-Quoc [15] 的的這些理論的有限元素實作緊密相關。

元素 LMT3

元素 LMT3 在中間平面分析技術中使用。LMT3 是具有 18 個自由度 (每個節點上六個) 的三節點三角形元素。此元素的建構方式是加上 Bergan 與 Nygard [16] 及 Bergan 與 Felippa [17] 的局部薄膜公式，以及 Tessler 與 Hughes [10] 的彎曲公式，並將結合方程式轉換為全域座標系來完成的。產生的元素可為薄膜的雙線性變化及橫向剪切應變塑型，但彎曲應變 (曲率) 為恆定。

Bergan 與 Nygard 的"自由公式"以假設的位移場為基礎，但已超出嚴格的潛在能量公式在允許使用"非標準"形狀函數方面的要求。為了確保收斂，修補測試需求為強迫先驗。位移形狀函數可分為基本與較高級模式，前者與剛體及恆定應變狀態相關聯，而後者與座標不變平面內彎曲模式相關聯。

這會分別導致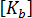

與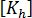

所表示的基本與較高級勁度。然後結合薄膜勁度會採取以下形式：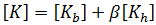

其中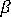，是在較高級勁度上做為比例係數使用的自由參數。與詳細的測試結果一致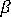， = 1.5 已被採用為最佳選擇。

繞局部中間平面法線旋轉 (通常稱為鑽孔自由) 會由罰約束技術連結至中間平面的平均平面內旋轉。因此，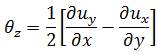

鑽孔自由是公式中完全積分的作用中元件。即使在確實共面的元素中，也會維持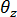與平面內梯度之間的連結強度，以避免再次發生奇異點問題。若要使用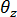做為邊界條件元件，需要特別注意。

元素的彎曲公式基礎是透過連續橫向剪切邊約束 [10] 達成的明確自由度技術。這會導致約束的 (結合的) 總位移場中，在橫向位移 u_z 中具有雙二次變化，而在法向旋轉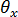與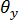中具有雙線性變化。當與橫向剪切修正係數技術 [10] 結合時，元素會在整個縱橫比範圍內展示改善許多的彎曲回應 (相較於標準恆定曲率公式)。

元素定義

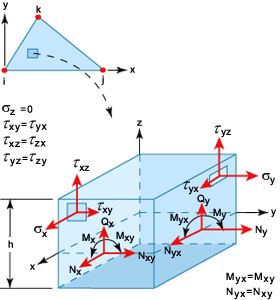
元素的幾何圖形、節點編號與局部/全域自由度顯示在〈LMT3 薄殼元素〉中。請注意，節點 i、j、k 是指在分析輸出檔案中提供的節點連接表中的項目。例如，如果元素的連接為 11、101、85，則 i = 11，j = 101，k =85，且局部 X 軸從節點 11 一直到節點 101。

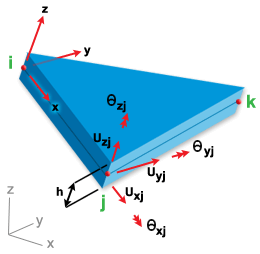
LMT3 薄殼元素

元素負載

有兩種元素負載可用：因正向性收縮所導致的壓力負載與初始應變。

壓力負載假設為對元素中間平面起作用，及法向於元素中間平面。壓力會假設為在任何特定元素上具有恆定值，但在相鄰元素中使用的壓力值可能不同。

積分法則

中間平面上的積分使用三點數值積分法執行。由於材料為線性彈性，且元素平坦，應變與應力會在整個薄殼壁上產生線性的變化。因此，會使用厚度方向的明確預積分，而非更昂貴的數值積分。

積分站位置與重量顯示在〈LMT3 元素的積分站位置〉和〈LMT3 元素的積分位置重量〉中。

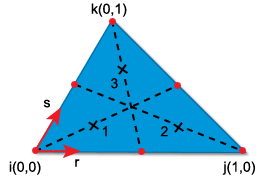
LMT3 元素的積分站位置

LMT3 元素的積分位置重量
元素	積分站	r 座標	s 座標
LMT3	1 2 3	1/6 2/3 1/6	1/6 1/6 2/3

結果輸出

薄膜力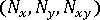、彎曲力矩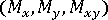與橫向剪切力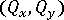會在積分站計算，並顯示在〈LMT3 元素分析中的結果〉中。

這些結果會在分析輸出檔案中重新產生。

LMT3 元素分析中的結果

假設平面應力條件，任何等級 z 的應力得出方法為：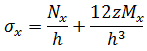

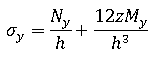
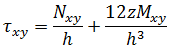
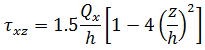請注意，力與力矩會對板或薄殼的單位寬度起作用，因此薄膜與剪切力具有尺寸力/長度，而力矩具有尺寸 (力)。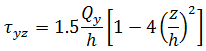

元素 LBT3

元素 LBT3 在 Dual Domain 分析技術中使用。LBT3 是具有 18 個自由度 (每個節點上六個) 的三節點三角形元素。此元素的建構方式是加上 Bergan 與 Nygard 及 Bergan 與 Felippa 的局部薄膜公式，以及 Batoz 的彎曲公式，並將結合方程式轉換為全域座標系來完成的。產生的元素可為薄膜的雙線性變化、彎曲應變與橫向剪切應變塑型。

這會分別導致

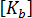與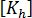

所表示的基本與較高級勁度。然後結合薄膜勁度會採取以下形式：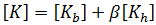

其中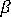，是在較高級勁度上做為比例係數使用的自由參數。與詳細的測試結果一致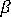， = 1.5 已被採用為最佳選擇。

繞中間平面法線旋轉 (鑽孔自由) 會採取與 LMT3 相同的連續介質力學定義，亦即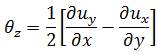

元素的彎曲公式以離散 Kirchhoff 技術的一般化為基礎，以包含橫向剪切影響。元素不會鎖定，並且可用於較厚或較薄零件的分析。如果橫向剪切影響不明顯，它會與知名的 DKT (離散 Kirchhoff 三角) 元素重合。

數值測試指示 LBT3 執行得非常好。一般而言，LBT3 稍微比 LMT3 好一點。此外，單層與多層公式可在 LBT3 中使用，但 LMT3 目前只能用於單層分析。

建議多層 LBT3 用於執行纖維填充塑膠的應力與翹曲分析。在逐層考慮纖維配向的情況下，實體模型比較真實，結果也預期比較準確。

元素定義

元素的幾何圖形、節點編號與局部/全域自由度顯示在〈LBT3 薄殼元素〉中。請注意，節點 i、j、k 是指在分析輸出檔案中提供的節點連接表中的項目。例如，如果元素的連接為 11、101、85，則 i = 11，j = 101，k =85，且局部 X 軸從節點 11 一直到節點 101。

LBT3 薄殼元素

元素負載

有兩種元素負載可用：因正向性收縮所導致的壓力負載與初始應變。

積分法則

積分站位置與重量顯示在〈LBT3 元素的積分站位置〉和〈LBT3 元素的積分位置重量〉中。

LBT3 元素的積分站位置

LBT3 元素的積分位置重量
元素	積分站	r 座標	s 座標
LBT3	1 2 3	1/6 2/3 1/6	1/6 1/6 2/3

結果輸出

薄膜力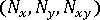、彎曲力矩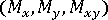與橫向剪切力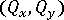會在積分站計算，並顯示在〈LBT3 元素分析中的結果〉中。

這些結果會在分析輸出檔案中重新產生。

LBT3 元素分析中的結果

假設平面應力條件，任何等級 z 的應力得出方法為：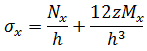

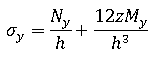
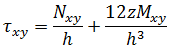
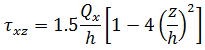
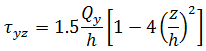
請注意，力與力矩會對板或薄殼的單位寬度起作用，因此薄膜與剪切力具有尺寸力/長度，而力矩具有尺寸 (力)。

樑元素

樑元素 BEAM2 是一個二節點樑，目前適用於中間平面與 Dual Domain 分析技術。

元素的縱軸是直的，因此當為彎曲樑塑型時，它們會提供對於真實幾何圖形的"「面」逼近。"目前，假設樑具有恆定半徑的圓形剖面。但是，相鄰元素的剖面半徑可能不同。

每個節點上使用了六個自由度，亦即平行於全域軸的三個平移及繞這些軸的三個旋轉。在有限旋轉的環境中，旋轉自由度的定義與針對薄殼所討論的定義完全相同。樑與薄殼元素在一或多個節點上的實體連接是直接的。請注意，如果每個樑節點都連接到薄殼節點，為結合的結構塑型所需要的方程式總數便與單獨為自己的薄殼結構塑型所需要的數目相同。因此，加入樑元素所牽涉到的計算負擔通常會相當小。

元素公式可說明軸向、彎曲、扭力及橫向剪切變形。基本假設為，樑剖面會保持平面及未變形，但在存在橫向剪切的情況下，將不會維持法向於縱軸。您可將產生的模型想像成在兩階段中從傳統 Euler-Bernoulli 樑中導出。首先，加入 Reissner-Mindlin 類型剪切模型可說明橫向剪切的平均影響。這會導致產生一般所說的 Timoshenko 樑。在第二階段中，會使用 St.Venant 的理論為扭力行為塑型。

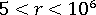
當使用樑元素為流道、肋或獨立樑結構塑型時，縱橫比 (沿樑軸測量的總長度與平均剖面直徑的比) 應在逼近範圍之內：

使用罰鬆弛技術，也可能獲得非常高的上限。儘管樑元素不會出現剪切或薄膜鎖定的現象，此技術也可防止元素勁度矩陣在高縱橫比之下變得條件不良。

目前只能為針對樑元素為等向性線性彈性材料塑型。請注意，要能夠說明一般正向性材料行為，而不與上述的基本假設衝突，是不可能的。

從連續介質力學的極分解定理中導出的共同旋轉方法主張任何一般空間運動都始終可以分解成純拉伸 (變形)，後跟剛體運動。採用適當的有限旋轉方法與明確捨棄整體運動的剛體元件，便可達成在元素內對內部變形與相關聯的應力進行評估的一致方法。這表示無需對剛體運動的強度加以任何限制，而決定內部變形與應力的準確度將在整個分析中保持一致。

公式與 Reissner [11]、Danielson 與 Hodges [14]、Hodges 與 Simo 的有限撓曲理論緊密相關。Bates [1] 與 Simo 與 Vu-Quoc [15] 的這些理論的有限元素實作也有關聯性。

元素 BEAM2

這是在每個節點上具有 6 個自由度的 2 節點樑。假設樑軸是直的，剖面是圓的實心的。元素可以獨立形式使用，或者可連接至三角形薄殼元素 LMT3 的一邊。

公式以線性等參數形狀函數為基礎。若要避免剪切鎖定，可使用減少的積分來求出勁度與內部力，在此情況下是指使用單點高斯數值積分法。產生的模型會展示恆定軸向、彎曲、扭力與剪切應變場。

在其未修改的形式下，預測的元素回應取決於元素的彎曲模式。

針對純彎曲，會在控制積分點取得確切的節點位移與應力結式。

但是，透過套用罰鬆弛方法 [19]，後者的過度勁度會完全消除。也會針對恆定拉伸與扭轉預測確切位移與中心應力結式。

元素定義：

元素的幾何圖形、節點編號與局部/全域自由度顯示在〈BEAM2 樑元素〉中。請注意，節點 i、j 是指在分析輸出檔案中提供的節點連接表中的項目。例如，如果元素的連接為 55、77，則 i = 55，j = 77，且局部 X 軸從節點 55 一直到節點 77。

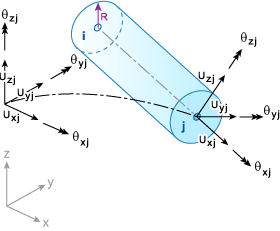
BEAM2 樑元素

元素負載：目前唯一可用的元素負載類型是因收縮而產生的軸向與曲率應變的規格。(但是請注意，濃縮外部負載，亦即力與力矩，可直接套用於有限元素網格的節點上。)

積分法則

內部力 (應力結式) 在〈BEAM2 元素的積分站〉中所示的中心積分點上計算，並在分析輸出檔案中重新產生。

針對線性彈性材料，應變與應力會在樑的剖面上產生線性的變化。因此，會使用剖面上的明確預積分，來取代更昂貴的數值積分。

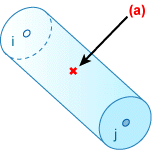
BEAM2 元素的積分站

(a) 積分點。

結果輸出

以下應力結式在積分站上計算，並在分析輸出檔案中重新產生。

力矩：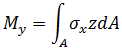

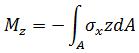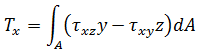扭力：

力：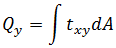

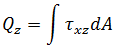
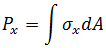
BEAM2 元素分析中的結果

任一點 (y,z) 的應力可如下求得：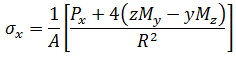

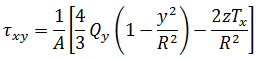
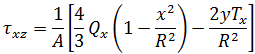
參考文獻

Argyris, J.H., "An excursion into large rotations", Comp. Meth. Appl. Mech. Engrg., Vol. 32, 1982, pp. 85-155.
Rankin, C.C. and Brogan, F.A., "An element independent corotational procedure for the treatment of large rotations", in: Collapse Analysis of Structures (L.H. Sobel and K. Thomas eds.), ASME, New York, 1984, pp.85-100.
Bates, D.N., The mechanics of thin walled structures with special reference to finite rotations, Ph.D. Thesis, University of London, 1987.
Hodges, D.H., "Finite rotation and non-linear beam kinematics", Vertica, Vol. 11, No. 1/2, 1987, pp. 297-307.
Reissner, E., "The effect of transverse shear deformation on the bending of elastic plates", J. Appl. Mech., ASME, Vol. 12, 1945, A69-A72.
Mindlin, R.D., "Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates", J. Appl. Mech., ASME, Vol. 18, 1951, pp. 31-38.
Zienkiewicz, O.C., Taylor, R.L., and Too, J.M., "Reduced integration technique in general analysis of plates and shells", Int. J. Num. Meth. Engrg., Vol. 3, 1971, pp. 275-290.
Fried, I., "Residual energy balancing technique in the generation of plate bending finite elements", Comp. and Struct., Vol. 4, 1974, pp. 771-778.
McNeal, R.H., "A simple quadrilateral shell element", Comp. and Struct., Vol. 8, 1978, pp. 175-183.
Tessler, A. and Hughes, T.J.R., "A three-node Mindlin plate element with improved transverse shear", Comp. Meth. Appl. Mech. Engrg., Vol. 50, 1985, pp. 71-101.
Reissner, E., "On one-dimensional large-displacement finite-strain beam theory", Stud. Appl. Math., Vol. 52, 1973, pp. 87-95.
Reissner, E., "Linear and non-linear theories of shells, in: Thin Shell Structures" (Y.C. Fung and E.E. Sechler, eds.), Prentice-Hall, Englewood Cliffs, New Jersey, 1974, pp.29-44.
Simmonds, J.G. and Danielson, D.A., "Non-linear shell theory with finite rotation and stress-function vectors", J. Appl. Mech., ASME, Vol. 39, 1972, pp. 1085-1090.
Danielson, D.A. and Hodges, D.H., "Non-linear beam kinematics by decomposition of the rotation tensor", J. Appl. Mech.,ASME, Vol. 54, 1987, pp. 258-262.
Simo, J.C. and Vu-Quoc, L., "A three-dimensional finite strain rod model.Part II: Computational aspects", Comp. Meth.Appl. Mech. Engrg., Vol. 58, 1986, pp. 79-116.
Bergan, P.G. and Nygård, M.K., "Finite elements with increased freedom in choosing shape functions", Int. J. Num. Meth. Engrg., Vol. 20, 1984, pp. 643-664.
Bergan, P.G. and Felippa, C.A., "A triangular membrane element with rotational degrees of freedom", Comp. Meth. Appl. Mech. Engrg., Vol. 50, pp. 25-60.
Nygård, M.K., The free formulation for non-linear finite elements with applications to shells, Report No. 86-2, Division of Structural Mechanics, The Norwegian Institute of Technology, Trondheim, 1986.