Das Konzept des kontrollierten Chaos ist ein Grundzug des Partikelsystems. Um Chaos auf einen Datenoperator anzuwenden, verwenden Sie den Zufalls-Unteroperator. Der Zufalls-Unteroperator generiert mithilfe verschiedener Algorithmen zufällige Werte in Skalar- und Vektor-Formaten. Näheres dazu erfahren Sie in diesem Abschnitt.
Überprüfen von Zufallsbeispielen
Beginnen wir mit einem Beispiel, wie Partikel chaotisch um ein Referenzobjekt platziert werden können: Siehe dazu die mitgelieferte Datei RandomPositioning.max .
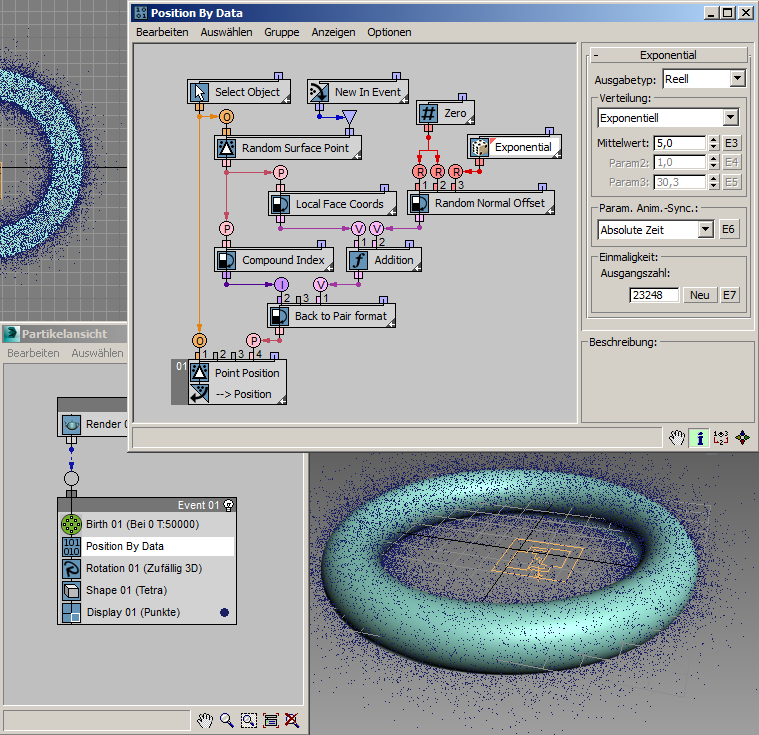
Im oben dargestellten Datenfluss verteilt der Geometrie-Unteroperator (1.) zufällige Punkte gleichmäßig auf der Oberfläche eines Referenzobjekts. Seine Paar-Datenausgabe wird anschließend in zwei verschiedene Konvertierungs-Unteroperatoren geteilt: Lokale Koordinaten der Fläche (2.) und Verbundindex (3.) Dieser umfasst auch den Flächenindex mit der Position eines zufälligen Punkts.
Um die gewünschte Verteilung der Partikel um das Referenzobjekt zu erreichen, müssen die Partikel von der Oberfläche "abgehoben" werden. Dies erfolgt durch Ändern der Z-Komponente des lokalen Koordinatenvektors der Fläche. Die Z-Komponente ist der Abstand von der Fläche in Richtung der Flächennormalen.
Mit dem Zufalls-Unteroperator (4.) können Sie angeben, wie weit die Partikel "abgehoben" werden sollen. In diesem Beispiel verwenden wir eine Exponentialverteilung. Sie ist positiv und dichter rund um null. Dementsprechend werden nahe an der Oberfläche mehr Partikel platziert, und die Dichte nimmt mit zunehmendem Abstand von der Oberfläche ab.
Anschließend werden der bearbeitete Wert für die lokalen Koordinaten der Fläche und der Verbundindex in das Paar-Datenformat zurückkonvertiert, das vom Geometrie-Unteroperator (5.) verwendet wird, um die Position der Partikel in den Weltkoordinaten zu berechnen.
Werfen wir einen näheren Blick auf den Parameter Verteilung des Zufalls-Unteroperators. Der Parameter definiert den Typ der Zufallsfunktion, die vom Unteroperator eingesetzt wird. Der Funktionstyp hängt auch vom Datentyp ab, den der Zufalls-Unteroperator erzeugt.
Für die nächste Beschreibung öffnen Sie die mitgelieferte Szenendatei RandomTemplate.max , in der Sie verschiedene Verteilungsfunktionen ausprobieren können.

Sie beginnen mit einem einfachen Verteilungstyp: Gleich (diskret). Wenn der Zufalls-Unteroperator auf den Datentyp Ganzzahl gesetzt ist, ist nur dieser Verteilungstyp verfügbar. Diskret ist hier das Gegenteil von stetig. Der Zufalls-Unteroperator generiert ganzzahlige Daten (in diesem Sinn also einzelne, diskrete Daten), die zwischen den in der Benutzeroberfläche definierten minimalen und maximalen Werten gleichmäßig verteilt werden. Im nächsten Beispiel ( RandomTemplate01.max ) sind der minimale und der maximale Wert auf 0 bzw. 30 gesetzt. Sie können also sehen, dass die Partikelpositionen entlang der X-Ordinaten verteilt werden: 0, 1, 2, 3 usw. bis zu 30. Hier erfahren Sie mehr über die Grundlagen der diskreten Gleichverteilung.
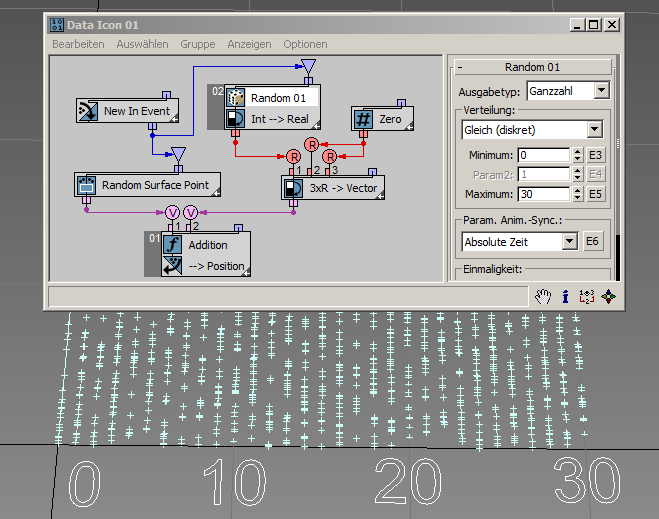
Der Datenausgabetyp Reell bietet die größte Auswahl an verfügbaren Verteilungstypen.
Der Verteilungstyp Gleich ist dem Typ Gleich (diskret) einzeln sehr ähnlich; auch hier dienen minimale und maximale Werte zum Definieren der Verteilung, aber die Ausgabewerte werden nun stetig über den Bereich verteilt. Hier erfahren Sie mehr über die stetige Gleichverteilung.
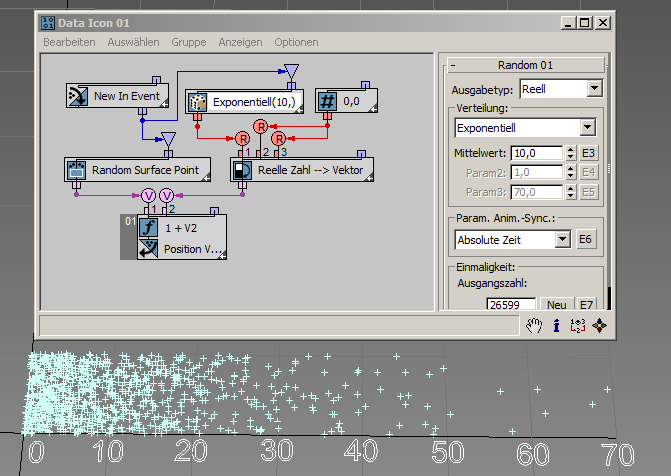
Die Option für die Exponentialverteilung kommt gewöhnlich in der Zuverlässigkeitstechnik zum Einsatz. Sie kann verwendet werden, um das Verhalten von Einheiten mit einer wirklich zufälligen konstanten Ausfallrate zu modellieren. Ein weiteres Beispiel für die Exponentialverteilung ist die Verteilung der einzelnen Lebensdauern instabiler Partikel beim radioaktiven Verfall.
Die Exponentialverteilung generiert ausschließlich positive Werte. Etwa die Hälfte der erzeugten Werte ist kleiner als der Parameter für den Mittelwert, und eine höhere Anzahl von Werten befindet sich nahe null. Ein generierter Wert kann beliebig hoch sein. Je höher aber der Wert, desto geringer die Wahrscheinlichkeit, dass er tatsächlich generiert wird. In diesem Beispiel ( RandomTemplate02.max ) beträgt der Mittelwert 10; das bedeutet, dass die meisten generierten Werte zwischen 0 und 70 liegen. Hier erfahren Sie mehr über die Exponentialverteilung.
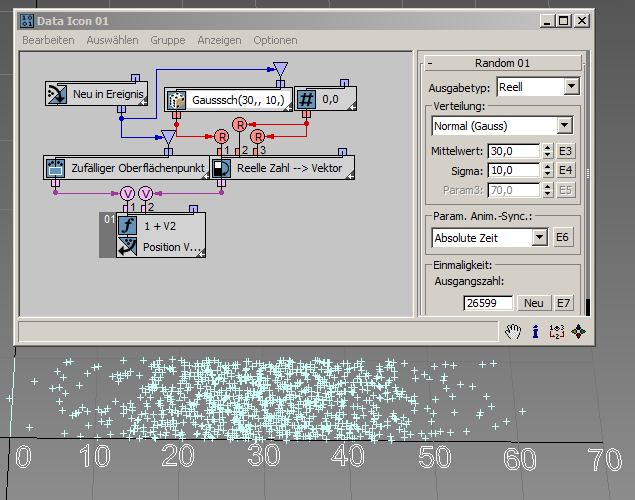
Die Normal- oder Gauß-Verteilung beschreibt die Verteilung unabhängiger zufälliger Messfehler. Andere Vorkommen einer Normal- oder Fast-Normalverteilung sind Körpertemperatur, Schuhgrößen, Durchmesser von Bäumen usw. Das Diagramm einer Normalverteilung ist eine symmetrische Glockenkurve. Der Mittelwert-Parameter definiert den Durchschnittswert der berechneten Werte (die Mitte der Glockenkurve) und der Sigma-Parameter bestimmt, wie weit die generierten Werte außerhalb des Mittelwerts fallen dürfen. Die meisten Werte (99,7 %) werden innerhalb des 3-Sigma-Abstandsintervalls [Mittelwert3*Sigma, Mittelwert + 3*Sigma] erzeugt. Im folgenden Beispiel ( RandomTemplate03.max ) beträgt der Mittelwert-Parameter 30 und der Sigma-Parameter 10, wodurch die Mehrzahl der generierten Werte in das Intervall [0.0, 60] fallen. Die Normalverteilung erzeugt negative und positive Werte. Ein generierter Wert kann beliebig hoch sein. Je höher aber der Wert, desto geringer die Wahrscheinlichkeit, dass er tatsächlich generiert wird (siehe die 3-Sigma-Regel oben). Hier erfahren Sie mehr über die Normalverteilung.
Die Dreiecksverteilung ist eine vereinfachende Methode zur Beschreibung eines zufälligen Phänomens, das gegen einen Spitzenwert tendiert und dessen Bereich durch minimale und maximale Werte festgelegt ist. In diesem Beispiel ( RandomTemplate04.max ) emuliert die Dreiecksverteilung die Normalverteilung aus dem vorherigen Beispiel. Hier erfahren Sie mehr über die Dreiecksverteilung.
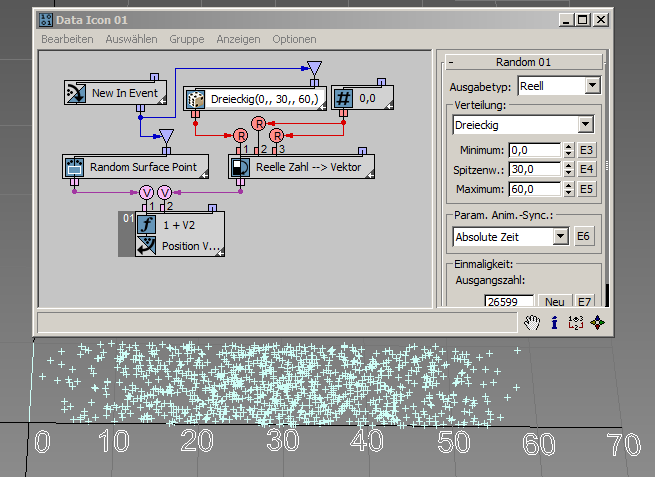
Die Weibull-Verteilung erweitert die Exponentialverteilung auf Ereignisse, die nicht rein zufällig sind; sie wird häufig bei der Modellierung von Zuverlässigkeit und Lebensdauer bzw. Ermüdung von Materialien eingesetzt. In diesem Beispiel ( RandomTemplate05.max ) ist der Parameter Rate gleich 1.0, sodass die Weibull-Verteilung der Exponentialverteilung entspricht, mit dem Mittelwert als Weibull-Skalierungsparameter.
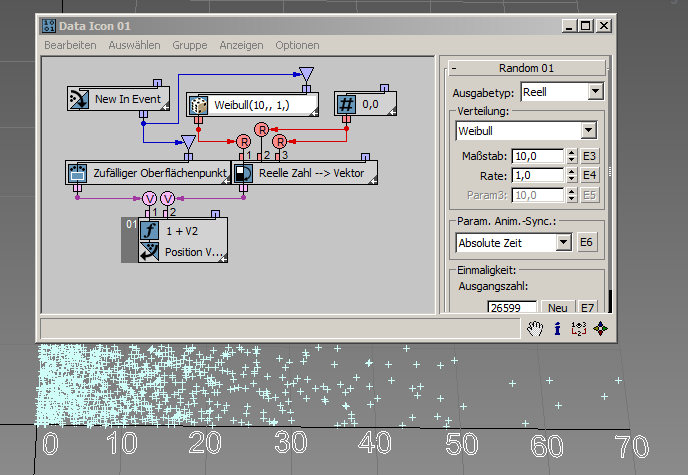
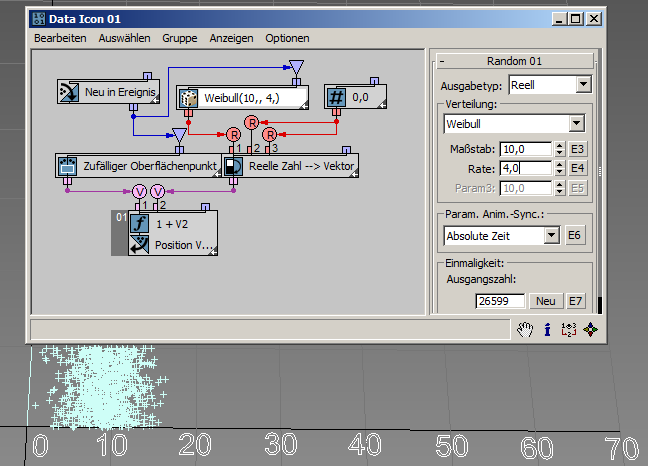
Sie können mit der Weibull-Verteilung ein Modell des Zeitraums bis zum Ausfall eines bestimmten technischen Geräts anfertigen. Wenn die Ausfallrate des Geräts mit der Zeit geringer wird, legen Sie Rate < 1 fest. Wenn die Ausfallrate des Geräts mit der Zeit steigt, legen Sie Rate > 1 fest. Die Weibull-Verteilung kann auch verwendet werden, um die Verteilung von Windgeschwindigkeiten an einem bestimmten Ort auf der Welt zu modellieren. Dabei hat jeder Ort eigene Parameter für Rate und Skalierung. In diesem Beispiel ( RandomTemplate06.max ) beträgt die Ausfallrate 4 und die Skalierung 10, wodurch die meisten zufälligen Werte im Intervall [3.0, 15.0] generiert werden. Hier erfahren Sie mehr über die Weibull-Verteilung.
Mit den Optionen Rauschen R, Rauschen V, Rauschen V+T, Turbulenz V und Turbulenz V+T können Sie auf Grundlage eingegebener reeller Zahlen, Vektor- und/oder Uhrzeitdaten pseudozufällige Rauschwerte generieren. Der Parameter Skalierung definiert das Abhängigkeitsverhältnis zwischen Eingabe- und Ausgabedaten. Höhere Werte erzeugen gleichförmigeres Rauschen, niedrigere Werte abgehackte Rauschspitzen. Der Parameter Stärke bestimmt den Betrag der Ausgabewerte.
Die Turbulenzoptionen enthalten den Parameter Wiederholungen, der die Anzahl der Wiederholungen bzw. Oktaven zum Erzeugen des Fraktalrauschens festlegt. Weniger Wiederholungen führen zu einer gleichförmigeren Ausgabe. Der Parameter Wiederholungen hat einen Bereich von 1.0 bis 10.0. Die Rauschoptionen erzeugen positive und negative Werte; die Turbulenzoptionen generieren nur positive Werte.
In diesem Beispiel ( RandomTemplate07.max ) wird eine zufällige X-Koordinate eines Partikels zum Erzeugen zufälliger Rauschwerte für die Y-Koordinate verwendet:
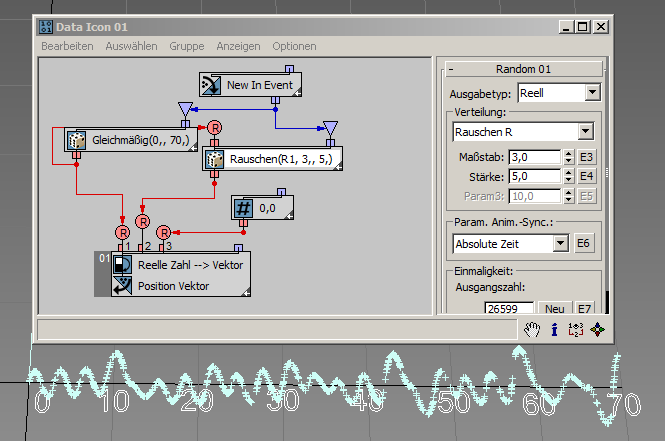
Im nächsten Beispiel ( RandomTemplate08.max ) sind die Partikel zufällig auf der Oberfläche des Datenoperatorsymbols angeordnet. Die Position dient dann als Eingabe für den Zufalls-Unteroperator mit der Option Rauschen V. Die Ausgabedaten werden zum Definieren der Partikelhöhen (Position der Z-Achse) verwendet.
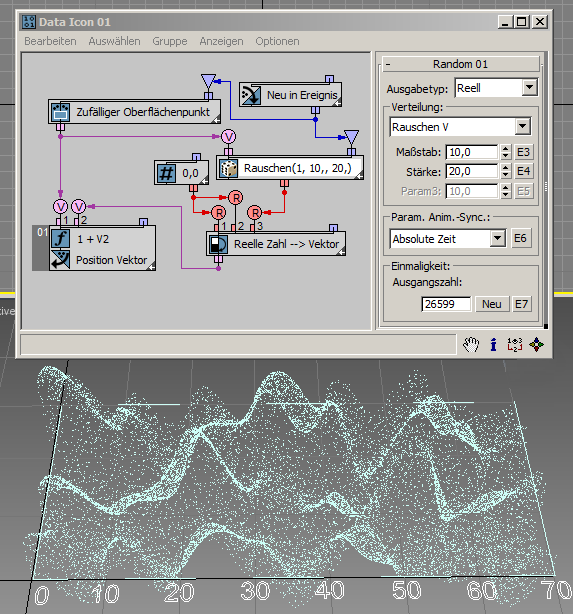
Durch Vernetzen der absoluten Zeit mit der Zeiteingabe der +T-Optionen kann das erzeugte Rauschen einfach animiert werden, wie in diesem Beispiel gezeigt ( RandomTemplate09.max ):
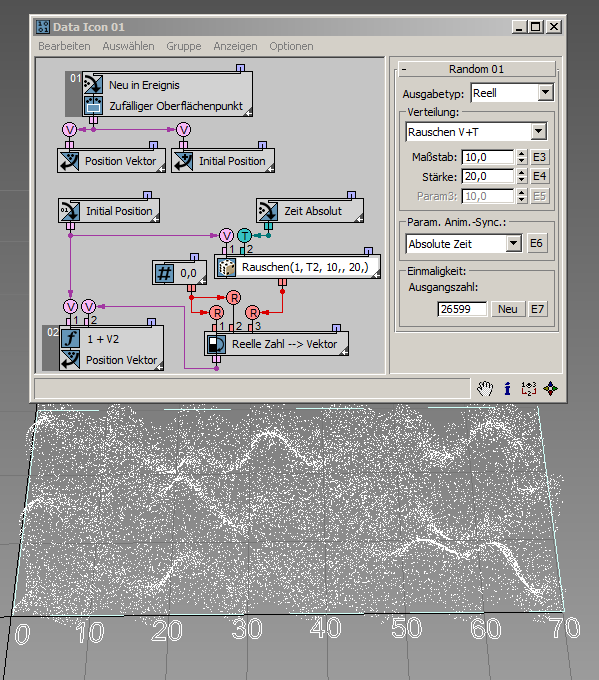
Die Turbulenzoptionen sind vergleichbar mit den Rauschoptionen. Sie müssen lediglich den Parameter Wiederholungen definieren, wie in diesem Beispiel gezeigt ( RandomTemplate10.max ).
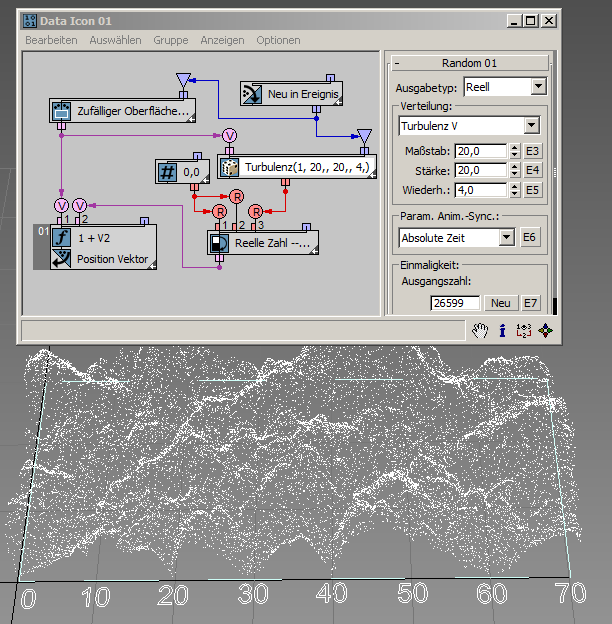
... und in diesem Beispiel ( RandomTemplate11.max ):
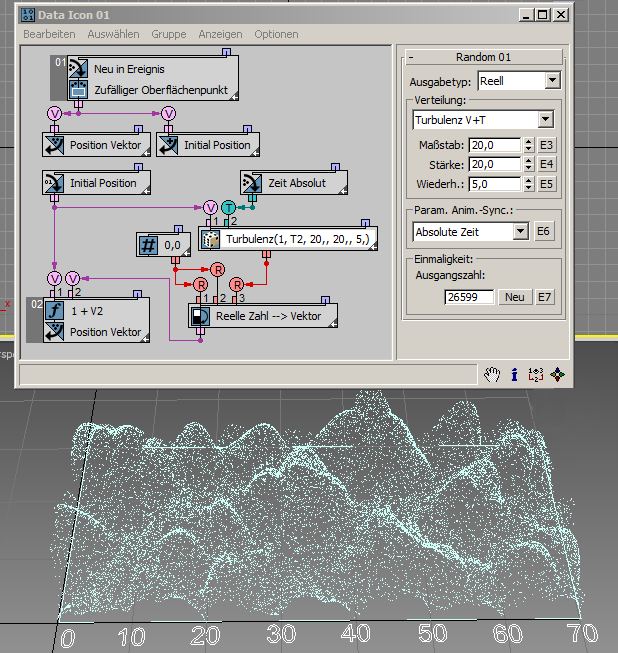
Die letzte Kategorie der Verteilungsoptionen gibt Vektordaten aus.
Die Gleichverteilung generiert zufällige Vektorwerte in einem Begrenzungsrahmen mit den Beschränkungen [–Max X, Max X] für die X-Komponente, [–Max Y, Max Y] für die Y-Komponente und [–Max Z, Max Z] für die Z-Komponente. Bei einer ausreichenden Anzahl von Partikeln kann der Begrenzungsrahmen mit zufälligen Vektorpunkten ( RandomTemplate12.max ) gefüllt werden:
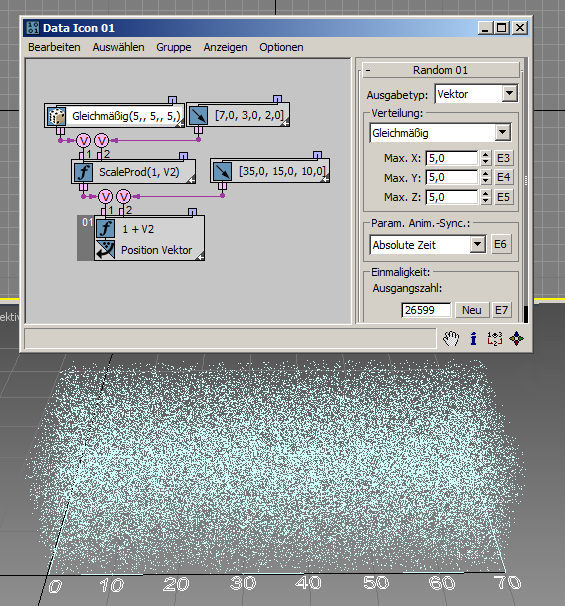
Die Option Kugeloberfläche kann verwendet werden, um Partikel auf der Oberfläche einer Kugel zu platzieren. Die am häufigsten verwendete Anwendung ist jedoch die Generierung eines Vektors mit zufälliger Richtung. In diesem Fall definiert der Parameter Radius die Länge des Vektors ( RandomTemplate13.max ):
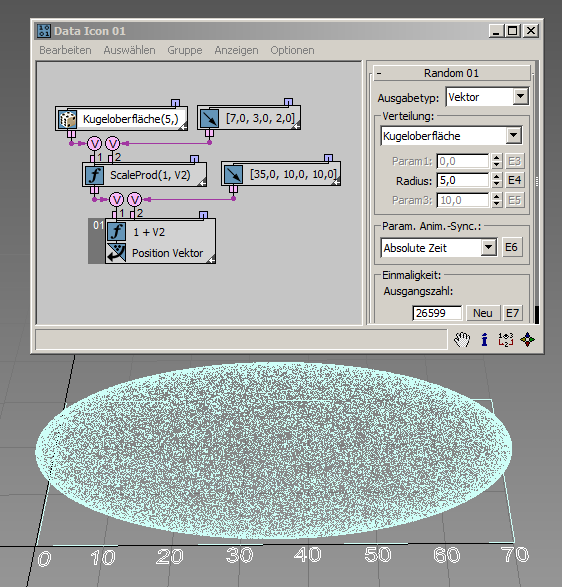
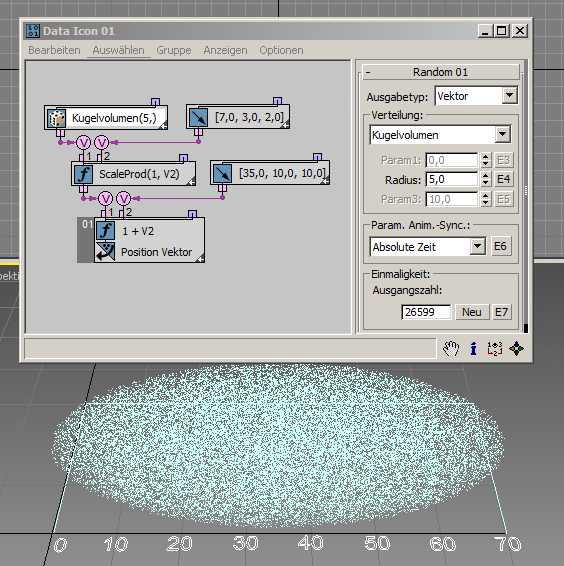
Sie können auch das gesamte Kugelvolumen mit zufälligen Punkten füllen ( RandomTemplate14.max ):
Sie können ein Kugelvolumen auch mit der Option Normal (Gauß) füllen, aber bei dieser Option besteht keine Begrenzung für die Kugel: In der Mitte der Kugel werden mehr und am Rand zunehmend weniger Punkte generiert. Die 3-Sigma-Regel von oben kann auch hier angewendet werden: 99,7 % der Punkte werden innerhalb einer Kugel mit einem Radius von 3*Sigma generiert ( RandomTemplate15.max ).
Die Optionen Rauschen R, Rauschen V, Rauschen V+T, Turbulenz V und Turbulenz V+T entsprechen den gleichnamigen Optionen für reelle Daten, mit der Ausnahme, dass sie Vektordaten generieren. Zur Veranschaulichung der Ausgabedaten können wir sie mit dem Geschwindigkeitskanal im Nach-Schritt verbinden und die Geschwindigkeit im Vor-Schritt auf null setzen. Auf diese Weise bleiben die Partikel bestehen und die Ausgabe kann als Geschwindigkeitslinie gezeichnet werden. In diesem Beispiel ( RandomTemplate16.max ) werden die Partikel zufällig in einem Rechteck platziert. Ihre Position wird dann als Eingabe für den Zufalls-Unteroperator mit der Option Rauschen V verwendet:
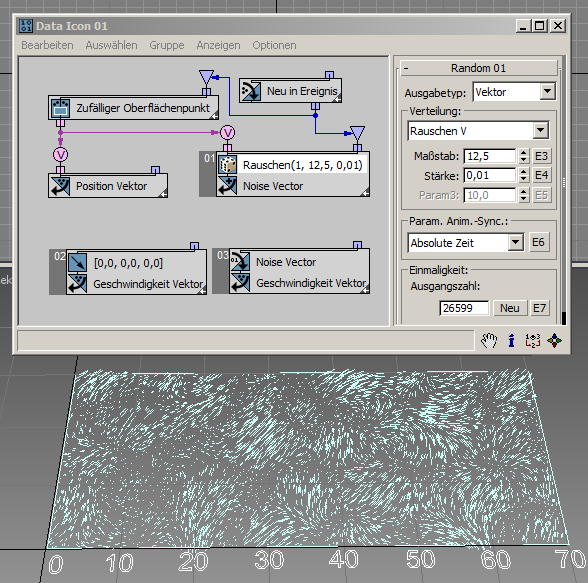
Dieses Beispiel ( RandomTemplate17.max ) zeigt dasselbe Szenario, allerdings mit der Option Rauschen V+T. Wir verwenden die aktuelle Uhrzeit als Eingabe für den Zufalls-Unteroperator, um die Animation des Rauschens zu erreichen:
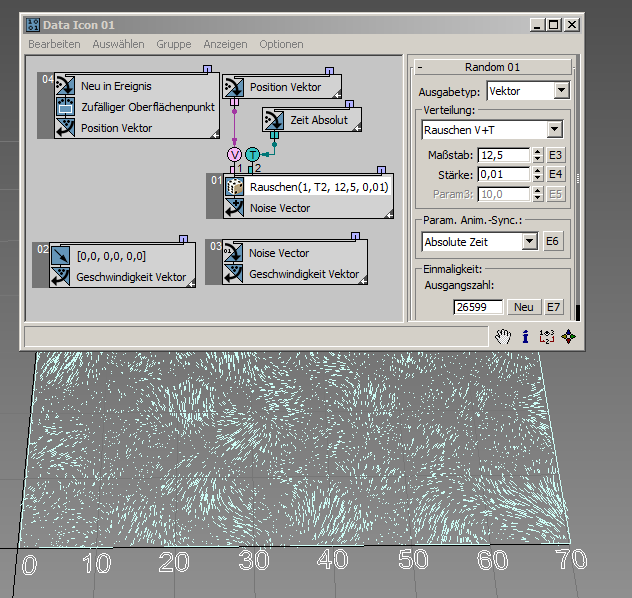
Wir können die Zufallsausgabe mit dem Geschwindigkeitskanal vernetzen und den Positionskanal als Eingabe für den Zufalls-Unteroperator verwenden, etwa zum Simulieren von Windturbulenzen. Das ist Frame 98 der Szenendatei RandomTemplate18.max :
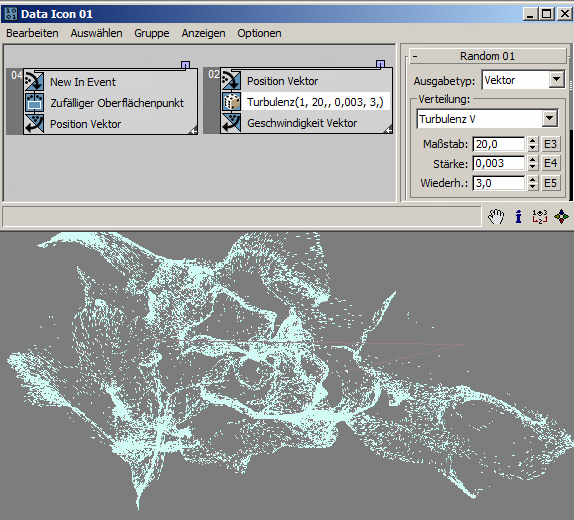
Benutzeroberfläche
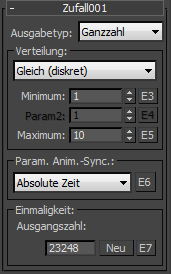
- Ausgabetyp
- Wählen Sie den Datentyp für die Ausgabe:
- Ganzzahl
- Reell
- Vektor
Die Einstellung Ausgabetyp legt die im Bereich Verteilung verfügbaren Werte fest.
Bereich Verteilung
Der Inhalt der Dropdown-Liste Verteilung hängt vom ausgewählten Ausgabetyp ab. Die Auswahl der Verteilung bestimmt wiederum die übrigen Parameter im Bereich Verteilung.
Detaillierte Informationen zu den Verteilungsoptionen und den zugehörigen Parameter finden Sie in den obenstehenden Erläuterungen.
- Parameter der Animationssync.
- Wenn Sie die Unteroperatorparameter animieren, kann die Software die Animation wahlweise auf alle Partikel ab dem Start-Frame der Animation bzw. dem ersten Frame des aktuellen Ereignisses oder auf der Grundlage des Partikelalters auf jedes Partikel anwenden. Folgende Optionen sind verfügbar:
- Absolute Zeit Keys für Parameter werden in den Frames angewendet, für die sie auch erstellt wurden.
- Ereignisdauer Keys für Parameter werden auf die Partikel relativ zu dem Frame angewendet, an dem sie erstmalig in das Ereignis eintreten.
- Partikelalter Keys für Parameter werden in den Frames angewendet, in denen die Partikel das entsprechende Alter erreicht haben.
- PartikellebensdauerSkaliert/Bildet die Animation der Parameter auf die Partikellebensdauer ab. Wenn beispielsweise ein Parameterwert aus 5–20 über die Frames 0 bis 100 animiert wird, hat dieser Parameter den Wert 5, wenn das Partikel erzeugt wurde, und den Wert 20, wenn das Partikel emittiert. Auf diese Weise können Sie z. B. die Änderung der Skalierung eines Partikels über seiner Lebensdauer hinweg definieren.
Damit diese Option ordnungsgemäß funktioniert, muss im Fluss ein Operator Löschen auf Nach Partikelalter gesetzt sein, um die Partikellebensdauer zu definieren.
- Zeitdateneingabe Fügt dem Unteroperator eine Zeiteingabe hinzu, die Sie mit einem beliebigen anderen Unteroperator, der Daten im Zeitformat ausgibt, verknüpfen können.
- E6
- Fügt eine Dateneingabe vom Typ Gleich hinzu, um den Animationssynchronisierungswert zu steuern. Diese kann nur Eingaben von einem Parameter-Unteroperator mit Typ = Animationssync empfangen.
- Einmaligkeit
- Mit dieser Option können Sie die vom Zufalls-Unteroperator generierte Reihenfolge der Zufallszahlen variieren. Geben Sie manuell einen Wert für die Ausgangszahl ein oder klicken Sie auf Neu, damit die Software eine Ausgangszahl generiert.
- E7
- Fügt eine Dateneingabe des Typs Gleich zur Steuerung der Einmaligkeit hinzu. Diese kann nur Eingaben von einem Parameter-Unteroperator mit Typ = Einmaligkeit empfangen.