Mit der Benutzeroberfläche "Kohäsives Material erstellen" können Sie ein kohäsives Material erstellen.
Jedes kohäsive Material, das von Simulation Composite Analysis verarbeitet wird, wird von Abaqus/Standard als benutzerdefiniertes Material betrachtet. Die Benutzeroberfläche "Kohäsives Material erstellen" bietet eine einfache Möglichkeit zum Erstellen dieser kohäsiven Materialdefinitionen in der Abaqus-Eingabedatei. Sie können das kohäsive Material, einschließlich der Schadensbeginn- und Schadensentwicklungsparameter, vollständig definieren. Beachten Sie, dass kohäsive Materialien in Simulation Composite Analysis nur zu Abaqus/Standard-Analysen kompatibel sind.
Um die Benutzeroberfläche "Kohäsives Material erstellen" aus Abaqus/CAE zu öffnen, gehen Sie zur Hauptwerkzeugleiste und wählen Sie . Die Benutzeroberfläche wird wie unten dargestellt angezeigt.
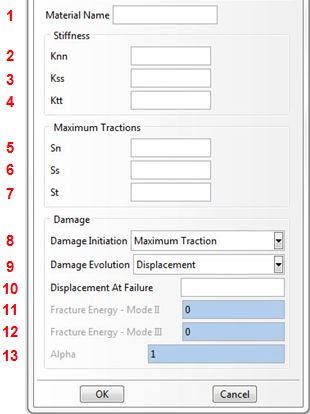
- Materialname – Geben Sie den Namen des gewünschten Materials ein. Dieser Name wird unter der Struktur "Materialien" in Abaqus/CAE angezeigt, nachdem das Material hinzugefügt wurde.
- Normale Steifheit – Zahl über null zur Definition der normalen Steifheit Knn des kohäsiven Materials. Knn setzt die normale Zugkraft im kohäsiven Material folgendermaßen zur Dehnung in Beziehung:
tn = Knnεn
wobei tn die normale Zugkraft und εN die Dehnung in Richtung der Normalen (lokale Richtung 3) ist.
- Steifheit bei erster Scherung – Zahl über null, die die Steiheit bei erster Scherung Kss des kohäsiven Materials definiert. Kss setzt die Zugkraft in der lokalen Richtung 1 im kohäsiven Material folgendermaßen zur Dehnung in Beziehung:
ts = Kssεs
wobei ts die Zugkraft bei erster Scherung und εs die Dehnung in der lokalen Richtung 1 ist. - Steifheit bei zweiter Scherung – Zahl über null, die die Zugkraft bei zweiter Scherung Ktt des kohäsiven Materials definiert. Ktt setzt die Zugkraft in der lokalen Richtung 2 im kohäsiven Material folgendermaßen zur Dehnung in Beziehung:
tt = Kttεt
wobei tt die Zugkraft bei zweiter Scherung und εT die Dehnung in der lokalen Richtung 2 ist. - Maximale normale Zugkraft – Zahl über null, die den maximalen Betrag der Zugkraft darstellt, die das kohäsive Material in normaler Richtung (lokale Richtung 3) aushalten kann, bevor der Schaden einsetzt, ausgedrückt als Sn.
- Maximale Zugkraft bei erster Scherung – Zahl über null, die den maximalen Betrag der Zugkraft darstellt, die das kohäsive Material in normaler Richtung (lokale Richtung 1) aushalten kann, bevor der Schaden einsetzt, ausgedrückt als Ss.
- Maximale Zugkraft bei zweiter Scherung – Zahl über null, die den maximalen Betrag der Zugkraft darstellt, die das kohäsive Material in normaler Richtung (lokale Richtung 2) aushalten kann, bevor der Schaden einsetzt, ausgedrückt als St.
- Kriterium des Schadensbeginns – Damit können Sie ein Schadensbeginnkriterium auf Basis der maximalen oder der quadratischen Zugkraft auswählen. Das Kriterium der maximalen Zugkraft definiert den Schadensbeginn als Zeitpunkt, zu dem beliebige Zugkräfte ihren entsprechenden Wert für maximale Zugkraft erreichen oder überschreiten. Das Kriterium auf quadratischer Basis verwendet eine quadratische Interaktion der Zugkraft zu maximalen Zugkraftverhältnissen, um den Schadensbeginn zu prognostizieren.
- Methode der Schadensentwicklung – Damit können Sie wählen, wie sich der Schaden nach Schadensbeginn entwickelt. Sobald der Schaden in einem kohäsiven Material einsetzt, wird die Steifheit des Materials verringert, während die Materialverformung zunimmt. Schließlich nimmt die Steifheit des kohäsiven Materials auf null ab, und das Material hält keiner Belastung mehr stand. Es stehen drei Methoden zur Verfügung:
-
Verschiebung
-
Energie
-
Energie (Gemischter Modus - Potenzgesetz)
-
- Variablenparameter – Die Wahl der Schadensentwicklungsmethode bestimmt die Eingabe für dieses Feld. Es stehen folgende Eingaben für die einzelnen Schadensentwicklungsmethoden zur Verfügung:
- Verschiebung – Dieser Wert ist die Verschiebung bei Ausfall, eine Zahl über null, die den Unterschied zwischen der effektiven Verschiebung und der effektiven Verschiebung bei Schadensbeginn definiert, ausgedrückt als
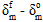 .
. - Energie – Dieser Wert ist die Bruchenergie, eine Zahl über null, die die gesamte, durch das Versagen abgeführte Energie definiert, ausgedrückt als Gc. In mathematischen Termen ist dieser Wert der Bereich unter der Zugkraft-Trenn-Kurve.
- Energie (Gemischter Modus - Potenzgesetz) – Dieser Wert ist die Bruchenergie im normalen Modus, eine Zahl über null, die die gesamte, durch das Versagen abgeführte Energie in einem reinen normalen Modus definiert, ausgedrückt als
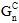 .
.
- Verschiebung – Dieser Wert ist die Verschiebung bei Ausfall, eine Zahl über null, die den Unterschied zwischen der effektiven Verschiebung und der effektiven Verschiebung bei Schadensbeginn definiert, ausgedrückt als
- Bruchenergie im ersten Schermodus – Zahl über null, die die gesamte, durch das Versagen abgeführte Energie in einem reinen ersten Schermodus definiert, ausgedrückt als
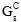 .
. - Bruchenergie im zweiten Schermodus – Zahl über null, die die gesamte, durch das Versagen abgeführte Energie in einem reinen zweiten Schermodus definiert, ausgedrückt als
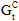 .
. - Alpha – Der Exponent, der in der Schadensentwicklungsgleichung im Mischmodus-Potenzgesetz verwendet wird, ausgedrückt als α.
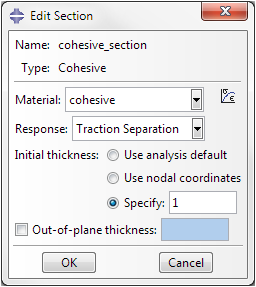
Zusätzlich zur Definition des Materials benötigen kohäsive Materialien in Simulation Composite Analysis einen kohäsiven Abschnitt, damit sie im Modell verwendet werden können. Der kohäsive Abschnitt kann wie jeder andere kohäsive Abschnitt in Abaqus erstellt werden. Wählen Sie im Modul "Abaqus/CAE Eigenschaft" die Option , um die Schnittstelle "Abschnitt erstellen" aufzurufen. Der kohäsive Abschnitt befindet sich unter der Kategorie Andere. Beim Bearbeiten des Abschnitts muss die Reaktion auf Zugkrafttrennung gesetzt werden (siehe Abbildung unten). Es ist auch erforderlich, die anfängliche Stärke auf einen Eins-Element-Wert (1) zu setzen. Dadurch wird sichergestellt, dass die Nominaldehnungen des kohäsiven Elements gleich den Verschiebungen sind; außerdem vereinfacht es die Definition der Eigenschaften des kohäsiven Materials.