(die energiebasierte Degradation ist nicht kompatibel mit gewebten Materialien)
Wenn der Wert der fünften Benutzermaterialkonstante 0 ist, wird die sofortige Degradation verwendet. Wenn der Wert 2 ist, wird die energiebasierte Degradation verwendet.
Sofortige Degradation
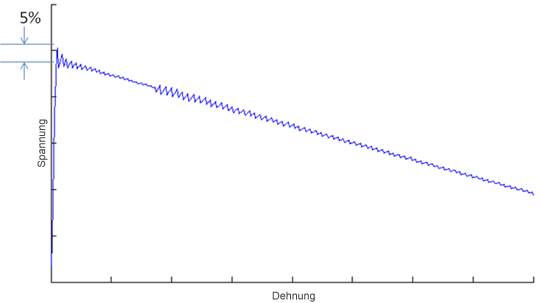
Die direkte Degradation ist die von Simulation Composite Analysis verwendete vorgabemäßige Schadensentwicklungsmethode. Wenn ein Schaden durch das Ausfallkriterium prognostiziert und die sofortige Degradation verwendet wird, wird die Steifheit der Faser und/oder Matrix sofort statt schrittweise auf den minimalen Wert reduziert. Der Umfang der Reduktion wird durch die Matrix- und Faserdegradationszahlen (BMK 12 und 13) gesteuert. Beachten Sie, dass bestimmte Ausfallkriterien, wie z. B. max. Spannung, nicht zwischen Matrix und Faser unterscheiden. Bei diesen Kriterien wird die Steifheit des Verbundwerkstoffs bei prognostiziertem Ausfall sofort reduziert, während ansonsten die Steifheiten von Matrix oder Faser unabhängig voneinander reduziert werden. Die Abbildung unten veranschaulicht die Wirkung einer sofortigen Steifheitsreduktion, wobei die Steifheit des Verbundwerkstoffs bei unterschiedlichen Schadenszuständen gezeigt wird. Die Steifheit des Verbundwerkstoffs bleibt konstant, bis der Matrixausfall auftritt, wodurch die Steifheit der Matrix auf einen bestimmten Anteilwert (BMK 12) der ursprünglichen Steifheit reduziert wird. Die Reduktion der Matrixsteifheit entspricht einer reduzierten Verbundwerkstoffsteifheit und diese Reduktion wird in einem einzigen Schritt angewendet. Wenn ein Faserausfall auftritt, wird die Steifheit entsprechend der BMK 13 reduziert und die Verbundwerkstoffsteifheit wird erneut entsprechend verringert.
Energiebasierte Degradation
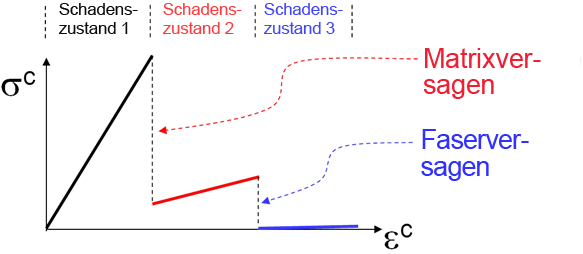
Die energiebasierte Degradation berücksichtigt die restlasttragende Funktion einer ausgefallenen Verbundlage, die in ein Verbundlaminat eingebettet ist. Wenn die energiebasierte Degradation aktiviert ist, reduziert Simulation Composite Analysis die Steifheit des Verbundwerkstoffs nach dem Auslösen eines Ausfallkritieriums schrittweise, anstatt die Verbundwerkstoffsteifheit sofort zu reduzieren. In diesem Fall identifiziert das Ausfallkriterium einfach den Beginn eines Ausfalls. Nachdem das Ausfallkriterium ausgelöst wurde, wird die Steifheit der Verbundwerkstoffkonstituente schrittweise über eine Reihe von einzelnen Steifheitsreduktionen reduziert. Diese Reduktionen werden angewendet, wenn der Dehnungszustand weiter über das Niveau bei Ausfallbeginn ansteigt. Wenn Sie diese Funktion verwenden, kann SDV1 zur Identifizierung des Fortschritts des Verbundwerkstoffschadens genutzt werden, wenn sich die Dehnung weiter erhöht. Eine ausführliche Beschreibung der energiebasierten Nichtlinearitätsfunktion finden Sie im Theoriehandbuch. Welche Steifheitsreduktionen jeweils erfolgen, hängt vollständig vom Ausfallzustand des Verbundwerkstoffs ab.
Matrixausfälle
Im Fall eines Matrixausfalls werden die Verbundwerkstoffe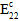 
, 
, 
, 
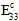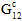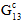und 
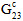linear degradiert unter Verwendung der Beziehung
wobei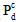 
die degradierte Verbundwerkstoffeigenschaft ist, 
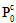die ursprüngliche Verbundwerkstoffeigenschaft und dm die Degradationskonstante aufgrund des Matrixausfalls angegeben durch
In der obigen Gleichung ist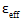 
ein für Verbundwerkstoffe effektives Dehnungsmaß angegeben durch
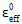ist der Wert für das effektive Dehnungsmaß von Verbundwerkstoffen bei Matrixausfall und 
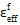ist der letzte effektive Dehnungswert angegeben durch
wobei Gm die gesamte vor und nach einem Matrixausfall im Verbundwerkstoff verbrauchte Energie ist (Benutzermaterialkonstanten 12).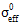 
ist die effektive Spannung des Verbundwerkstoffs bei Matrixausfall und wird auf die gleiche Weise berechnet wie die Gleichung A5.1. Le ist die repräsentative Elementlänge definiert durch Abaqus. Bei dreidimensionalen Elementen (z. B. Ziegel und Kontinuumschalen) ist die Länge des Elements die Kubikwurzel des Volumens. Bei zweidimensionalen Elementen (z. B. Schalen und Ebenenspannungselemente) ist die Länge des Elements die Quadratwurzel des Bereichs.
Die Definition der endgültigen effektiven Dehnung angegeben in der Gleichung A5.4 geht von einer linearen Degradation des Verhältnisses zwischen effektiver Spannung und effektiver Dehnung des Verbundwerkstoffs aus, wie unten gezeigt.
Um die MCT-Zerlegung zu erhalten und Spannungen in den Konstituenten nach einem Matrixausfall präzise zu erfassen, werden die Eigenschaften der Matrixkonstituente auch degradiert, um eine konsistente Beziehung von der Mikro- zur Makroskalierung zu erzwingen.
Faserausfälle
Ein Faserausfallereignis führt in ähnlicher Weise zu einer linearen Degradation der Verbundwerkstoffe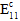 
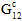, und 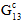wie zur Degradation der Verbundwerkstoffeigenschaften aufgrund eines Matrixausfalls, wobei die effektive Dehnung definiert wird als
und die effektive Spannung in ähnlicher Weise definiert wird. Die Längsscherdegradation wird jedoch angegeben durch
Dadurch wird erzwungen, dass die Schersteifheit die effektive Dehnung ausschließlich verringert.
Der Hauptunterschied zwischen Matrixausfällen und Faserausfällen ist der Bedarf an Konstituenteninformationen. Bei einem Faserausfall wird davon ausgegangen, dass die Matrix ebenfalls ausfällt, und es sind keine Konstituenteninformationen für weitere Ausfallberechnungen erforderlich. Daher werden die Konstituenteneigenschaften nach Faserausfällen nicht aktualisiert.
Die Bereitstellung der Abfuhrenergien für Matrix- und Faserausfallereignisse ermöglicht dem energiebasierten Degradationsschema die Berechnung der degradierten Verbundwerkstoff- und Konstituenteneigenschaften nach einem Ausfallereignis als Funktion der Erhöhung der Verbundwerkstoffdehnung. Die energiebasierte Degradation verringert die Netzabhängigkeit von einer endgültigen Lösung und bietet eine leistungsstarke progressive Schadensanalyse.
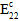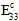, und 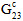entsprechend der Matrixdegradationsenergie degradiert. Andernfalls werden 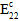, 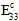und 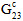entsprechend der Faserdegradationsenergie degradiert. Anmerkung zur diskreten Intervallunterteilung
Die energiebasierte Schadensfunktion von Simulation Composite Analysis verwendet mehrere diskrete Intervalle bei linearer Degradation des Verbundwerkstoffs, wie unten gezeigt. Jedes Intervall verwendet ein Sekantenmodul zum Definieren der Reaktion des Verbundwerkstoffs in diesem Intervall. Bei Problemen, in denen die Gesamtenergie in etwa einem gleichschenkligen Dreieck entspricht, erfassen die Intervalle genau die Reaktion des Verbundwerkstoffs.
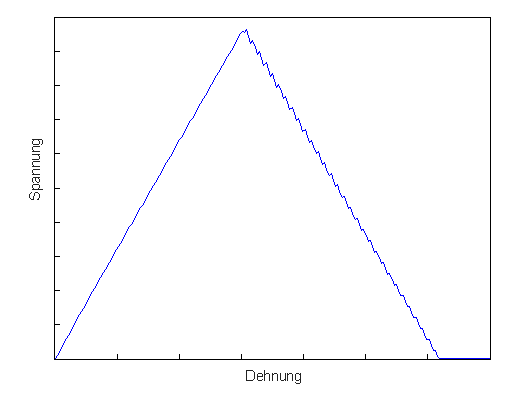
Bei Analysen, in denen die Gesamtenergie wie unten gezeigt einem stark verzerrten Dreieck entspricht, erfasst die Intervallunterteilung nicht genau die lineare Abschwächung des Verbundwerkstoffs in frühen Dehnungsebenen. Dies ist vollständig auf die Anzahl der Intervalle zurückzuführen, die für die schnelle und zuverlässige Behandlung des Problems verwendet werden. Besonders die Spannungssekantenintervalle bei Dehnungsgraden in Ausfallnähe behalten eine hohe Steifheit und können zu einer Fehlinterpretation des Spannungszustands des Verbundwerkstoffs führen. Wenn Sie bei einer Analyse eine lineare Degradationskurve definieren müssen, bei der die endgültige effektive Dehnung über 100 Mal über der anfänglichen effektiven Dehnung liegt, wenden Sie sich an den Autodesk-Support.
