Auswählen einer Kurve

Wenn Sie das Eingabediagramm verwenden, um Werte zu definieren, die sich während der Simulation ändern, stehen Ihnen verschiedene Optionen zum Definieren der Kurven sektoren zur Verfügung. Hierbei handelt es sich um Gesetze oder mathematische Funktionen, mit denen bestimmte Kurventypen erstellt werden.

Anmerkung: Wenn die Ausgaben in einer benutzerdefinierten Formel verwendet werden, wird ihr Browser-Name zusammen mit dem Namen des Eigentümers der Ausgabe in Klammern angehängt. Beispiel: "Kraft (Drehung:7)"

Auswählen mathematischer Funktionen und definieren ihrer Parameter

Definieren Sie die einzelnen Sektoren einer Kurve durch Zuweisen mathematischer Funktionen (d. h. Gesetze). Sie können mehrere aufeinander folgende Sektoren mit jeweils eigenen Gesetzen oder einer Verbindung aus verschiedenen Gesetzen erstellen, zum Beispiel eine Sinusfunktion kombiniert mit einer Neigungsfunktion. Sie können beispielsweise einen ersten Sektor mit einem kubischen Anstieg und einen zweiten Sektor mit einem Sinus erstellen. Die Software wendet das Kontinuitätsprinzip der globalen Gesetze an. Das kann zur Verwechslung des ersten Punkts des zweiten Sektors und des letzten Punkts des ersten Sektors führen, und andere Punkte können dadurch automatisch verschoben werden. Um die ursprünglich gewünschte Kurve zu erhalten, müssen Sie oft weitere Funktionen hinzufügen.

Nachdem Sie ein Gesetz ausgewählt und in das Feld Liste der Sektorgesetze verschoben haben, fügen Sie Parameter für das Gesetz hinzu. Führen Sie zum Hinzufügen von Parametern Folgendes durch:

Nachdem Sie einen Kurvensektor ausgewählt und die gewünschten Bedingungen hinzugefügt haben, können Sie den ausgewählten Kurvensektor definieren.

Klicken Sie im Feld mit der Liste der verfügbaren Gesetze auf den Abwärtspfeil, und wählen Sie das gewünschte Gesetz aus.
Klicken Sie auf , um das aktuelle Gesetz des Sektors durch das ausgewählte Gesetz aus der Liste zu ersetzen.
Sie können Gesetze beliebig oft auswählen und ersetzen, das im Feld mit den Gesetzen des ausgewählten Sektors angezeigte Gesetz wird jedoch durch das neue Gesetz überschrieben.

Sie können mehrere Gesetze auf denselben Sektor anwenden. Wenn Sie weitere Gesetze zu einem Sektor hinzufügen möchten, wiederholen Sie den ersten und diesen Schritt, klicken stattdessen jedoch auf . Wenn Sie ein Gesetz von einem Sektor entfernen möchten, der mehrere Gesetze enthält, wählen Sie das zu entfernende Gesetz im Feld Liste der Sektorgesetze aus, und klicken Sie auf .

Geben Sie die erforderlichen Eigenschaften für das im Feld Liste der Sektorgesetze angezeigte Gesetz ein.

Nehmen Sie für die jeweiligen Optionen folgende Einstellungen vor:

Geben Sie

Linearer Anstieg, Kubischer Anstieg, Zykloide, Harmonisch, Geänderter Sinus, Geändertes Trapez ein.

Die Koordinaten (X1, Y1) und (X2, Y2) der Punkte, die die Kurve definieren, ein, und/oder geben Sie einen Wert für Neigung ein, um die durchschnittliche Gradiente der Linie festzulegen. Die Kurve kann entweder durch Eingabe der Koordinaten der Start- und Endpunkte oder durch Eingabe der Koordinaten des Startpunkts sowie der durchschnittlichen Neigung des Sektors definiert werden.

Die Kurve verläuft symmetrisch über dem Mittelpunkt des Sektors.

Der Bereich unter der Kurve entspricht dem Bereich des Dreiecks unter dem entsprechenden linearen Anstieg.

Beim linearen Anstieg ist die Neigung konstant, d. h. die beiden Punkte des Sektors sind mit einer geraden Linie verbunden.

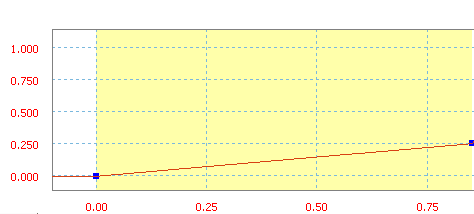
Linearer Anstieg mit einer Neigung von 30 Zoll/s.

Der kubische Anstieg ist durch ein Polynom dritter Ordnung definiert.

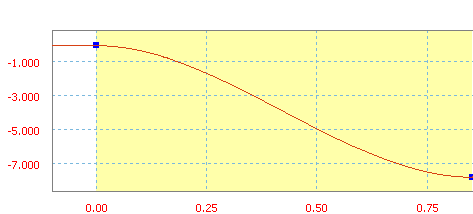
Kubischer Anstieg mit einer durchschnittlichen Neigung von 70 Zoll/s.

Eine Zykloide ist eine Rampenfunktion des Sinus/Kosinus.

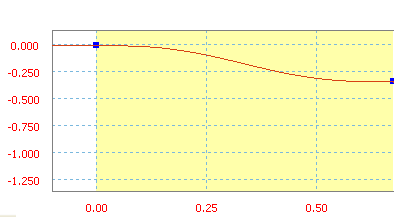
Zykloide mit einer durchschnittlichen Neigung von -50 Zoll/s.

Harmonisch ist eine Rampenfunktion des Sinus/Kosinus.

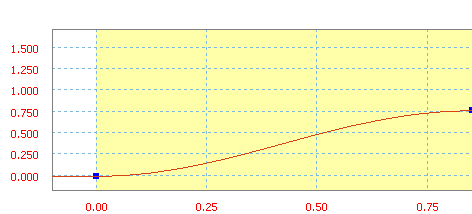
Harmonischer Anstieg mit einer durchschnittlichen Neigung von 90 Zoll/s.

Geänderter Sinus ist eine Rampenfunktion des Sinus/Kosinus.

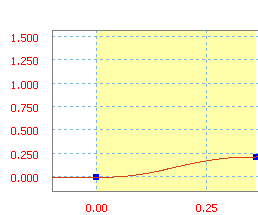
Geänderter Sinus mit einer durchschnittlichen Neigung von 60 Zoll/s.

Geändertes Trapez ist eine Rampenfunktion des Sinus/Kosinus.

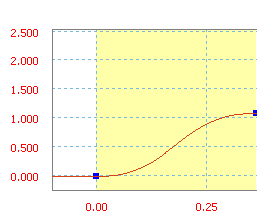
Geändertes Trapez mit einer durchschnittlichen Neigung von 300 Zoll/s.

Nehmen Sie für die jeweiligen Optionen folgende Einstellungen vor:	Eingabe
Sinus	ein Wert für Amplitude, um die Höhe der Kurve vom Zyklusmittelpunkt aus anzuzeigen, ein Wert für Frequenz, um die Anzahl der Zyklen pro X-Achseneinheit anzuzeigen, und für Phase, um den Abstand vom Zyklusstart zum Sektorbeginn anzuzeigen. Der Sinus ist eine klassische Funktion. Die Einheiten der Amplitude entsprechen der gesteuerten Variable (festgelegte Bewegung, Kraft). Die Einheiten der Frequenz entsprechen der Umkehrung der für die X-Achse verwendeten Variablen (bei Zeit in Hz). Die Phase wird in Grad oder als Bogenmaß angegeben.
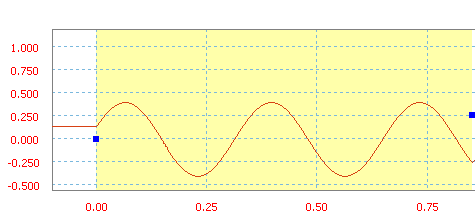
Sinus mit einer Amplitude von 40, einer Frequenz von 3 Hz und einer Phase von 20 Grad.
Polynom	Ein Polynom ist eine Polynomfunktion mit (in diesem Fall) bis zu 5 Graden. Die Koeffizienten des Polynoms können mit zwei Verfahren bestimmt werden. Methode 1 - Angeben der Koeffizientenwerte Geben Sie einen Wert für a0 und beliebig viele weitere a-Werte ein. Methode 2 - Importieren einer Textdatei öffnet das Dialogfeld Öffnen, mit dem Sie eine Datei zur Definition dieses Polynoms importieren können. Reihenfolge legt den Grad des Polynoms für die Kurve im ausgewählten Sektor fest. 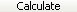berechnet den konstanten Wert und die Werte für die ersten fünf Grade dieses Polynoms. a0, a1, a2, a3, a4, a5 zeigt den konstanten Wert und die Wert für die ersten fünf Grade dieses Polynoms an. Diese Werte können bei Bedarf bearbeitet werden. Die Textdatei sollte wie folgt formatiert werden: //Kommentare - Kommentarzeilen sind optional und werden mit zwei Schrägstrichen eingeleitet. x1 y1 - Liste von Punkte mit x- und y-Werten. ... - eine Punktdefinition pro Zeile. xn yn - beliebig viele Punkte. Sie können die gewünschten Werte entweder manuell eingeben oder von der Software mithilfe der Interpolationsmethode der kleinsten Quadrate automatisch berechnen lassen.
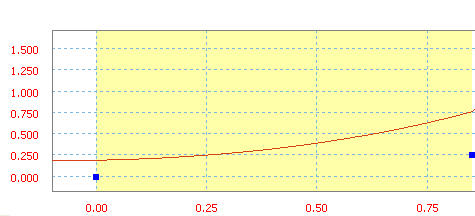
Polynom mit a0=20 in, a1=10 in/s, a2=50 in/s² und a3=20 in/s³.
Spline	Ein Wert für Neigung, um die Neigung der Linie festzulegen. Ein Spline ist eine kubische Funktion, die zur Interpolation zwischen aufeinander folgenden Punkten verwendet wird. Es gibt mehrere Möglichkeiten, einen Spline zu definieren. Dies sind: Sie können mühelos die Eingabepunkte mit der Maus im Diagrammbereich definieren, indem Sie doppelklicken bzw. mit der rechten Maustaste klicken und Punkt hinzufügen auswählen. Dieser Sektor wird von der Software jedoch als eine Reihe von Sektoren und nicht als einziger Kurvensektor behandelt. Genauere Koordinaten können Sie durch Importieren einer Textdatei eingeben. Mit Anfangsneigung wird die Neigung des ersten Punkts festgelegt. Mit Endneigung wird die Neigung des letzten Punkts festgelegt. Sie können einen bereits definierten Spline laden.
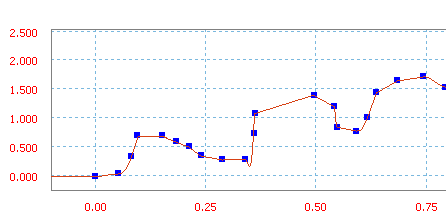
Durch Hinzufügen von Punkten definierter Spline.
Sie können den hier definierten Spline unabhängig von der Definitionsweise speichern. Anmerkung: Sie können keine weiteren Gesetze zu einem durch einen Spline definierten Sektor hinzufügen. Wenn Sie das Gesetz eines Sektors durch einen Spline ersetzen, werden zudem die Anfangs- und Endneigung automatisch von den vorherigen und nachfolgenden Sektoren übernommen, können jedoch zu einem späteren Zeitpunkt manuell geändert werden.
Wenn Sie eine Textdatei mit Tangentenpunkten verwenden möchten, strukturieren Sie die Datei folgendermaßen:
// Kommentare	Die Datei kann eine oder mehrere Kommentarzeilen enthalten. Jede Zeile muss mit "//" beginnen. Kommentarzeilen sind optional, bieten Ihnen jedoch die Möglichkeit, Hinweise zum Zweck des Splines anzugeben.
[Tangenten] T1 T2	Geben Sie den Wert der Tangente für die Anfangs- (T1) und Endpunkte (T2) des Sektors an. Diese Werte werden als "Anfangsneigung" und "Endneigung" auf der Benutzeroberfläche angezeigt. Wenn kein Wert angegeben wird, wird ein Tangentenwert von 0.0 (horizontale Tangente) impliziert. Diese Zeile ist ebenso wie Kommentarzeilen optional, allerdings müssen einige Werte vorausgesetzt werden, wenn kein Tangentenwert angegeben wird.
X₁ Y₁ ... X_n Y_n	Die Liste der Punktkoordinaten. Sie können beliebig viele Punkte aufführen. Geben Sie einen Punkt pro Zeile an.
Beispieltextdatei	// // Spline-Punkte für Simulationseingabe // Wert: Gelenkdrehmoment (N mm) // Referenz: Zeit (s) [Tangenten] -3.40775 -5.27803 +0.000 +0.000 +4.313 +1.510 +7.954 -9.756 +1.000 +0.000
Formel	Eine Formel im Feld Formel, um die Kurve zu definieren. Eine Formel ist eine Gleichung mit Funktionen und Schlüsselwörtern. Nur für die Definition des Gelenks und externer Kräfte verfügbar. Sie können für einen Freiheitsgrad keine Bewegung festlegen. Die Kontinuität mit angrenzenden Sektoren wird nicht automatisch beibehalten. Sie sollten sie definieren, um Kollisionen während der Simulation zu vermeiden. Formeln sind auf 255 Zeichen beschränkt. Sie können eine der folgenden Funktionen verwenden: abs fmod a cos cos log10 sqrt asin sinh log sqr atan sin pow trunk atan2 tanh sign pow10 floor cosh tan sign0 exp round
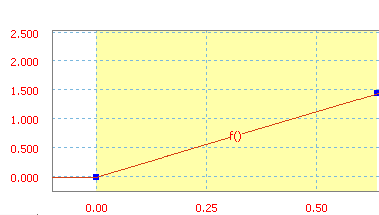
Durch die Formel Y = X + 37 definierte Kurve.

Beispiel 1

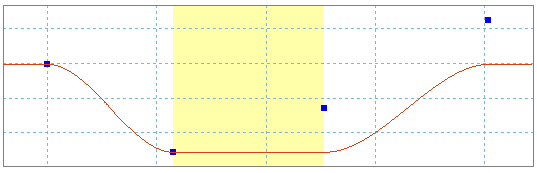
Sie erstellen drei Sektoren. In dem zweiten möchten Sie einen Niedrigfrequenz-Sinus.

Hier sehen Sie die Kurve vor und nach der Sinuserstellung. Der dritte Sektor wurde für die Kontinuität zwischen den beiden Sektoren vertikal verschoben. Um die ursprünglich gewünschte Kurve zu erhalten, müssen Sie weitere Funktionen hinzufügen.

Beispiel 2

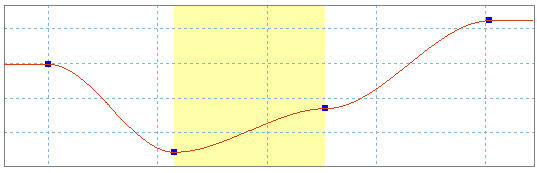
Einige Funktionen sind in ihren Definitionen eingeschränkt. Um einen Sinus zu erhalten, der um 300 herum variiert, müssen Sie ein Konstantengesetz mit dem Wert 300 und ein Sinusgesetz hinzufügen.

Anmerkung: Sie können die Gesetze in einer beliebigen Reihenfolge hinzufügen.

Die Variation um eine Nicht-Null-Neigung herum kann durch die Kombination einer Rampe mit einem Sinus modelliert werden.

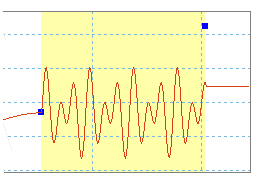
Beispiel 3

Um eine Vibration in einer Alternativbewegung zu simulieren, kombinieren Sie Sinusgesetze mit unterschiedlichen Amplituden und Frequenzen.

Definieren von Werten außerhalb eines Kurvensektors

Sie können auch Das Verhalten der Variablen außerhalb der Kurvensektoren, d. h. vor dem ersten und nach dem letzten Sektor, definieren. Nachdem Sie einen Bereich außerhalb der gesamten Kurve ausgewählt und die gewünschten Bedingungen hinzugefügt haben, können Sie den ausgewählten Bereich definieren.

Wählen Sie eine Definition für den außerhalb einer Kurve ausgewählten Bereich.
Wenn Sie Zyklisch auswählen, klicken Sie auf Start.
Hiermit wird das Dialogfeld zur Auswahl des Startpunkts geöffnet.
Klicken Sie im Dialogfeld Auswahl des Startpunkts auf den Abwärtspfeil rechts neben dem Feld.
Es wird ein Menü geöffnet, in dem jeder Punkt aufgeführt ist, mit dem ein Kurvensektor beginnt.
Klicken Sie auf den Punkt, mit dem der Kurvensektor beginnt, der für diesen Bereich kopiert werden soll.
Klicken Sie auf OK.

Sie haben fünf Möglichkeiten zur Definition des Bereichs außerhalb einer Kurve. Dies sind:

Konstanter Wert	Mit dieser Einstellung wird ein konstanter Wert festgelegt, der entweder dem ersten Wert in der Kurve entspricht, wenn Sie den Bereich links vom ersten Punkt definieren, oder dem letzten Wert in der Kurve, wenn Sie den Bereich rechts vom letzten Punkt definieren. Dies ist die Standardeinstellung.
Konstante Neigung	Mit dieser Einstellung wird eine Linie mit konstanter Neigung im ausgewählten Bereich definiert. Der Neigungswert entspricht entweder dem Neigungswert des ersten Kurvensektors, wenn Sie den Bereich links vom ersten Punkt definieren, oder dem Neigungswert des letzten Kurvensektors, wenn Sie den Bereich rechts vom letzten Punkt definieren.
Modulo	Mit dieser Einstellung wird entsprechend dem Moduloprinzip ein Wert im Definitionsbereich des Gesetzes festgelegt, wobei alle Sektoren definiert sind: eine definierte Kurve wird auf beiden Seiten der Ordinatenachsen wiederholt. Durch Dynamische Simulation wird geprüft, dass die Koordinate des letzten Punkts des Gesetzes (letzter Sektor) der Koordinate des ersten Punkts (erster Sektor) entspricht. Ist dies nicht der Fall, wird eine Fehlermeldung angezeigt, in der Sie zur Änderung der Werte aufgefordert werden. Diese Meldung wird angezeigt, weil Diskontinuitäten vom Berechnungsmodul nicht verarbeitet werden können. Dieser Modus wird auf den rechten und linken Teil des Gesetzes angewandt.
Zyklisch	Diese Funktion verwendet die Kopie eines Zyklus von einem benutzerdefinierten Punkt bis zum letzten Punkt der benutzerdefinierten Kurve. Wählen Sie als Startpunkt des Zyklus einen Punkt, der dem letzten Punkt der benutzerdefinierten Kurve entspricht. Anderenfalls besteht eine Diskontinuität zwischen dem Start und dem Ende des Zyklus. In diesem Fall wird eine Fehlermeldung angezeigt.
Frei	Mit dieser Einstellung wird keine Definition für diesen Bereich festgelegt. Es wird keine Kraft angewendet, und der (mit einer angewendeten Bewegung) angetriebene Freiheitsgrad wird freigesetzt. Für eine festgelegten Bewegung muss der rechte Sektor des letzten Punkts vor dem Freigeben des letzten Sektors freigegeben werden, dann der Sektor vor dem letzten usw.