This material model is available for 2D, brick, and tetrahedral elements. The Arruda-Boyce material model is a hyperelastic material model used to model rubber materials. The implementation of Arruda-Boyce follows the Ogden material behavior for volume-preserving deformation modes. The Arruda-Boyce material properties are listed below. In addition to these properties, it may be necessary to define some Isotropic Material Properties.
Click the Curve Fit button on the Element Material Specification dialog to use the Curve Fitting routine. This routine calculates the material constants using measured stress-strain data.
The potential function of the material is as follows:
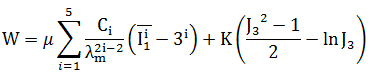
where C1= 1/2, C2= 1/20, C3= 11/1050, C4= 19/7000, and C5= 519/673750.
Since this model was developed starting out from a representative volume element where eight springs emanate from the center of a cube to its corners, it is known as the eight-chain model.
The potential depends on the first invariant only. The physical interpretation is that the eight chains are stretched equally under the action of a general deformation state. The first invariant directly represents this elongation.
Mu
Mu (μ ) is a constant that is related to the consistent shear modulus of elasticity (μ 0 ) as follows:
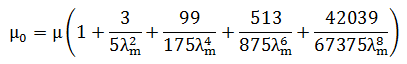
Locking Stretch
The locking stretch (λm) is the stretch at which the stress goes to infinity because the polymer network chains are fully extended and rigid. The slope of the stress-strain curve rises significantly at this approximate value of stretch. This value is normally calculated through the curve fitting algorithm.
K
K is a constant related to the bulk modulus of elasticity (K 0) as follows:
K 0 = 2K.