L’analyse Footfall est un type d’analyse de la structure permettant d’étudier l’influence des pas des piétons (interprétés comme une force harmonique dans un certain intervalle de fréquences) sur les vibrations de la structure.
L’analyse Footfall est applicable aux structures sans non-linéarités matérielles, géométriques et structurelles. Si une structure contient des barres élasto-plastiques, des appuis, des relâchements, des compatibilités non-linéaires ou unilatérales, des câbles, des éléments travaillant en traction ou compression seule, la définition de l’analyse Footfall ne sera pas possible.
L’analyse consiste à déterminer une réponse verticale (coefficient de réponse, accélération, vitesse, déplacement) dans les nœuds de la structure causée par une charge due à la force harmonique appliquée aux nœuds. La charge harmonique est variable dans le domaine fréquence (FRF) défini.
Il existe deux approches pour étudier les effets de l’analyse Footfall :
- On analyse la réponse dans le même nœud auquel est appliquée la force (simplifié - en anglais self excitation).
- On analyse la réponse dans un nœud quelconque pour l’influence de la force appliquée à un autre nœud (complet - en anglais full excitation).
On applique une force harmonique à chacun des nœuds sélectionnés de la structure en utilisant le mécanisme de l’analyse FRF avec prise en compte de l’amortissement. Vous pouvez définir la plage de fréquences pour la force d'excitation (par défaut, la plage de fréquences change en fonction de la méthode d'excitation sélectionnée). La plage de fréquences est divisée en 20 intervalles, avec la prise en compte des points supplémentaires pour les fréquences des modes de vibrations propres.
À la suite de l’analyse, on obtient les résultats nodaux. Le résultat le plus important de l’analyse est le coefficient de réponse qui indique combien de fois les vibrations calculées dépassent les vibrations admissibles ressenties par l’homme.
Une fois l’analyse effectuée, les résultats dans les nœuds sont disponibles :
- Sous forme de tableau de nœuds (Résultats / Avancés / Analyse footfall - Tableaux)
- Sous forme de cartographies sur panneaux et barres (Résultats / Avancés / Analyse footfall - Cartographies)
- Sous forme de diagrammes (Résultats / Avancés / Analyse footfall - Diagrammes)
Le coefficient de réponse est déterminé à la suite de deux types d’analyse différents :
- L'analyse harmonique
- L'analyse de réponse temporelle impulsive
Le critère pour la sélection du type d’analyse est la première fréquence principale de modes propres et la fréquence maximale du mouvement piéton.
Forces d'excitation en fonction du Concrete centre (2006)
Analyse harmonique
L’analyse harmonique consiste à décomposer les fonctions de vibrations en séries de Fourier (composantes harmoniques). On utilise jusqu’à quatre composantes de la série. La valeur maximale multipliée quatre fois de la plage de fréquence du mouvement piéton est normalement de 8 à 10 Hz. Si la fréquence de base des vibrations propres est inférieure à cette valeur, on peut en déduire l'intervalle de l’excitation. On calcule l'accélération pour chacun des 4 composants harmoniques à chaque pallier de l'intervalle de la fréquence d'excitation. Ensuite, on calcule le coefficient de réponse pour chacune des composantes harmoniques en comparant l’accélération obtenue à l’accélération de base aR=1 (m/s2) :
Pour f h < 4 Hz
Pour 4 Hz < fh < 8 Hz
a R=1,h = 0.0071
Pour f h > 8 Hz
Le coefficient de réponse pour la composante harmonique h :
On obtient le coefficient total de réponse en analyse harmonique en calculant la racine de la somme des carrés de quatre coefficients de réponse pour les composantes harmoniques.
Analyse de réponse temporelle
Si une structure est plus rigide et sa fréquence de vibrations propres est supérieure à 10 Hz, le risque de vibrations résonantes est réduit. Chaque pas d’un piéton provoque des vibrations par l’excitation simple disparaissant avec le temps. Il suffit d’effectuer l’analyse temporelle pour une impulsion simple provoquée pour la fréquence maximale de l’intervalle du mouvement piéton. En résultats, on obtient l’allure de la fonction de vitesse dans le temps. La mesure des vibrations est la valeur moyenne de la fonction temporelle de vitesse, vitesse root mean square :
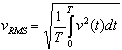
Le coefficient de réponse pour l’analyse temporelle est calculé comme
Rf = v RMS / vR=1
où la vitesse de base v R=1 (m/s) est :
V R=1 = 5.0 * 10-3 /2 π f1 pour la fréquence de vibration de base f 1 < 8 Hz
v R=1 = 1.0 * 10 -4 pour f 1 ≥ 8 Hz.
Pour une structure dont la fréquence des vibrations fondamentales égale environ 8-10 Hz, l’influence des vibrations résonantes et par impulsions peut avoir lieu. Le programme effectue les deux types d’analyses des vibrations et retient, comme coefficient total de vibrations, le plus élevé obtenu à l'issue des deux types d’analyse.
Forces d'excitation en fonction de SCI P354:Design of Floors for Vibration
Le coefficient de réponse pour l’analyse aussi bien harmonique que temporelle est calculé à partir de l’accélération moyenne RMS pondérée par la fréquence a w,rms.
Calcul du coefficient de réponse :
R f = a RMS / aR=1
où : l’accélération de base aR=1 (m/s2), pour les vibrations verticales, par rapport à l’axe Z, d’après BS 6472 et ISO 10137, est égale à :
a R=1 = 5*10-3
Forces d'excitation selon AISC DG11: Floor Vibrations due to Human Activity
L'analyse est effectuée uniquement en condition de vibrations à résonance permanente. Il n'existe pas de résultats des vibrations non permanentes avec cette méthode.
Le facteur réponse est calculé sur la base de l'accélération maximale par rapport à l'accélération gravitationnelle g.
R f = a p / g
L'accélération admissible selon AISC DG11 Table 4.1 a 0 / g est :
- Pour les bâtiments de bureaux, d'appartements et les églises 0,005 (0,5 %)
- Pour les zones commerciales 0,015 (1,5 %)
Références :
- A Design Guide for Footfall Induced Vibration of Structures, M.R. Willford, P.Young, The Concrete Center 2006
- SCI P354: Design of Floors for Vibration: A New Approach The Steel Construction Institute (2007 Edition)
- Steel Design Guide Series 11, Floor Vibrations Due to Human Activity, AISC 2003