L'algorithme de calcul des flèches des dalles BA consiste à utiliser les calculs de la dalle isotrope élastique faite en matériau élastique, pour lesquels on prend ensuite en compte les changements de la rigidité du matériau due à la fissuration. Les déplacements primaires sont calculés par le biais de la Méthode des éléments finis (MEF). Ensuite, ils sont modifiés.
Les calculs sont effectués séparément pour chaque panneau. Ce principe est correct si le panneau peut être identifié avec un élément de structure (panneau, segment du plancher). Dans le cas contraire, les valeurs de la rigidité mises en moyenne dans le cadre du panneau peuvent être perturbées. Cette situation peut entraîner l'influence d'éléments très éloignés sur les déplacements de l'EF analysé. L'influence de ce type de perturbations sur les valeurs extrêmes n'est pas très importante, pourtant les cartographies des déformations (flèches) doivent être considérées avec prudence.
Il est recommandé que chaque segment du plancher dans lequel les extrêmes locaux des flèches peuvent se produire soit modélisé en tant qu'un panneau séparé. Le panneau doit être défini dans les limites des appuis qui l'entourent (de même que les travées sont limitées par les appuis en cas de poutres), mais pour le panneau, ces appuis ne doivent pas être continus sur tout le contour du panneau.
La division en panneaux n'influence pas les résultats de la vérification par la méthode Avec mise à jour de la rigidité (MEF), si l'on admet que les charges, la géométrie et les armatures calculées sont identiques.
Les calculs sont effectués pour la combinaison sélectionnée (séparément pour les déplacements inférieur et supérieur) ou pour le groupe de combinaisons, si cela est exigé par la norme (combinaisons fréquentes, rares ou quasi-permanentes). La combinaison sélectionnée pour les calculs est celle pour laquelle les déplacements élastiques maximaux (séparément positifs et négatifs) ont lieu. Si le panneau ne peut pas être traité comme élément de structure (il contient d'autres éléments), les cartographies des déformations (flèches) doivent être considérées avec prudence. Toutefois, cela n'influence pas beaucoup les valeurs extrêmes des flèches pour un panneau donné.
L'attention est attirée sur les déplacements des autres appuis dans les coins de la dalle.
L'algorithme de calcul utilisé dans Robot est basé sur le principe que les flèches totales (réelles) d'une dalle BA sont égales au produit de ses flèches élastiques et du coefficient de rigidité D / B.
où :
- les déplacements réels du enième point de calcul de la dalle prenant en compte la fissuration et les armatures calculées
- les déplacements élastiques du enième point de calcul de la dalle
D - la rigidité de la dalle pour rigidité du matériau admise (comme dans les calculs MEF)
B - la rigidité équivalente d'une dalle BA, calculée avec la prise en compte de la fissuration de l'élément, des effets rhéologiques, de l'adhérence des armatures calculées, etc. mise en moyenne pour les deux directions.
En pratique, une telle approche est limitée à une mise à l'échelle linéaire des déplacements élastiques spécifiques par le coefficient global de chute de la rigidité.
L'algorithme des calculs pour la méthode de rigidité équivalente (élastique) est le suivant :
Après l'analyse de la structure à l'aide de la MEF et les calculs de la quantité de ferraillage théorique pour l'ELU, l'ELS (en ce qui concerne les calculs de la fissuration, des limites des contraintes, ou les problèmes qui peuvent être envisagés localement) et l'ACC, le logiciel calcule les rigidités pour chaque élément fini (EF). Les calculs de la rigidité sont effectués pour les deux directions des armatures. L'étendue et la méthode de calcul de ces rigidités dépendent des exigences détaillées d'une norme donnée. A la suite des calculs, deux valeurs de la rigidité sont obtenues (dans la plupart des cas différentes) pour chaque élément fini. Pour les calculs ultérieurs, la moyenne pondérée des rigidités composantes est utilisée. Le poids de la mise en moyenne est le rapport des moments agissant sur un élément donné dans les deux directions.
où :
Bx, By - les rigidités réelles calculées pour deux directions du ferraillage
cf - le coefficient de poids calculé d'après la formule :
- si | Mxx | / | Myy | > 4, alors cf = 1
- si 0,25 ≤ | Mxx | / | Myy | ≤ 4, alors
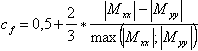
- si | Mxx | / | Myy | < 0.25, alors cf = 0.
Grâce à ces formules, dans le cas d'une disproportion importante des moments (la proportion du moment plus important par rapport au moment plus faible est supérieure ou égale à 4.0 - par exemple les dalles fléchies dans un plan), c'est la rigidité de la direction où agit le moment plus important qui est prise en compte. Par contre, si les valeurs des moments sont similaires, la rigidité de la direction donnée est affectée proportionnellement au rapport des moments.
L'étape suivante des calculs consiste à calculer la relation de la rigidité élastique par rapport à la moyenne pondérée des rigidités réelles, calculée de la manière présentée ci-dessus. Ce calcul est effectué pour chaque élément fini :
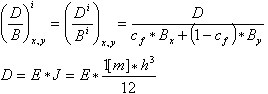
Le coefficient de dalle (1 - n*n) est pris en compte dans les calculs de la rigidité B et D.
Les valeurs des rigidités réelles obtenues dans les calculs peuvent être suivies par l'activation des cartographies de Coefficient de rigidité.
Si les propriétés des matériaux utilisés au cours de la conception sont identiques à ceux utilisés dans un modèle, la valeur du coefficient D /B > 1,0. Ce dernier peut être interprété (principalement pour les dalles soumises à une flexion unidirectionnelle) en tant que multiplicateur de flexion. Si plusieurs matériaux sont utilisés dans un modèle et des calculs (par exemple, avec différentes classes comme des bétons dont les modules de Young ou les coefficients de Poisson diffèrent), la valeur du coefficient est corrigée automatiquement. Il est alors possible que l'inéquation mentionnée ci-dessus soit perturbée.
L'étape suivante consiste à calculer la moyenne à partir des rapports de rigidités calculés précédemment. Le rapport global final de rigidités, utilisé pour calculer les déplacements réels de la dalle (c'est-à-dire la mise à l'échelle linéaire des déplacements élastiques), est le nombre obtenu à partir de la prise de la moyenne des rapports de rigidités (à poids égal à 0,25) et du rapport des rigidités enregistré pour l'élément sur lequel l'extrême du moment de flexion agissant dans une direction quelconque est présent (à poids égal à 0,75).
L'algorithme de la méthode de rigidité équivalente (élastique) présume le moyennage de la rigidité pour tous les éléments finis ; la forme de la ligne de flexion est, par conséquent, identique à la ligne de flexion multipliée par le coefficient de rigidité.
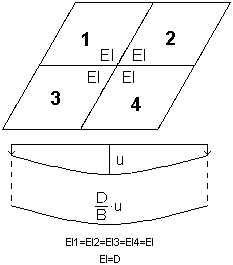
L'algorithme de la méthode avec mise à jour de la rigidité (non élastique) est identique à l'algorithme de la méthode de rigidité équivalente (élastique) jusqu'au moment où la rigidité calculée (différente pour la direction X et pour la direction Y).est affectée indépendamment pour chaque élément fini. Une dalle anisotrope de rigidité variable est alors obtenue. Pour les rigidités ainsi admises, le programme calcule la flèche de la dalle.
Dans la méthode avec mise à jour de la rigidité, chaque élément fini possède une rigidité déterminée séparément, alors les lignes de flexion peuvent différer. Pour chaque élément fini, on obtient une autre rigidité pour chaque direction.
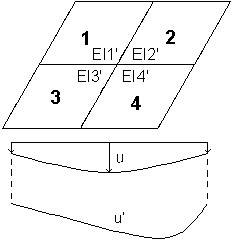
Si l'option Correction du ferraillage sur l'onglet Paramètres ELS dans la boîte de dialogue Type de ferraillage de plaques et coques est activée, pendant les calculs le logiciel augmente la section d'acier pour augmenter la rigidité de l'élément ce qui, par conséquent, permet de limiter les flèches de la plaque.
Les armatures sont réparties dans les deux directions en proportion inverse à la rigidité. Si la limitation des flèches au-dessus de la valeur admissible définie par l'utilisateur n'est pas possible (la correction du ferraillage pour la section d'acier admissible n'est pas possible), après la fin des calculs de la section d'acier théorique, l'avertissement suivant s'affiche : ‘La flèche admissible pour le panneau n° a été dépassée'.
Dans le logiciel, aucune limitation concernant le ferraillage outre celle résultant de la norme n'est définie, par conséquent, vous devez faire attention aux aspects économiques de la solution obtenue et au fait que plus la flèche diffère de celle exigée, moins la méthode utilisée est efficace.