La liste déroulante comprend les types suivants de géométrie des dalles ainsi que leurs paramètres :
|
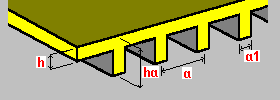
Raidisseurs d'un côté dans une direction : h - épaisseur de la dalle ha - hauteur des raidisseurs a - espacement des raidisseurs a1 - largeur des raidisseurs. |
|
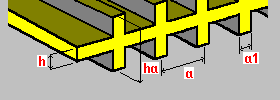
Raidisseurs de deux côtés dans une direction : h - épaisseur de la dalle ha - hauteur des raidisseurs a - espacement des raidisseurs a1 - largeur des raidisseurs. |
|
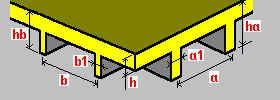
Raidisseurs de deux côtés dans deux directions : h - épaisseur de la dalle ha - hauteur des raidisseurs hb - hauteur des raidisseurs a - espacement des raidisseurs a1 - largeur des raidisseurs. b - espacement des raidisseurs b1 - largeur des raidisseurs. |
|
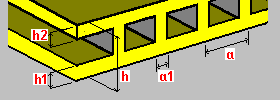
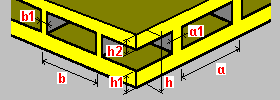
Plancher alvéolaire à raidisseurs dans une direction : h - épaisseur du plancher h1 - épaisseur de la plaque supérieure h2 - épaisseur de la plaque inférieure a - espacement des raidisseurs a1 - largeur des raidisseurs. |
|
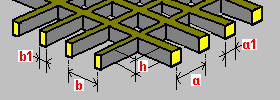
Plancher alvéolaire à raidisseurs dans deux directions : h - épaisseur du plancher h1 - épaisseur de la plaque supérieure h2 - épaisseur de la plaque inférieure a - espacement des raidisseurs a1 - largeur des raidisseurs. b - espacement des raidisseurs b1 - largeur des raidisseurs. |
|
Radier partiel : h - hauteur des raidisseurs a - espacement des raidisseurs a1 - largeur des raidisseurs. b - espacement des raidisseurs b1 - largeur des raidisseurs. |
|
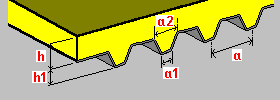
Bandeaux sur bacs acier : h - épaisseur de la dalle h1 - hauteur du bac acier a - espacement des nervures du bac acier a1 - largeur inférieure des nervures a2 - largeur supérieure des nervures |
|
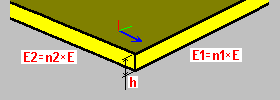
Orthotropie du matériau : h - épaisseur de la dalle n1 - coefficient de rigidité n2 - coefficient de rigidité. |
|
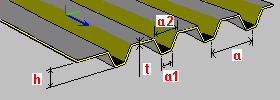
Tôle trapézoïdale : h hauteur de la tôle t épaisseur de la tôle a, a1, a2 – dimensions d’un segment de la tôle (espacement, épaisseurs) |
|
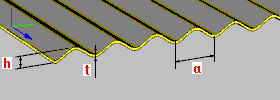
Tôle ondulée : h hauteur de la tôle t épaisseur de la tôle a – dimensions d’un segment de la tôle (espacement) |
|
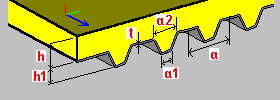
Dalle composée avec tôle trapézoïdale h - épaisseur de la dalle h1 - hauteur de la plaque t épaisseur de la tôle a, a1, a2 - dimensions d’un simple module de la tôle (espacement, largeurs) Es - module de Young (acier trapézoïdale) vs - coefficient de Poisson (acier trapézoïdale) Eb - module de Young (béton ; valeur adoptée sur la base du matériau sélectionné) vb - coefficient de Poisson (béton ; valeur adoptée sur la base du matériau sélectionné) |
|
Epaisseur constante avec rigidité réduite : h - épaisseur de la dalle Coefficients de réduction des éléments de la matrice : rigidité de la membrane D, rigidité pour la flexion K et rigidité pour le cisaillement H ; en outre, il est possible de définir un coefficient de réduction du poids pris en compte lors de la génération d'une charge à poids propre ; les valeurs de ces coefficients sont définis dans la boîte de dialogue Coefficients de rigidité, poids, masse qui s'ouvre après un clic sur Coefficients. |
|
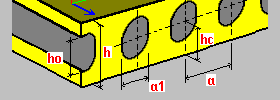
Plancher alvéolaire (avec ouvertures circulaires ou ovales) h - épaisseur de la dalle a - espacement des raidisseurs, espacement des ouvertures a1 - largeur de l'ouverture / diamètre du cercle ho - hauteur de l'ouverture (dalle avec ouvertures ovales) hc - distance entre le centre de l'ouverture et le bord de dalle h1 - hauteur de l'aile inférieure de la dalle h2 - hauteur de l'aile supérieure de la dalle (h2 = h - hc - c/2 - a1/2) c = ho - a1 (dalle avec ouvertures ovales) L'option Négliger la rigidité de flexion transversale permet d'ignorer ou de prendre en compte la rigidité K_YYYY dans les calculs. La non prise en compte de la rigidité de flexion (direction Y) vise à améliorer la modélisation des planchers alvéolaires préfabriqués. |
L'orthotropie de matériau introduit une rigidité différenciée pour les deux directions de la dalle, cela est dû aux différentes propriétés physiques dans les directions perpendiculaires. La différence de rigidité est déterminée à l'aide des modules de Young modifiés E1, E2 relatifs aux directions x, y de l'orthotropie, respectivement. Les modules E1, E2 sont le produit du matériau sélectionné et des coefficients n1, n2 définis par l'utilisateur. Le coefficient de Poisson est constant pour les deux directions. L'orthotropie de ce type peut être utilisée, par exemple, pour la modélisation des dalles BA ferraillées dans les deux directions.
Le coefficient de rigidité des plaques BA ferraillées dans deux directions est défini au moyen de la formule ci-dessous. Si on admet que le matériau de la plaque est élastique de façon linéaire, le coefficient de rigidité pour la direction parallèle à la direction du ferraillage est égal à :
n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)
où :
h – hauteur de la section de la dalle
m = Ez/Eb est le rapport du module de Young pour l’acier et le béton.
e – distance du centre de gravité du ferraillage du plan central de la dalle
u – ratio acier/béton (exprimé en fraction décimale), c'est-à-dire l'aire de la section d'acier par rapport à l'aire de la section de la plaque.
Rubrique connexe :