Remarques préliminaires :
Dans la majeure partie des cas, l’origine des charges est la force de gravitation (masse). Le calcul dynamique impose donc que ces masses soient prises en compte. Pour permettre à l’utilisateur une conversion facile des charges statiques (gravitationnelles) en masses, la commande spéciale « MASses ACTivées » à été introduite dans l’analyseur des fichiers texte.
La définition de la conversion est également possible dans la boîte de dialogue Options de calcul. Cela permet à l’utilisateur de définir les charges en vue de l’analyse statique et, ensuite, de les utiliser pour créer la répartition des masses dans le modèle de calcul de la structure en vue de l’analyse dynamique.
Pour que la conversion soit effectuée de façon correcte, la commande exige deux paramètres. Le premier composant est le jeu de directions pour lesquelles les masses seront actives. Normalement toutes les directions du repère global (X, Y, Z) sont utilisées car l’inertie n’agit pas en toutes les directions, mais seulement dans le cas des calculs spéciaux. Le deuxième paramètre est la valeur de l’inertie définie par le numéro du cas de charge statique et par la direction des charges à prendre en compte lors de la conversion. De plus, on peut donner le coefficient multiplicateur de la valeur de la charge.
Le caractère de la charge est automatiquement converti en masses : les forces ponctuelles sont transformées en masses ponctuelles, les moments en inertie de rotation, et les forces réparties en masses continues.
Syntaxe :
ANA [ DYN | MODes | TEMPorelle | HARmonique | SISmique | SPEctrale ] (concerne tous les types d'analyse dynamiques)
CASe (#<numéro> <nom>)
MASses ACTivées [X/Y/Z]
[X|Y|Z] (MOIns|PLus) <liste_cas> COEfficient = <c>
Principes généraux :
Soit r = r(x), fonction de la répartition de la densité des masses sur l’élément donné et N(x), matrice des fonctions effectuant l’interpolation nodale (matrice des fonctions de la forme). La matrice des masses cohérentes sera créée en tant que base des transformations ultérieures suivant la formule générale suivante (1) :
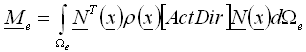 , (1)
, (1)
où :

La participation de la masse dans la direction globale est définie par la commande MASses ACTiver [X/Y/Z] c’est-à-dire que la direction est active si elle a été définie. C’est une conséquence des principes généraux du traitement des masses dans Robot où certaines composantes des forces d’inertie peuvent être négligées dans l’analyse.
La matrice des masses sera créée à partir de toutes les charges appartenant aux cas de charge spécifiés dans <case_list> agissant sur l'élément ou le noeud étudié, conformément aux règles ci-dessous :
- Chaque charge associée à un cas spécifique est convertie en masse, indépendamment des autres charges et masses.
- Seuls des cas de charge simples (pas de combinaisons !) peuvent figurer dans la liste (s'il s'agit d'un cas de dynamique, la liste des cas statiques pourra être indiquée en vue d'une conversion massique).
- La matrice des masses totale est créée en tant que la somme des matrices des masses prises de toutes les composantes des charges et des masses définies préalablement (en tant que poids propre de la structure et/ou masses spécifiées pour les éléments). Par conséquent, la partie de la matrice des masses issue des charges sera soumise à la diagonalisation et/ou la partie issue de l’inertie en rotation sera négligée si le paramètre COHérentes | CONcentrées (ROTatives) le définit.
- La valeur de la fonction de la densité dans le point donné est créée en tant que valeur de la projection courante de la force f sur le vecteur n, direction globale définie de façon obligatoire et univoque.
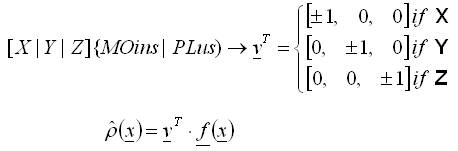 , (2)
, (2) - Seules les valeurs positives sont prises en compte dans chaque point de l’intégration de sorte que :
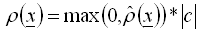 , (3) Remarque : Le but des principes ci-dessus est de permettre une sélection facile des charges résultant de l’action de la force de gravitation. Comme il n’existe rien qui ressemble à la direction par défaut de l’action de cette force, l’utilisateur doit spécifier la direction qui joue ce rôle.
, (3) Remarque : Le but des principes ci-dessus est de permettre une sélection facile des charges résultant de l’action de la force de gravitation. Comme il n’existe rien qui ressemble à la direction par défaut de l’action de cette force, l’utilisateur doit spécifier la direction qui joue ce rôle. - Toutes les directions utilisées pendant la conversion des charges en masses doivent être admissibles pour le type de structure donné. Par exemple : pour les PLAques, seule la direction Z est admise (pour les autres types de plan, seuls X et Y sont admis). Les directions incompatibles seront ignorées ou feront l'objet d'un signalement d'erreur. Pour les structures spatiales, toutes les directions globales sont admissibles.
Exemple :
Prenons une poutre au centre de laquelle une charge gravitationnelle Fy= - 120 kN est appliquée. Le cas statique représenté ci-dessous porte le numéro 3. Pour calculer les modes de vibrations propres de cette structure pour le cas n° 10 en prenant en compte cette masse (Fx=Fy= 12 232 kg), il faut utiliser la commande suivante :
ANAlyse DYN MODes=3 MASses=COHérentes
CAS #10 modal
MASses ACTiver X Y
Y MOIns 3

Description détaillée de la conversion pour tous les types de charges
Charges appliquées aux éléments de type poutre
- charge uniforme sur l’élément
[Px=<px.> /Py= <py> /Pz= <pz>] (LOCal/GLObal) (PROjeté) ([R= <r>]) ([R= <r>])
Le vecteur de la densité de la charge est converti pour les directions globales, il est déterminé par la définition :
(LOCal/GLObal) (PROjeté) ([R= <r>]), en tenant compte de (PROjeté) dans le traitement de la charge. La répartition uniforme des masses est ensuite effectuée conformément à (2) (3)
- charge permanente
La charge uniforme est convertie en masse comme la charge répartie sur l’élément.
Remarque : Soyez prudent quand vous utilisez cette opération parce que la masse provenant de la charge permanente de la structure est prise automatiquement pour les calculs dynamiques (à condition que la densité du matériau soit supérieure à zéro). - charge variable sur l’élément
(X=<x1>)[ P=<p1>] ((JUSque)(X =<x2>)[P=<p2>] ) (R=<r>) (LOCal/GLObal) (RELative) (PROjeté)
La charge est convertie pour les directions globales conformément à la syntaxe suivante :
(LOCal/GLObal) (PROjeté) ([R=<r>])
La répartition uniforme de la masse est ensuite déterminée suivant les formules (2)(3).
Remarque : La règle (3) entraîne le mode suivant de traitement du signe de la charge variable, séparément pour chaque enregistrement (composante) de la charge et non pas pour la charge totale calculée comme la somme de toutes les charges agissant sur l’élément donné (comme illustré dans la Fig.1.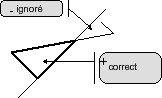 Fig. 1
Fig. 1 - force ponctuelle sur l’élément
[X=<x>] [F=<f>](R=<r>) (Local)(RELative)
La masse totale m ponctuelle sur le point x 0 est définie de la façon suivante, à partir de la représentation globale du vecteur de force f :
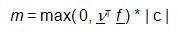 , (4)
, (4) La matrice des masses cohérentes est ensuite déterminée, comme si la répartition des masses était représentée par la fonction Delta de Dirac. On a alors :
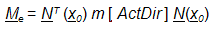 , (5)
, (5) - moment ponctuel sur l’élément
[X=<x>] [F=<fc>] (R=<r>) (LOCal)(RELative)
Comme la détermination de la direction de la masse ne concerne pas la direction de l’inertie en rotation, il faut définir une règle distincte suivant laquelle sera effectuée la conversion du moment concentré appliqué à l’élément et celle de l’inertie en rotation du certain corps attaché à cet élément.
La transformation de type vectoriel de <classe d'objets> s'effectue selon les paramètres (R= <r>) (LOCal) pour obtenir un vecteur I, repère local de l'élément. Pour contourner les incohérences inévitables dans la transformation de type vectoriel (pour les cas impliquant une transformation de type tensoriel), la charge doit être définie à l’aide de la commande LOCal et non pas R=<r>. Dans le cas contraire, un message d'avertissement s'affiche.
On suppose que le repère local de l’élément correspond à l’axe d’inertie principal du corps.
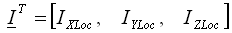 représente donc les moments d’inertie dans le repère local de l’élément. Il s’ensuit la limitation suivante de la modélisation :
représente donc les moments d’inertie dans le repère local de l’élément. Il s’ensuit la limitation suivante de la modélisation : 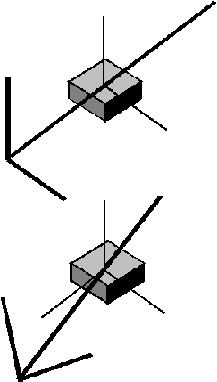
Fig. 2
Situation correcte
Situation incorrecte, la modélisation est impossible.
- moment réparti sur l’élément
[M=<m>] (LOCal)
Ici, <m> est un vecteur qui, après la transformation de type vectoriel vers le repère local de l’élément, représente la relation : densité de l’inertie en rotation (par rapport à l’axe local de l’élément) – longueur de l’élément.
Toutes les notions utilisées dans le cas du moment concentré sur l’élément sont appliquées (conf. 2).
Charges agissant sur les éléments surfaciques
- charge uniforme sur l’élément
[Px=<px.>/Py=<py>/Pz=<pz>]
Au début, le vecteur de densité de la charge est estimé, ensuite, il est transformé en densité de la masse conformément à (2)(3)
- charge permanente
La charge permanente est convertie en charge uniforme équivalente et la suite – comme ci-dessus.
Remarque : Soyez prudent quand vous utilisez cette opération parce que la masse provenant de la charge permanente de la structure est prise automatiquement pour les calculs dynamiques (à condition que la densité du matériau soit supérieure à zéro). - charge variable sur l’élément
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>))
Dans chaque point d’intégration, la densité de la charge est estimée, ensuite, elle est transformée en densité de masse conformément à (2)(3), voir la Fig. (1). Les règles d’intégration améliorées sont utilisées avec
NGAUS = 3x3 pour Q8,
= 7 pour T6,
= 2x2 pour Q4
= 3 pour T3
- charge variable à l’intérieur du contour
[P=<p1>] AU <n1>( [P=<p2>AU<n2> ([P=<p3> AU<n3>)) DIRection PROjetée <v> _CONtour <l_node>
Dans chaque point d’intégration, la densité de la charge est estimée, ensuite, elle est transformée en densité de masse conformément à (2)(3), voir la Fig. (1). Dans le cas où le contour ne contient pas toute la surface de l’élément, l’intégration automatique est effectuée – sur le maillage jusqu’à la taille 100x100 points pour atteindre la précision d’intégration exigée. Cette option pourra parfois ralentir le processus de calcul des matrices de masses.
- charge variable linéaire
LIN
<n1>[P=<p1>] Jusque <n2> (P=<p2>) ( [LOCal (GAMma=<gamma>)] )
Seule la force de déplacement peut être convertie en masse de l’élément répartie suivant une ligne.
La règle d’intégration par trois points de Gauss (3-point Gauss type integration rule) est utilisée sur chaque segment de la ligne passant par l’élément. Lors de chaque intégration, le vecteur de densité de la charge est transformé en un repère local, et la suite des opérations est conforme à (2)( 3) pour déterminer la répartition de la masse suivant la ligne.
- charge ponctuelle sur un point auxiliaire
NODe (auxiliaire)
F=<f> ( [R=<r>] )
Seule la force de déplacement peut être convertie en masse de l’élément (pour les éléments de type poutre, la conversion de la rigidité moment en rotation est permise, ici, elle est interdite). Le vecteur de force <f> est transformé vers le repère global, et la suite des opérations est conforme à (2),( 3), pour déterminer la valeur de la masse affectée au point à l’intérieur de l’élément, et ensuite, à l’aide de (5), la matrice des masses est calculée. La recherche de l’élément auquel la masse sera affectée est automatique.
Charges nodales
- force ponctuelle
NODe
F=<f> ( [R=<r>] )
Le vecteur de force <f> est transformé suivant (2), (3) pour calculer la valeur de la masse nodale.
- moment ponctuel
NODe
F=<c> ( [R=<r>] )
Comme la détermination de la direction de la masse ne concerne pas la direction de l’inertie en rotation, il faut définir une règle distincte suivant laquelle sera effectuée la conversion du moment concentré appliqué à l’élément et celle de l’inertie en rotation du certain corps attaché à cet élément.
La transformation de type vectoriel de <classe d'objets> s'effectue selon les paramètres (R= <r>) (LOCal) pour obtenir un vecteur
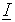 , repère local de l'élément. Pour contourner les incohérences inévitables dans la transformation de type vectoriel (pour les cas impliquant une transformation de type tensoriel), la charge doit être définie à l’aide de la commande LOCal et non pas R=<r>. Dans le cas contraire, un message d'avertissement s'affiche.
, repère local de l'élément. Pour contourner les incohérences inévitables dans la transformation de type vectoriel (pour les cas impliquant une transformation de type tensoriel), la charge doit être définie à l’aide de la commande LOCal et non pas R=<r>. Dans le cas contraire, un message d'avertissement s'affiche. On suppose que le repère local de l’élément correspond à l’axe d’inertie principal du corps.
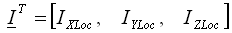 représente donc les moments d’inertie dans le repère local de l’élément. Remarque : Cette règle est différente de celles utilisées dans le cas de la masse ponctuelle attachée à l’élément de type poutre.
représente donc les moments d’inertie dans le repère local de l’élément. Remarque : Cette règle est différente de celles utilisées dans le cas de la masse ponctuelle attachée à l’élément de type poutre.