熱残留応力

一方向複合材料の熱残留応力の効果を考慮します。

**現在、熱残留応力は一方向複合材料に対してのみ計算され、織物複合材料では計算されません。

ミクロ構造効果

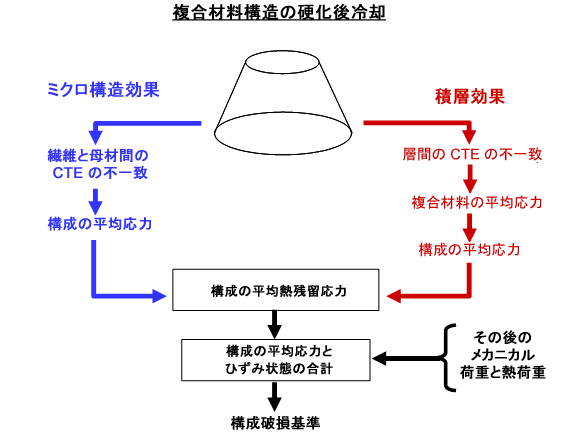
室温、T=T_amb で、孤立した荷重および拘束がない一方向複合材料層の繊維および母材構成には、非ゼロの応力状態があります。これは、硬化温度 T=T_cure から環境温度 T=T_amb への複合材料の硬化後冷却によるものです。孤立した複合材料層では、これらの熱残留応力は、母材構成と繊維構成の熱膨張係数の違いによってのみ発生します。通常、繊維強化複合材料層の硬化後冷却時には、母材構成は繊維構成よりも大きく収縮しようとします。したがって、母材構成は引張熱残留応力を示し、繊維構成は圧縮熱残留応力を示します。ただし、複合材料の平均応力状態はゼロです。これらの構成の熱残留応力は、後続の複合材料層の熱機械的荷重中に構成全体の応力状態に寄与するため、構成破損が発生する荷重に影響を与えます。

積層効果

複合材料層が、硬化後冷却中の積層に埋め込まれている場合、複合材料層で追加の熱残留応力が発生します。これは、問題の層とその近隣の層間の熱膨張係数の違いにより発生します。孤立した複合材料層とは異なり、このタイプの層間の作用は、層レベルでの複合材料の平均応力状態を非ゼロにします。つまり、層では複合材料の平均熱残留応力が発生します。これらの応力は、後続の熱機械的荷重中に繊維と母材全体の応力状態に寄与する、繊維と母材の平均熱残留応力に分解できます。したがって、応力は構成破損発生時の荷重に影響します。

構成材料レベルでのこれら 2 つのソースの熱残留応力を、次に図解しています。構成の熱残留応力が、通常の外部の機械的および構造の熱荷重の適用によって生成される構成の応力に追加されることを示しています。

Simulation Composite Analysis での熱残留応力の計算

方程式 32a-c は、一方向複合材料、母材構成材料、および繊維構成材料の線形化熱機械的構成関係(セカント定式化)をリストしています。

方程式 32a では、1 点(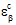)における複合材料全体のひずみ状態が、構造有限コードによって直接提供されています。一方、方程式 32b と 32c では、1 点( 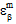および 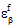)における構成全体のひずみ状態は、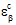の MCT 分解を使用して決定されます。温度依存の複合材料では、剛性(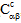、、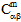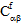)と熱膨張係数(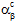、、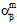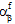)はどちらも、現在の温度 T、および繊維と母材の構成材料の現在の破損状態に依存します。温度に依存しない複合材料では、剛性(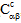、、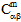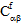)と熱膨張係数(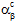、、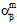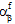)はどちらも、繊維と母材の構成材料の現在の破損状態のみに依存します。

方程式 32 の温度変化 ΔT は、通常、複合材料の現在の温度 T と複合材料の無応力時の温度 T_sf との差、つまり、ΔT = T - T_sf であると想定するでしょう。しかし、Simulation Composite Analysis で ΔT の計算に使用する実際の方程式は、複合材料の硬化後冷却中に蓄積される熱残留応力を考慮するかどうかによって異なります。適切なユーザ材料定数の整数値を使用して、任意の複合材料に対してこの機能をオンにまたはオフに切り替えることができます(『Simulation Composite Analysis ユーザガイド』の「付録 A」を参照してください)。

熱残留応力機能を「オフ」にした場合、シミュレーション中の複合材料の応答には熱残留応力に含まれません。この場合、複合材料の無応力時の温度は、既定で T_sf =0° となり、方程式 32 で使用する温度変化は単に ΔT = T - T_sf = T として計算されます。熱残留応力計算を「オフ」にした場合、いくつかの点に注意する必要があります。

複合材料データファイル(mdata ファイル)で非ゼロの無応力時の温度を明示的に定義した場合でも、無応力時の温度 T_sf は既定で 0° となります。
有限要素モデルで使用する単位系に関係なく、方程式で使用する温度変化 ΔT は、現在の温度 T によって完全に定義されます(方程式 32)。
複数の温度における特性を持つ複合材料では、現在の温度 T を使用して、方程式に示す材料特性を補間します(方程式 32)。その結果として、複合材料で熱残留応力が無視される場合、単一の温度特性(つまり、単一温度の mdata ファイル)を対象の複合材料に使用することをお勧めします。

熱残留応力は無視される場合を要約すると、現在の温度 T は方程式 32 に 2 つの異なる方法で影響を与えます。

T を使用して ΔT=T により ΔT を定義します。
T は材料特性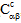、、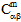、、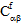、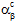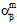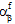の現在の値を補間するために使用されます。

熱残留応力計算機能を「オン」にすると、シミュレーション中の複合材料の応答に熱残留応力が明示的に含まれます。この場合、複合材料の無応力時の温度 T_sf は、MCT 複合材料データベースファイル(mdata ファイル)から読み取られます。ここで、T_sf は、材料の硬化温度 T_cure と同じであると認識されます。材料の無応力時の温度 T_sf が mdata ファイルで明示的に定義されていない場合は、Simulation Composite Analysis では無応力時の温度を定義する必要があることを示すエラーメッセージが生成されます。

熱残留応力計算機能を「オン」にした場合、方程式 32 で使用される温度変化は次のように計算されます。

方程式 33 で、{ } はマコーレーのカッコで、ここで {x}=0 for x<0、および {x}=x for x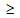0。T_amb は環境温度で、モデルで使用される単位系に応じて 72.5 °F、22.5 °C、または 295.65 °K と見なされます。

方程式 33 の右辺第 1 項により、環境温度に至る硬化後冷却の終了時(つまり、T=T_amb)の熱残留応力を正確に予測できるようになります。方程式 33 の右辺第 1 項で使用されている 1/2 の係数は、Kenik [13]の研究に基づいています。Kenik は、実際の硬化後冷却の 1/2 の温度低下を課した、室温の複合材料特性を使用した単純な線形弾性解析で生成される構成の熱残留応力が、温度依存母材特性を使用した硬化後冷却のより厳密なマイクロメカニカルシミュレーションで予測される熱残留応力とほぼ等しいことを示しました。

方程式 33 の右辺第 2 項により、硬化後冷却後に課される追加の温度低下が適切な熱応力を生成するようになります。マコーレーのカッコ { } を使用することで、方程式 33 の右辺第 2 項は、現在の温度 T が環境温度 T_amb 未満になった場合にのみ、ΔT に寄与することに留意してください。この場合(T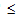T_amb)、方程式 32 で Simulation Composite Analysis によって使用される温度変化の合計 ΔT には、無応力時の温度 T_sf から環境気温 T_amb への温度変化の 50% が含まれます。さらに、環境気温 T_amb から現在の温度 T までの追加の温度低下が 100% が含まれています。ただし、現在の温度 T が環境気温 T_amb 以上である場合は、方程式 32 で Simulation Composite Analysis によって使用される温度変化化の合計 ΔT は、無応力時の温度 T_sf から現在の温度 T までの実際の温度変化の 50% のみを考慮します。この ΔT の計算方法により、材料が硬化温度 T_cure まで再加熱された場合に、熱残留応力は確実に消失することに留意してください。

MCT 複合材料特性の指定

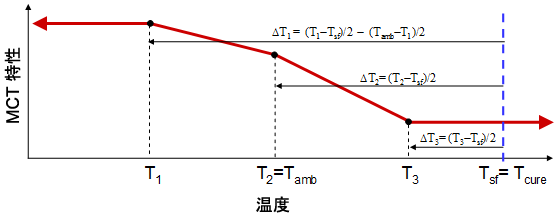
方程式 32 および 33 も、複数の温度における複合材料の特性指定プロセスで使用されます。下図は、温度依存複合材料の 3 つの異なる温度 T₁、T₂、T₃ における特性を指定する一般的な場合を説明しています。ここで、T₁<T_amb、T₂=T_amb および T_amb<T₃<T_cure。また、MCT 特性指定プロセスで、温度変化 ΔT (方程式 33 で計算)が 3 つの温度における複合材料のマイクロメカニカル解析に含まれることを示しています。特性指定プロセスで、これらの課せられた温度変化は構成破損係数の決定に影響を与えます。たとえば、マイクロメカニカルモデルを機械的に測定破損荷重レベルにロードした場合、構成材料内の破損応力状態は、機械的荷重と課せられた温度変化両方の影響を受けます。