以下に、数値流体解析方程式の計算に関連する数学的な用語について説明します
線形 - 非線形
支配方程式は次項において列記します。支配方程式には2通りの非線形性が現われます。1番目の非線形性の典型は移流項です。例えば、u流速方程式においては次の項が現われます。
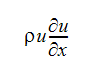
この項において、uはuの積と導関数に依存します。2番目の非線形性は、項のプロパティまたは係数が従属変数に依存するということです。例えば、エネルギー方程式における密度は、方程式が解かれる温度に依存します。また流速方程式における拡散項について、乱流に関する渦粘性は、流速への依存性が非常に高くなります。これら2つの非線形性は、数値解に対してかなり顕著な影響を与えます。そのため繰返し計算によって方程式を解く必要があります。
陽解法 - 陰解法
陰的に非線形項が処理される場合、非線形項は係数行列の一部となり解の一部となります。陽的に処理される場合は、最新の情報の代わりに前回の繰返し計算の値が使用される。通常、これらの項はソース項または荷重ベクトルの一部です。これらは、現在の収束計算後に測定されます。数値的安定のためには、できる限り多くの項を陰的に処理するのが良いと言えます。
非定常解析については、陰解法による離散化が行われます。これは、現在の時刻の値が、現在の時刻の隣接値に依存するということを意味します。一方、陽解法による離散化は、現在時刻の値が、前回の解析結果の隣接値に依存するということを意味します。陰解法は、無条件に数値的に安定しており、時間ステップサイズに関係なく解を得ることができます。ただし、各時間ステップ内で反復計算が必要とされます。陽解法は、条件付きで数値的に安定します。時間ステップサイズに関して、依存度が高く制限を受ける場合が多いのです。陽解法について1.E-10秒の時間ステップが利用される場合もあります。それにも関わらず、各時間ステップ内で繰り返し計算を行う必要はありません。
対称 - 非対称
次項において説明する支配偏微分方程式は、有限要素を使用して、解析変数の未知の節点値からなる代数方程式へと離散化されます。このような代数方程式は、次のような行列形式で表すことができます。
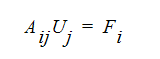
ここで、Fi は荷重ベクトル、Uj は未知ベクトル、Aij は係数行列です。対称系の方程式では、Aの上対角と下対角は対称形を成します。 すなわち、次のようになります。
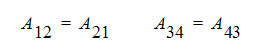
非対称系の方程式については、この限りでありません。一般的に、2次の微分項(例えば拡散項)は対称行列となり、1次の微分項(移流項)は非対称行列となります。