上述した各支配方程式は、前述の有限要素法によって離散化されます。有限要素上の節点において従属変数の値を決定するために、作成された一連の代数方程式を解く必要があります。ここでは、これらの方程式を解くために Autodesk Simulation CFD で使用されるアルゴリズムについて説明します。
分離型ソルバ
離散化方程式を解く際にまず解決しなければならない問題は、計算上不足している圧力の問題です。速度成分を計算するために運動量方程式を使用する場合、圧力を決定するために連続方程式を使用する必要があります。しかし、連続方程式において、圧力が明示的に現われることはありません。陰的な圧力連成に関する数値的問題を回避するための手段は数多く存在します。その解法の多くにおいて、有限要素メッシュの各節点上で連続方程式と運動量方程式を同時に解くことが必要とされます。小規模な問題について、この解法はかなり正確です。しかし、現実問題のほとんどについて、この解法はコンピューター資源を浪費するばかりか、問題の解を得られない場合すらあります。このような制限を緩和するため、圧力に関する陽的な方程式を導く必要があります。
Autodesk Simulation CFD で解く圧力方程式は、連続方程式から導かれます。ここで、連続方程式に重み積分が用いられ、積分の次数を減らすために部分積分が使用されます。
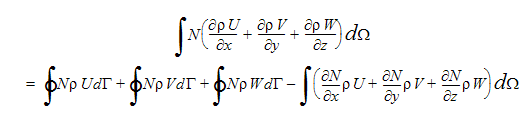
この方程式の右辺(RHS)の最初から3つの積分は、要素の境界上の質量流束です。これらの積分は、内部の要素面において消去され、質量が流れない全境界(対称、壁)についてゼロとなります。したがって、これらの項は、圧力方程式の自然境界条件を表します。
この方程式において圧力が現われるように、流速と圧力間の関係が導かれなければなりません。この関係は、運動量方程式により推定することができます。運動量方程式の半離散化形式を用いて、流速-圧力の関係を以下のように表すことができます。
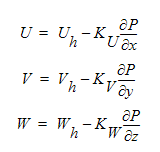
以上の方程式において、U h 項・V h 項・W h 項は、運動量方程式内の全ての非対角項を含みます。これら3つの方程式を前述の連続方程式に代入すると、次の圧力方程式が導かれます。
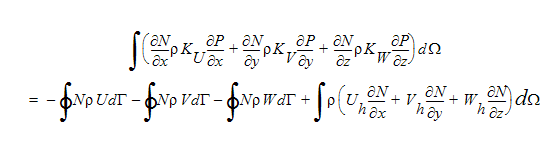
この方程式は、ポアソン方程式の離散化形式です。 そのため、対称な係数行列が生じることに注意してください。
圧縮性流れの場合、密度-圧力の連成も考慮する必要があります。この連成は、以下の方程式を用いて記述されます。
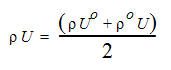
ここで、oは以前の値を意味します。この表現は、連続方程式を部分積分する場合に使用されます。その後、流速と置換すると、以下が与えられます。
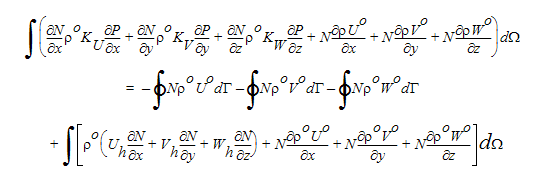
この方程式の左辺の特別な移流項は、理想気体の法則を使用して、圧力の点から再記述されます。圧縮性圧力方程式は、これらの移流項によって、その他の輸送方程式と同様、非対称な係数行列を導きます。
陽的な圧力方程式により、それぞれの支配方程式を別々に解くことができます。すなわち、X方向運動量方程式を全ての節点においてUに対して解き、Y方向運動量方程式を全ての節点においてVに対して解き、Z方向運動量方程式を全ての節点においてWに対して解き、圧力方程式を全ての節点においてPに対して解くことができます。 このことにより、一度に1つの自由度のみが解かれるため、必要なメモリー量を大きく減少させることが可能です。各従属変数が別々に解かれるため、このアプローチは 分離型ソルバ と呼ばれます。また、これらの方程式はそれぞれ反復法を使用して解くことができるため、係数行列内のゼロ以外の項のみを保存するだけで済みます。