流体流れの定義

非圧縮性－圧縮性

圧縮性という用語は、密度と圧力の関係について述べたものです。流れが圧縮性の場合、流体の圧力の変化が密度に影響を与え、逆に、密度の変化も圧力に影響を与えます。圧縮性流れは、非常に高速なガスの流れです。

圧縮性流れと非圧縮性流れ間の大きな違いの1つは、物理的な圧力の性質にあり、そのため、圧力方程式の数学的特徴が大きく異なります。非圧縮性流れの場合、下流の影響があらゆる領域にすぐに伝播し、圧力方程式は数学的に楕円型となるため、境界条件を下流にも設定する必要があります。圧縮性流れ、特に超音速流の場合、上流のいかなる領域にも下流の圧力は影響を与えず、圧力方程式は双曲型となり、境界条件は上流のみに設定する必要があります。

下流の境界には圧力の拘束を与えてはいけません。

マッハ数

圧縮性の判断基準の1つにマッハ数があります。以下のように定義される音速により流体の流速を除算し、マッハ数が定義されます。

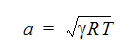
ここで、a は音速、gamma は比熱比、R は一般ガス定数、T は静温度です。マッハ数が0.3未満の場合、流れは非圧縮性と考えられます。この値を超えると、圧縮性の効果は、より影響力を持つようになり、正確な解を得るために考慮されなければなりません。

断熱圧縮

伝熱の影響がなく、音速（マッハ＝1.0）未満で流れが移動している場合、その流れは断熱的であると考ることができます。このタイプの流れの場合、全エネルギーが保存されます。すなわち、運動エネルギーと熱エネルギーの和が定数です。方程式にすると、次のように表すことができます。

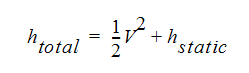
ここで、Vは流速、 hはエンタルピー（エネルギーの単位）です。理想気体を想定して、この方程式は温度を使用して表すことができます。

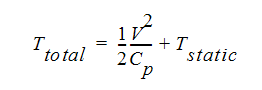
ここで Cp は定圧比熱で、次の式を用いて与えられます。

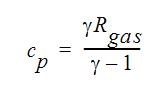
ここで、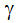は定積比熱に対する定圧比熱の比、Rgas は使用する気体のガス定数です。全温度は よどみ点温度 とも呼ばれます。この式のの右辺第1項は、動温度とも呼ばれます。

遷音速／超音速／極超音速流

これらの3つの用語は、圧縮性流れの分類に使用されます。遷音速流は、音速であるか音速に近い速度です。マッハ数が1<Ma<5の範囲の場合、超音速です。マッハ数が5を超える流れは、極超音速と呼ばれます。遷音速流と超音速流は、理想気体の仮定を使用してモデル化することができます。

極超音速流は、理想気体の仮定を使用してモデル化することはできず、実在気体の影響を考慮する必要があります。

絶対圧、全圧、静圧、動圧

絶対という用語は圧力とあわせて使用されます。通常、圧力方程式に対する解は、相対圧力です。この相対圧力は、重力ヘッドや回転ヘッド、参照圧力を含みません。相対圧力は、運動量方程式において、直接流速の影響を受ける圧力です。絶対圧力は、圧力方程式により計算された圧力に、重力ヘッド・回転ヘッド・参照圧力を追加します。相対圧力をPrelとすると、絶対圧力は次の式によって与えられます。

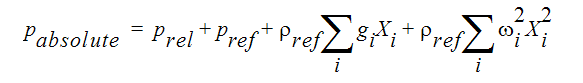
ここで、添え字 ref は参照値を意味し、添え字 i は 3 つの座標方向を意味し、g は重力加速度、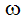は回転速度です。参照圧力と参照温度を使用して、解析の最初に参照密度が計算されます。密度が一定の流れについて、参照密度は一定の値です。重力ヘッドまたは回転ヘッドを持たない流れについては、相対圧力はゲージ圧です。

動的および静的という用語は、通常、圧縮性流体について使用されます。動的な値は、運動エネルギーなどの項です。

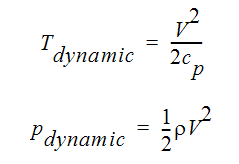
動温度を計算するために使用される比熱は、プロパティウィンドウ上で入力された温度の値ではなく、次の式によって与えられる機械的な値であることに注意が必要です。

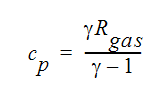
ここで、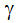は定積比熱に対する定圧比熱の比、R_gas は使用する気体のガス定数です。

静温度は、エネルギー方程式を解いて決定されます。断熱的なプロパティについては、静温度を決定するために使用されるエネルギー方程式が、一定の全温度方程式となります。したがって、静温度は、全温度またはよどみ点温度から動温度をさしひいた温度です。

静圧力は、前述の絶対圧力です。全温度は、静温度と動温度の合計です。全圧力は、静圧力と動圧力の合計です。

層流-乱流

層流は、滑らかで一様な流体の動きを特徴とします。乱流は、変動し波立った動きを特徴とします。流れが層流であるか乱流であるかの判断基準は、流体の速度です。一般的に層流の速度は、乱流の速度よりはるかに遅いものとなります。流れを層流または乱流に分類するために使用される無次元数はレイノルズ数で、以下のように定義されます。

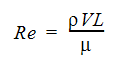
ここで、は密度、V は流速、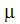は粘度です。2500より大きなレイノルズ数の場合、流れは乱流の現象を示します。通常、工学的な流れは乱流である場合が多いといえます。

層流と乱流の中間領域は、遷移流の領域です。この遷移流領域において、流れは非線形の性質の段階をいくつか経て、完全な乱流に発達します。それらの段階は非常に不安定で、流れは急速に1つの性質（乱流スポットなど）から別の性質（渦崩壊）に変化したり、元に戻ったりします。このように不安定な性質の流れのため、数値的な予測が非常に困難です。

非粘性－粘性流

粘性やせん断応力の影響が無視される流れを非粘性といいます。粘性流は、粘性またはせん断応力の影響を有します。全ての流れが粘性を持ちます。しかしながら、せん断応力の影響を無視して有意義な結果を得ることが限られた事例がいくつか存在します。

非粘性の流れは、オイラー方程式を用いて解くことができる理想流体として分類されます。これらの方程式は、Navier-Stokes方程式のサブセットです。圧縮性流れ解析コードの中には、Navier-Stokes方程式の代わりにオイラー方程式を解くものがあります。方程式の数学的特性が変化しないため、オイラー方程式を解くのは、数値的により容易です。粘性の効果を考慮する場合、楕円型方程式の影響に支配される領域と双曲型方程式の影響に支配される領域の双方が計算領域に含まれます。これは、取り組むのがはるかに困難な問題です。

非粘性の流れが非回転でもある場合、速度ポテンシャル関数を定義して流れを表すことができます。そのような流れをポテンシャル流れと呼びます。単一方程式を解いて全ての流れパラメータを決定することができるため、このタイプの流れについても、オイラー方程式を解くよりは数値的に容易です。非粘性で非回転であるという前提は、非常に制限された条件です。しかし、ポテンシャル流れの解により、非常に制限された類の流体流れ問題について、フローパターンに関する情報を得ることができます。

境界層流れ

サーフェス上を流体が流れる場合、境界層が形成されます。サーフェスに沿って移動するとともに、この境界層は発達します。流体せん断応力は、主として境界層に存在します。このせん断層の発達を主に取り扱う流体流れ問題として、境界層流れは分類されます。境界層流れは、サーフェスに隣接している、あるいは噴流の場合が多くなります。

ほとんどの境界層流れにおいて、境界層における圧力は実質的にほぼ一定です。境界層外部において、圧力勾配は大きく変化し、境界層流れに影響を与えています。このタイプの流れは、境界層が成長する方向に沿って情報が基本的に一方方向に伝達されるため、数学的に放物線として特徴付けられます。

ニュートン／非ニュートン流体

ニュートン流体とは、流体せん断応力とせん断速度間に線形関係を示す流体です。

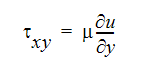
ここで、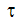は流体せん断応力、速度勾配はせん断速度テンソルの 1 方向成分、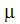は粘性係数です。ニュートン流体の粘性は、一定であるか温度の関数です。非ニュートン流体については、粘性がせん断速度の関数でもあるため、せん断応力はせん断速度の非線形関数となります。

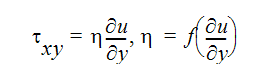
非ニュートンべき乗流体に関して、せん断応力は次のように表されます。

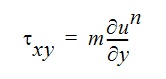
ここで mコンシステンシー指数、nはべき乗指数である。粘性の点から、この方程式を次のように表すことができます。

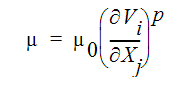
ここで、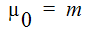、p = n - 1 です。

ハーシェル - バックレー非ニュートン流体は、次のように記述することができます。

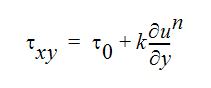
粘性の点から、次のように表すことができます。

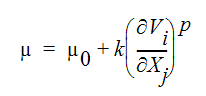
他の非ニュートン流体は、カリューモデル流体として表されます。

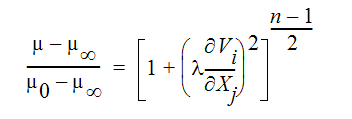
ほとんどの工学的な流れはニュートン流体（空気・水・オイル・蒸気など）です。非ニュートンと考えられる流体には、プラスチック、血液、懸濁液、ゴム、製紙用パルプなどがあります。

熱伝導／対流／複合／熱放射伝熱

熱の伝達には3つの形態があります。熱伝導において、熱は分子運動によって伝達されます。その伝熱量は、熱伝導率に依存すします。対流伝熱は、流体運動によって輸送される熱として定義されます。放射伝熱は、光学的な条件に依存する電磁気の現象です。複合伝熱は、以上3つの形態のうち2つまたは全てが組み合わさった現象です。

サーフェス間の熱放射

ほとんどの工学問題について、固体のサーフェスから別のサーフェスへの放射エネルギー交換が発生します。固体に囲まれた内部の気体は、一般的に熱放射に関与しません。ただし、加熱炉などにおいてガスが燃えたり熱せられる場合は別です。サーフェス間の熱放射交換は、サーフェスの温度に影響を与えます。そのため、対流または熱伝導が起こり、ガスの温度が影響を受けます。支配方程式に熱放射交換を含めるため、付加的な熱流束項 q_ri が壁面要素に追加されます。この項は、次の式によって与えられます。

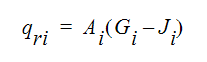
ここで、q_ri はサーフェス間の熱放射から要素 i における流体への正味熱流束です。G_i は要素面 i 上の入射光、J_i は要素面 i の放射照度です。放射照度は次の式で表すことができます。

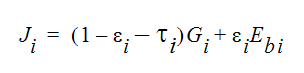
ここで、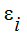は輻射率、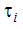は要素面 i の透過率、E_bi

は要素面 i の黒体放射です。

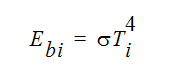
ここで、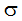はステファン - ボルツマン定数です。入射光は、次の式を用いて与えられます。

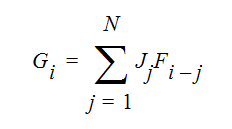
ここで、F_i=j·は要素面·i·と要素面·j·間の形態係数です。したがって、放射熱流束を計算するには、すべての要素面間の形態係数を計算する必要があります。

Autodesk Simulation CFD には、形態係数を計算するための方法が 2 つあります。1つめは以前のバージョンにもあった方法で、レイトレーシング法と離散座標法を組合せたものです。このモデルでは、要素面の外表面のすべてにそれを囲む半球面を作成し、この半球を無数の離散的な放射状の線に分解します。Autodesk Simulation CFD は、この放射線が他の要素面に当たるかどうかを探索し、当たれば双方の要素面間での放射熱交換を行います。

2 つ目の新しい方法(放射モデル 4)では、Autodesk Simulation CFD は表面の要素面を囲むような球面に投影します。これによって、球面上に要素面のマップができます。この投影マップから、Autodesk Simulation CFD は形態係数を正確に算出することができます。この方法で算出する形態係数の精度は、投影マップの解像度に依存します。次に、Autodesk Simulation CFD は次の式に示す形態係数の相反性を確保します。

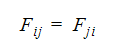
この形態係数の相反性の確保することにより、放射熱エネルギーバランスもまた厳密に守られます。この2つめの新しい手法は、旧バージョンの手法よりも高精度であるが、形態係数の計算に(一時的にではあるが)より多くのメモリとCPUパワーを必要とします。しかし、形態係数の計算は一度行って保存すれば、リスタートの際に形態係数の再計算をすることはありません。

放射モデル 4 のその他の特徴としては、形態係数の計算により、Autodesk Simulation CFD で太陽熱流束の計算が可能になります。太陽放射の計算のため、モデル全体を覆う空を模擬するためドーム形状の計算を行います。ドーム(空)と部品間の形態係数が、部品への太陽放射伝熱を決定します。太陽熱流束は、時刻、緯度、経度に従って Autodesk Simulation CFD により自動的に計算されます。

自然/複合/強制対流

これらの用語は対流伝熱の種類を示すために使用されます。自然対流においては、流体のプロパティ、特に密度に影響を与える温度差によって流動が引き起こされる、あるいは支配されます。また、運動量方程式の重力項あるいは浮力項が流れを支配するため、このような流れは、 浮力流れ とも呼ばれます。これに対し、強制対流においては、流動により温度が支配され、浮力または重力の影響はほとんどありません。複合対流は、これら2つが組み合わさった流れで、流動と浮力の両方が影響します。自然対流には、開口部や明確に定義された流入口が存在しない場合が多くなります。強制対流には、常に流入口領域と流出口領域が存在し、複合対流の場合も同様です。自由対流は、囲まれていない自然対流あるいは開いた自然対流の問題です。

Autodesk Simulation CFD では、密度を一定とするブシネスク近似を使用していません。その代わり、圧力の単純化のため、以下の低マッハ数近似を使用しています。

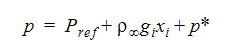
ここで、P_ref は参照圧力(通常は大気圧)、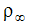は参照密度(参照圧力、参照温度における密度)、g_i は重力加速度ベクトル、x_i は原点からの位置ベクトルです。この式を運動量方程式に代入すると、新しい従属変数は p* になります。静的ヘッド(右辺第2項)を引けば、数値計算の安定度は大きく向上します。

対流問題は、層流の場合も乱流の場合もあります。強制対流や複合対流においては、レイノルズ数が流れの様相を判断するための指標となります。自然対流についてはグラスホス数が基準となります。グラスホフ数は、以下のように定義されます。

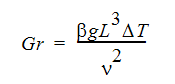
ここで、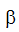は体積膨張率、g は重力加速度、L は特性長さ、T は温度、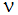は動粘性係数です。グラスホフ数とプラントル数の組合せであるレイリー数が参照される場合もあります。

プラントル数は、以下のように定義されます。

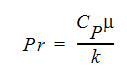
レイリー数は次のように定義されます。

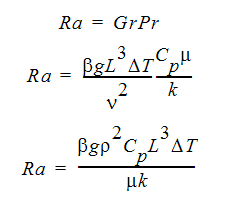
ここで、C_p は定圧比熱、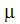は絶対粘度、は密度、k は熱伝導率です。

熱伝達率

Autodesk Simulation CFD は、熱伝導率(対流)を 2 つの方法のいずれかで計算します。1番目の方法は、熱残差を計算する方法です。熱残差は、エネルギー方程式を作成し、最後の温度（またはエンタルピー値）の解をその方程式に代入することにより計算されます。残差とは、解の温度を維持するために必要な熱量です。

次の関係より熱伝達率を決定するために伝熱残差が使用されます。

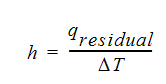
ここで、温度差は、壁値と壁近傍の値との差です。

2番目の方法は、レイノルズ数に基づいた実験から得られた関係式を使用する方法です。実験結果から、以下のように定義されるヌセルト数の計算が必要となります。

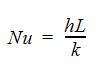
ここで、hは熱伝達率、Lは代表長さ、kは熱伝導率である。ヌセルト数とは、熱伝導伝熱量と対流伝熱量の比率です。Autodesk Simulation CFD がヌルセト数の計算に使用する相関は、次のとおりです。

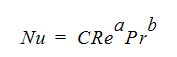
ここで、Prはプラントル数、aとbとCは定数です。ヌッセルト数とレイノルズ数は両方とも代表長さに依存することに注意します。代表長さは必ずしも同一ではなく、異なる場合が多いと言えます。通常レイノルズ数の代表長さは、開口部の長さ（シリンダーの直径またはステップの高さ）です。一般的にヌセルト数の代表長さは、熱伝達率が計算されるサーフェスに沿った長さです。

バルクおよび平均値

独立変数の平均値を表す方法として２種類の手法があります。第１の方法は、次式によって計算される質量重み平均値で計算されるバルク値です。

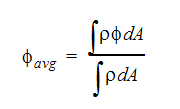
この式では、バルクを解析領域内のある位置で計算します。積分はその位置にある要素面全体で行われます。

平均値を計算するもう１つの方法は、次式で計算される算術平均値を使用する方法です。

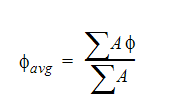
これらの２つの方程式より、質量重み付きの平均値と算術平均が必ずしも一致しないことがわかります。例えば、流速の算術平均値は、次式で計算されます。

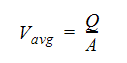
しかしながら、バルク流速はこの等式を満足しません。

分布抵抗

数多くの障害物が存在するジオメトリの場合、分布抵抗を使用して問題の全体的な規模（有限要素数）を縮小することができます。圧力勾配と流速勾配を解くために必要な詳細な設定を行って流れ障害物のそれぞれをモデル化するのではなく、流れ障害物をより大きな規模でモデル化し、運動量方程式における減衰項として表すものです。流れ障害物は、追加圧力損失として、効果的にモデル化することができます。例えば、多管円筒形熱交換器における管の部分について、それぞれの管をモデル化するのではなく、分布抵抗を使用してモデル化することができます。このモデリングテクニックにより、ベント、ルーバー板、充填層、格子、チューブバンク、カードケージ、フィルター、その他の多孔質媒体のモデル化を行えます。

分布抵抗項の形式には3通りあります。1番目の形式は損失係数で、付加される圧力勾配は次のように記述されます。

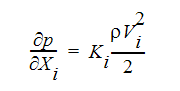
ここで、iはグローバル座標方向を示します。損失係数Kは、流量に対する圧力損失の大きさから決定することができます。また、この係数は、Handbook of Hydraulic Resistance, 3rd edition（I.E. Idelchik著、1994年CRC Press発行［ISBN 0-8493-9908-4］）などの流体抵抗ハンドブックより入手可能です。Autodesk Simulation CFD で使用されている損失係数 K には、長さ -1 の単位があることに注意してください。ほとんどのハンドブックが使用しているのは、単位のない損失係数Kです。

2番目の分布抵抗の入力形式は摩擦係数です。この形式において、追加される圧力勾配は次のように記述されます。

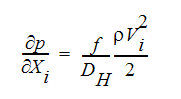
ここで、f は管摩擦係数、D_H は水力直径です。摩擦係数は、ムーディの式を用いて計算することができます。

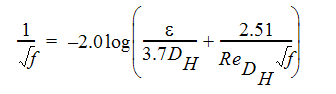
ここで、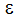は長さ単位での表面粗さ、DH_H は長さ単位での水力直径です。

摩擦係数は、次の関係式を用いて計算することもできます。

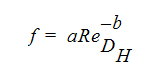
ここでaとbは定数です。

最後の分布抵抗項の形式は、ダルシー則に従います。

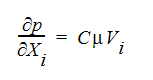
ここで、C は透水係数、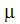は流体の粘性係数です。

どの形式を使用するかは、利用可能な圧力損失に関する情報に大きく依存します。前述の通り、流量に対する圧力損失データが入手可能な場合、Kファクターの利用が最適でしょう。一方、充填層の場合、透水係数を使用できるものがあり、この場合は最後の形式が最適です。また、一連の管からなる大規模なジオメトリに対しては、摩擦係数が最適な形式であると考えられます。