離散化処理は、全節点における代数方程式を作成します。これらの方程式は行列Aijを形成します。Aijは、有限要素の節点と同一数の行と、節点の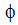
値に関するゼロ以外の係数を保持するに十分な列となります。
行列方程式の伝統的な計算方法はガウス消去法です。これは、解を得るためには比較的非効率な方法です。 なぜなら、この消去処理は、分解処理を行う際、最低1つのバンド行列を必要とするためです。Autodesk Simulation CFD によって保存される Aij は、そのバンド行列よりはるかに小さものです。また、消去処理は、極端にコンピュータ資源を浪費します。方程式が繰り返し解かれるため、この非効率的な消去法の計算は非常に遅く大変な作業となります。
消去法を使用する代わりに、反復行列ソルバーを使用する方法があります。 この方法においては、計算数を低減し、代入処理を完全に除外するために推定値が与えられます。したがって、ゼロ以外の行列のみが必要とされ、コンピューターの必要資源が大幅に縮小されます（3次元問題において2～3次数）。具体的に言うと、この近似では、一つ前の計算値 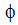が現在の推定値として利用されます。ソルバーによる繰り返し計算は、最終的に丸め誤差のない、ガウス消去法と同一の解を与えます。しかし、方程式の非線形性のため、この段階に達する前に繰返し計算を停止しなければならない可能性があります。
最も単純な反復行列ソルバーは、 値が次の式より決定されるGauss-Seidel法です。
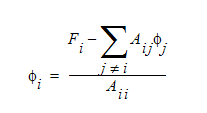
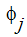の値は、最も新しい利用可能な値です。実質的に、これは、全ての非対角項を方程式の右辺に移動します。適当な解を得るために繰り返される計算数が非常に多いため、Gauss-Seidel法はあまり使用されません。
特に輸送問題について、Gauss- Seidel法よりかなり望ましい解を与えるその他の反復行列ソルバーは、3重対角行列アルゴリズム（TDMA）です。この方法においては、3重対角行列方程式が作成されます。ここでは、係数行列の対角線に隣接する2列が保持され、その他の項は、方程式の右辺に移動され、íの一つ前の値が利用されます。TDMAに関する行列方程式は次のように表されます。
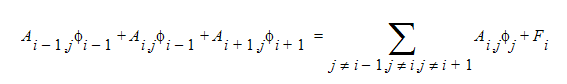
TDMAアルゴリズムは、節点の1次元平面を同時に効果的に解きます。輸送方程式において、情報は、入流口面から継続する平面にそれぞれ伝達されます。したがって、輸送方程式の計算にTDMAアルゴリズムを利用すると、この物理的な情報の流れが模擬されます。
いくつかの共役勾配法の改良型である反復行列ソルバーが存在します。その中には、対称行列のみに適用できるものがあり、その以外は、非対称行列に適用されます。このような改良型ソルバーは全て、同様の手法を用いて行列方程式を解きます。すなわち、行列式の解を導き、収束を高速化するため、検索テクニックを使用します。また、高い精度の解を与えるため、半直接行列ソルバーと呼ばれることもよくあります。Autodesk Simulation CFD において、収束の判断基準に到達するか、ユーザによって設定された反復計算数を超過しない限り、共役勾配ソルバは、消去処理を通して反復計算を実行します。