非定常解析の場合、非定常項は、陰解法または後退差分近似法によって離散化されます。行列代数を用いて、典型的な定常状態の輸送方程式（運動量・エネルギー・乱流変数・スカラー）が与えられます。
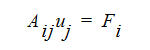
ここで、Aij は、支配方程式から離散化された移流項と拡散項、uj は、従属変数(u、v、w、T、K など)の解ベクトルまたは値、Fi はソース項です。
支配方程式における非定常項は、次の形式で表されます。
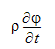
ここで、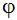
は従属変数（u・v・wなど）です。この項は、以下の後退差分近似を用いて離散化されます。
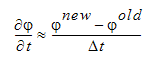
これを上記の行列方程式に追加することができます。
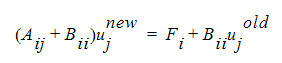
ここで、Bii は、次のような項により構成される対角行列です。
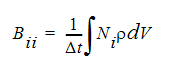
この離散化された非定常方程式は、新しい変数（最後の変数値）を全て決定するため、それぞれの時間ステップにおいて 繰り返し計算によって解かれなければなりません。