Autodesk Simulation CFD では、有限要素法を使用して、支配偏微分方程式(PDE)を一連の代数方程式に変換しますこの方法において、従属変数は小さい面積あるいは体積(要素)上にて、多項式の 形状関数によって表現されます。これらの表現が支配偏微分方程式に置き換えられ、形状関数と同じものとして選択された 重み関数を使用し、要素の方程式の重み積分が実行されます。結果として、各要素上の離散点または節点における従属変数に関する一連の代数方程式が与えられます。
流線上流法対流項計算スキーム
連続方程式を除き、支配方程式は、計算領域全体の出力量(例えばU、V、Tなど)の輸送を記述します。支配方程式は次の形式で表されます。
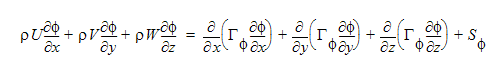
一般スカラー輸送方程式も、ソース項を持たないが、この形式であることに注意してください。
上述の有限要素法は、拡散項およびソース項において直接使用されます。しかし、数値計算の安定性のため、 対流項は 対流項は 重み積分法とともに流線上流法が使用されます。Autodesk Simulation CFD で使用する 4 つの上流法を下記に示します。
ADV 1: 単調流線上流法
- 数値的に安定
- 1 < 次数 < 2
- 流れ方向に沿った要素分割に推奨
- 要素分割が流れ方向に沿ってない場合は発散しやすい
- 流れの障害となるジオメトリが多く存在する場合に有効
- 押出しメッシュに有効
ADV 2: ペトロフ-ガラーキン法
- 数値的に安定 (ただしADV 1よりも安定度低い)
- 2 < 次数 < 3
- ランダムなメッシュでも発散しにくい
- 圧力によって生じる流れに有効
- 圧縮性流れに有効
- スカラー/エネルギー輸送方程式のデフォルト
ADV 3: 熱流束ベースのスキーム
- 多くの流れに対し、数値的には不安定
- 次数 > 3
- 対流項に複数要素の上流法を使用
- 非圧縮性流れのみに対して有効
- 移動固体の解析には使用不可
- 外部流れや抗力計算に非常に有効
ADV 4: Min-Mod スキーム
- ペトロフ-ガラーキン法に類似の方法
- 2 < 次数 < 3
- 数値的に安定 (ただしADV 1よりも安定度低い)
- 長く狭いダクト内の流れに非常に適している
上流法による対流項取扱いの例として、ADV 1を紹介します。この上流法では、対流項は流線に沿う座標系に変換されます。
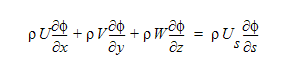
ここで s は流線に沿う座標方向、 Us はs方向の流速です。純粋な対流問題では、この項は一定値となります。これを考慮すると、重み積分付き対流項は次のように表されます。
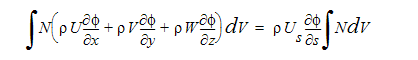
この他の対流項計算スキームでは、要素内の流線を表せるよう、形状関数を修正します。