サマリーァイルには、選択した変数に関する節点の最小値、最大値、平均値が表形式で保存されます。すべての流入部および流出部における質量流量、バルク圧力、温度、およびレイノルズ数に対する全体的なサマリー計算値が含まれます。またモデル全体に対する壁の伝熱計算、全体エネルギーバランス、流体力などがレポートされます。
解析実行時の統計と使用されるRAM量がリストされます。
サマリーファイルには、".sum"という拡張子があり、任意のテキストエディタで表示できます。
解析計算ユニットおよびすべての変数の単位がファイルに含まれます。
開口部
すべての流速境界条件には「inlet」、すべての圧力境界条件には「outlet」というラベルが付きます。これは記録のためであり、モデル内外への流れの方向には基づいていません。
各開口部に対して以下の値が出力されます。
- 質量流量（流入または流出）
- 体積流量（流入または流出）
- レイノルズ数
- バルク圧力（流入口または流出口）
- バルク温度（流入口または流出口）
- マッハ数（流入口または流出口）
- 全質量流量（流入または流出）
- 全体積流量（流入または流出）
流入口と流出口に指定圧力が生じる圧力による流れの場合、サマリーファイルには流入口はなく、2個の流出口があると記録されます。実際の流入口は正の質量流量を持ち、実際の流出口は負の質量流量を持ちます。また、「全質量流入量」および「全質量流出量」はゼロになることに注意してください。なぜなら、流速条件が指定されておらず（ラベルの付けられた流入口が存在しない）、ラベルの付けられた流出口からの全質量流量が相殺される（1つが正で1つが負）からである。
レイノルズ数についての注意:
基本的な形式のレイノルズ数は、以下のように計算されます。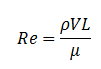
- V = 断面を通過する平均流速
- L = 特性長さ
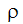= 流体密度 
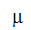= 流体密度
断面上の平均流速は、以下のように計算されます。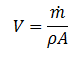
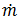= 質量流量 - A = 断面面積
特性長さ L は、断面面積の平方根として計算されます。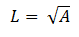
結果として生じるレイノルズ数の方程式は、以下のようになります。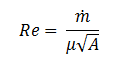
温度の統計値
伝熱を伴う解析の場合、温度分布に関する統計値がサマリーファイルに含まれます。これらの統計値は、特定の範囲内の温度がどの程度（ボリュームパーセントとして）モデルに分布しているかを示します。
壁面における流体力のサマリー
合計された力の成分がサマリーファイルに、せん断力と圧力として表示されます。これらの値は、モデルの全壁面の値を合計したものです。個々のサーフェスにおける力を計算するには、結果タスクダイアログの壁面の計算を使用します。
シェルに作用する力
解析にシェルが存在する場合（固体サーフェスあるいは障害物）、力、温度、伝熱量の情報がそれぞれのサーフェスについて、サマリーファイル中にリスト表示されます。
エネルギーバランス
| ライン | 流体エネルギー バランス情報: |
| 1 | MdotIn x Cp x (TOut - TIn) |
| 2 | (数値) 流出エネルギー - 流入エネルギー |
| 3 | 壁から流体までの熱伝達 |
| 4 | 流体内の熱源による熱伝達 |
| 5 | 流体壁面への総輻射熱伝達 |
| 固体エネルギー バランス情報: | |
| 6 | 外部から固体までの熱伝達 |
| 7 | 流体内の熱源による熱伝達 |
| 8 | 流体から固体までの熱伝達 |
ライン 1: 流出口から流入口までの流体のエネルギーの物理的な差です。
ライン 2: 流出口から流入口までの流体のエネルギーの差です。これは流体領域の増加エネルギー量の合計です。流体境界条件を維持するために必要なエネルギー量を示している。これは、次式に等しくなります: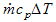 
(ライン 1)。
ライン 3: これは、流体が壁面の節点または固体中の界面上の設定から受け入れたエネルギー量を表しています。流体の外部表面が断熱（その他のボリュームやサーフェスに接していない）の場合、流体の得たエネルギーの総量は、固体材料から得たことになります。流体の外部表面上に熱境界条件が存在する場合、ライン 3 には固体材料からのエネルギーと同様、外部表面境界条件からのエネルギーも含まれます。
ライン 4: これは流体要素/ボリュームの熱源からのエネルギーの合計です。
ライン 5: ライン 2 ～ 4 とライン 6 ～ 8 から計算されるエネルギーは放射(輻射)エネルギーを含みません。このラインは、すべての壁面からの放射熱流束を合計したものです。
ライン 6: これは、固体材料の外部表面節点に流入するエネルギー量の合計に相当します。これは、固体材料の外部面にあるエネルギー量の合計です。これらの面は、他の媒体に接していない面です。場合によっては、固体材料およびその外部表面に熱発生の条件が設定され、この行が外部節点上の残差を合計する有限の数字となることがあります。この場合には、この数字は、材料から環境に放出されたエネルギー量であると解釈されなければなりません。外部境界に熱流束が設定されるあるいは一定温度が設定されたケースでは、このラインは、これらの境界条件を維持するために必要とされるエネルギーの合計量を示します。
ライン 7: これは、固体内の熱源によって発生した熱量の合計を表します。
ライン 8: これは、流体から固体へのエネルギー伝達量を表します。流体の外部が断熱壁の場合、このラインは、ライン 3 と同じ値となります。
流体のエネルギーバランスについて、次の式が満足されなければなりません。
流出エネルギー - 流入エネルギー = 壁から流体までの熱伝達 + 流体内の熱源による熱伝達 + 流体壁面への輻射熱伝達
あるいは
ライン 2 = ライン 3 + ライン 4 + ライン 5
固体のエネルギーバランスについては、次の式が満足されなければなりません。
固体内の熱源による熱伝達 = 外部から固体までの熱伝達 + 流体から固体までの熱伝達 + (一部の輻射)
あるいは
ライン 7 = ライン 6 + ライン 8 + (一部の輻射)
熱放射(輻射)の計算については、固体からの放射エネルギーが放出されて留まらないため、ライン 8 はライン 6 よりも大きな値となります。
正確に一致しない場合はどうすべきだろうか？解析モデルの全節点についてエネルギー方程式の増加量を合計しているからです。エネルギー方程式が完全に収束していない場合、これらは完全にはバランスしません。収束した状態についても、エネルギーバランスには、まるめ誤差やメッシュの不完全性により、いくらかの誤差が含まれる可能性があります。
さらに、Autodesk Simulation CFD のゴールは、温度の項に関して最も正確な解を得ることであるということに注意が必要です。したがって、Autodesk Simulation CFD のソルバは、最高な解を決定するためにエネルギー バランスを使用していません。ただし、ソルバは、直接エネルギー方程式と温度の解を求め、最適な温度の解を得ることができるよう最適化を行っています。エネルギー方程式が熱流束に基づいて作成された場合、収束解に達していない場合でも常にエネルギー バランスが充足される可能性があります。しかしながら、この熱流束のバランスは、エネルギーバランスを維持するために、温度のしみや拡散が必要となるかもしれません。この熱流束のバランスは、温度勾配を緩やかにするかもしれません。Autodesk Simulation CFD では、熱流束またはエネルギー バランスを充足するために温度勾配を人為的に変更することはなく、メッシュと離散化がサポートする急勾配を維持します。一般的に温度は設計を制約するため、より高い局所的な温度の解が必要とされます。
Autodesk Simulation CFD でエネルギー バランスを充足することはできますか。もちろん、できます。ただし、より細かいメッシュ、100回あるいはそれ以上の収束計算が必要かもしれません。メッシュと収束計算の追加は、自由度の10分の1あるいは100分の1も変更しないかもしれませんが、エネルギーバランスを20%あるいはそれ以上変更する可能性があります。
下図に示す伝熱問題の例題では、質量流量が1kg/sであり、入口温度に対する出口温度の上昇が1℃となり、エネルギー流入量が100W（流体の比熱が100）となることが期待されています。
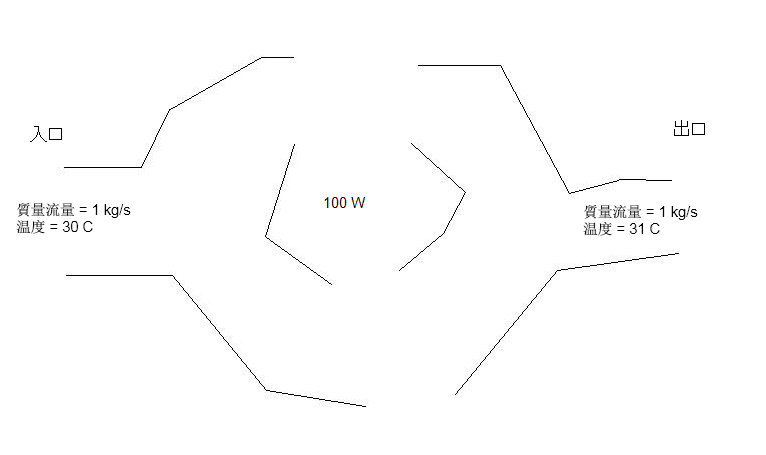
Autodesk Simulation CFD で計算された出口温度が 31.1 ℃ の場合、エネルギー バランスの誤差は 10% です。しかしながら温度の誤差は、以下の値ととなります。
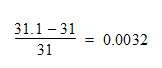
つまり、温度の誤差は1%以下です。温度の行列が絶対温度として作成された場合、温度の解析結果の実際の誤差は以下の値となります。
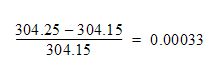
従って、温度の誤差は0.03%です。