Informacje o definicjach krzywej przejściowej

W inżynierii lądowej i wodnej stosowane są różne typy krzywych przejściowych do stopniowego wprowadzania krzywizn i przechyłek między stycznymi i łukami kołowymi, a także między dwoma łukami kołowymi o różnej krzywiźnie.

W relacji do innych stycznych i łuków każda krzywa przejściowa jest łukiem do wewnątrz albo łukiem na zewnątrz.

Dwoma najczęściej stosowanymi przez inżynierów parametrami podczas projektowania i określania krzywych przejściowych są L (długość krzywej przejściowej) i R (promień łuku kołowego).

Poniższa ilustracja przedstawia różne parametry krzywych przejściowych:

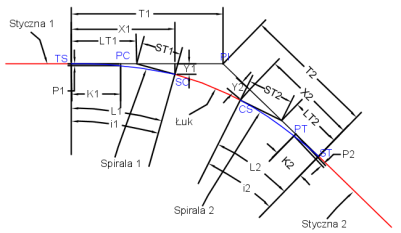
Parametr krzywej przejściowej	Opis
i1	Środkowy kąt łuku L1 krzywej przejściowej, który jest kątem krzywej przejściowej.
i2	Środkowy kąt łuku L2 krzywej przejściowej, który jest kątem krzywej przejściowej.
T1	Całkowita długość stycznej od PP do TS.
T2	Całkowita długość stycznej od PP do ST.
X1	Długość stycznej od TS, w SC.
X2	Długość stycznej od ST, w CS.
Y1	Odległość odsunięcia stycznej od TS, w SC.
Y2	Odległość odsunięcia stycznej od ST, w CS.
P1	Odsunięcie stycznej początkowej w stronę PS łuku przesuniętego.
P2	Odsunięcie stycznej początkowej od PT łuku przesuniętego.
K1	Wartość odciętej przesuniętego PC w odniesieniu do TS.
K2	Wartość odciętej przesuniętego PT w odniesieniu do ST.
LT1	Krzywa wyjściowa długiej stycznej.
LT2	Krzywa wyjściowa długiej stycznej.
ST1	Krzywa wyjściowa krótkiej stycznej.
ST2	Krzywa wyjściowa krótkiej stycznej.
	Inne parametry krzywej przejściowej
A1	Wartość A jest równa pierwiastkowi kwadratowemu długości krzywej przejściowej, pomnożonemu przez promień. Miara płaskości krzywej przejściowej.
A2	Wartość A jest równa pierwiastkowi kwadratowemu długości krzywej przejściowej, pomnożonemu przez promień. Miara płaskości krzywej przejściowej.

Wzór

krzywa złożona

Krzywe złożone umożliwiają przejście między dwoma łukami kołowymi o różnych promieniach. Tak jak w przypadku krzywej prostej, ta krzywa umożliwia zachowanie ciągłości funkcji krzywizny i stanowi sposób gładkiej przechyłki przejścia przed łukiem.

klotoida

Program AutoCAD Civil 3D obsługuje kilka typów krzywych przejściowych; klotoida jest najczęściej stosowanym typem krzywej przejściowej. Klotoida jest stosowana na całym świecie w projektach autostrad i linii kolejowych.

Zbadana po raz pierwszy przez szwajcarskiego matematyka Leonarda Eulera, funkcja krzywizny klotoidy to funkcja liniowa, której krzywizna w miejscu zetknięcia ze styczną wynosi zero (0), w funkcji długości. Następnie krzywizna rośnie liniowo, aż do zrównania z sąsiednim łukiem w punkcie zetknięcia krzywej przejściowej i łuku.

Tego rodzaju linia trasowania zapewnia ciągłość funkcji pozycji i jej pierwszej pochodnej (lokalny azymut), tak jak w przypadku stycznej i łuku w punkcie krzywizny (PC). Jednak inaczej niż w przypadku łuku prostego, zachowana jest także ciągłość drugiej pochodnej (krzywizna lokalna), co staje się szczególnie ważne przy wyższych prędkościach.

Wzór

Klotoida jest wyrażana wzorem:

Płaskość krzywej przejściowej:

Całkowity kąt wyznaczony przez krzywą przejściową:

Długość stycznej od punktu Styczna-Łuk w punkcie Styczna-Krzywa przejściowa:

Odległość odsunięcia łuku stycznej od punktu Styczna-Łuk w punkcie Krzywa przejściowa-Łuk:

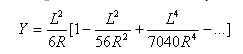
Krzywa Blossa

Zamiast klotoidy jako przejście można zastosować krzywą Blossa z parabolą piątego stopnia. Krzywa przejściowa ma przewagę nad klotoidą, ponieważ przesunięcie P jest mniejsze i dlatego przejście jest dłuższe, przy większym przedłużeniu (K) krzywej przejściowej. Ten czynnik ma znaczenie w projektach kolejowych.

Wzór

Krzywą Blossa można wyrazić następującym wzorem:

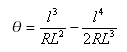
Inne wyrażenia:

Długość stycznej od punktu Styczna-Łuk w punkcie Styczna-Krzywa przejściowa:

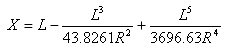
Odległość odsunięcia łuku stycznej od punktu Styczna-Łuk w punkcie Krzywa przejściowa-Łuk:

Krzywe sinusoidalne

Krzywe sinusoidalne przedstawiają stały przebieg zakrzywienia i można je stosować do przejść ugięć stycznych z przedziału od 0 do 90 stopni. Krzywe sinusoidalne nie są jednak powszechnie stosowane, ponieważ są one bardziej strome niż krzywe „rzeczywiste”, i z tego względu są też trudniejsze do ujęcia w tabele oraz do kontrolowania.

Wzór

Krzywe sinusoidalne można wyrazić następującym wzorem:

Po zróżnicowaniu za pomocą symbolu l otrzymywane jest równanie l/r, gdzie r stanowi promień krzywizny w danym punkcie:

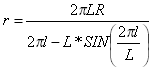
Łuk styczny w postaci połowy sinusoidy zanikającej

Ten rodzaj równania jest często stosowany w projektach linii kolejowych w Japonii. Łuk jest bardzo użyteczny, jeśli konieczne jest wydajne przejście krzywizny dla małych kątów odchyleń (w odniesieniu do dynamiki pojazdu).

Wzór

Łuki styczne w postaci połowy sinusoidy zanikającej mogą być wyrażane następującymi wzorami:

gdzie i x stanowią odległość od początku do dowolnego punktu na łuku, mierzoną wzdłuż (rozszerzonej) stycznej początkowej; X stanowi sumaryczną wartość X na końcu krzywej przejściowej.

Inne wyrażenia:

Długość stycznej od punktu Styczna-Łuk w punkcie Styczna-Krzywa przejściowa:

Odległość odsunięcia łuku stycznej od punktu Styczna-Łuk w punkcie Krzywa przejściowa-Łuk:

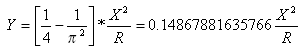
Krzywa sześcienna (JP)

Krzywa przejściowa została opracowana z myślą o wymaganiach inżynierów w Japonii. Utworzono określoną liczbę aproksymacji klotoidy przeznaczonych do stosowania w sytuacjach z małym kątem ugięcia lub dużym promieniem. Jedna z tych aproksymacji, stosowana w Japonii, to krzywa sześcienna (JP).

Wzór

Krzywa sześcienna (JP) jest definiowana wzorem:

Gdzie X = długość stycznej od punktu styczna-krzywa przejściowa w punkcie krzywa przejściowa-łuk

Ten wzór można również wyrazić w następujący sposób:

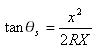
Gdzie jest środkowym kątem krzywej przejściowej (i1 oraz i2 na rysunku)

Inne wyrażenia:

Długość stycznej od punktu Styczna-Łuk w punkcie Styczna-Krzywa przejściowa:

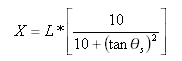
Odległość odsunięcia łuku stycznej od punktu Styczna-Łuk w punkcie Krzywa przejściowa-Łuk:

Parabole sześcienne

Parabole sześcienne zbiegają się mniej gwałtownie niż krzywe sześcienne, dzięki czemu są często stosowane w projektowaniu linii kolejowych i autostrad. Pomimo tego, że parabole sześcienne są mniej dokładne niż krzywe sześcienne, są jednak częściej stosowane przez inżynierów kolejowych i drogowych, ponieważ można je wyrazić za pomocą współrzędnych kartezjańskich i łatwo przedstawić je w terenie.

Wzór

Gdy -> zero -> można założyć, że cos = l, to x = l.

Co więcej, jeśli założone zostanie, że sin = , to

x = l i Suma_X = (w przybliżeniu) L

Zastosowanie przybliżenia ułatwia otrzymanie poniższego równania:

Pozostałe parametry pozostają takie same, jak w przypadku klotoidy.

Promień minimalny paraboli sześciennej

W dowolnym punkcie paraboli sześciennej promień wynosi:

Parabola sześcienna osiąga min. r w:

Więc

Promień paraboli sześciennej zmniejsza się od nieskończoności do przy kącie 24 stopnie 5 minut 41 sekund i od tego miejsca zaczyna ponownie rosnąć. Z tego względu parabole sześcienne są bezużyteczne przy zakrzywieniach większych niż 24 stopnie.

Krzywe przejściowe czwartego stopnia (krzywe przejściowe Schramma)

Krzywe przejściowe czwartego stopnia (krzywe przejściowe Schramma) mają niewielkie wartości przyspieszenia pionowego. Zawierają one dwie parabole drugiego stopnia, których promienie zmieniają się wraz z funkcją długości łuku.

Podstawowy wzór łuku

Krzywizna pierwszej paraboli:

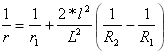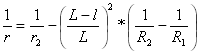dla